La estadística es una disciplina fundamental que permite la recopilación, análisis e interpretación de datos para la toma de decisiones informadas. Existen dos tipos principales de estadísticas:
La descriptiva, que se encarga de resumir y organizar datos para describir sus características principales, y la inferencial, que utiliza muestras de datos para hacer predicciones o inferencias sobre una población más amplia.

Comprender los diferentes tipos de estadísticas es esencial para aplicar correctamente sus métodos en diversas áreas del conocimiento. ¡Vamos a verlos con más detalle!

Tipos principales de estadística
Como hemos avanzado justo arriba, los dos principales tipos de estadística son la descriptiva y la inferencial. Descubre, a continuación, las diferencias entre ambas, y en qué casos es mejor emplear una u otra en un estudio estadístico.
Estadística descriptiva
"La estadística descriptiva es un conjunto de técnicas numéricas y gráficas para describir y analizar un grupo de datos, sin extraer conclusiones (inferencias) sobre la población a la que pertenecen", explica la Universidad de Santiago de Compostela 1.

Su objetivo es, añade la misma fuente, como "en cualquier análisis estadístico", "extraer conclusiones sobre un colectivo de interés denominado población".
Antes de continuar, vamos a ver algunos conceptos importantes que nos ayudarán a comprender mejor todo lo que ahondaremos después 1.⬇️
🔹 Población: un conjunto de individuos sobre el que se quiere extraer alguna conclusión.
🔹 Individuo: es cada uno de los elementos que forman la población.
🔹 Muestra: es un subconjunto representativo de la población.
En este tipo de estadísticas descriptivas, existen unas herramientas y técnicas comunes para analizar y extraer la información. Las principales son:
Medidas de tendencia central
🔹 Según explica la Universidad Internacional de La Rioja 2, este tipo de medidas resumen un conjunto de datos en uno solo, para simplificar su análisis.
Según las definiciones de la enciclopedia económica Economipedia 3, son las siguientes:
- La media: representa el valor promedio de un conjunto de datos; dicho valor resume el conjunto, y se obtiene sumando cada uno de los valores y dividiendo el resultado entre el número total de valores. ➡️Ejemplo: la media de 10 y 20 es 15 porque 10+20/2 da como resultado 15.
- La mediana: "divide una lista ordenada en dos partes iguales", y es el valor que está justo en la mitad del conjunto de datos.
- Y la moda: es el valor que más se repite de ese conjunto de datos.
Medidas de dispersión
Estas son las que miden si los datos son homogéneos o dispersos y en qué grado.
- La desviación típica: como explica la misma fuente, esta nos indica "cuánto se alejan, de media, los datos respecto a su valor medio o promedio". O, dicho de otro modo: "si tienes varios datos y quieres saber si están todos más o menos cerca del promedio o si, por el contrario, están muy repartidos".
- Y la varianza: nos indica cómo de alejados están los datos de un conjunto de su media.
➡️ Ejemplo práctico de aplicación de las medidas de tendencia central: las notas de Matemáticas de una clase:
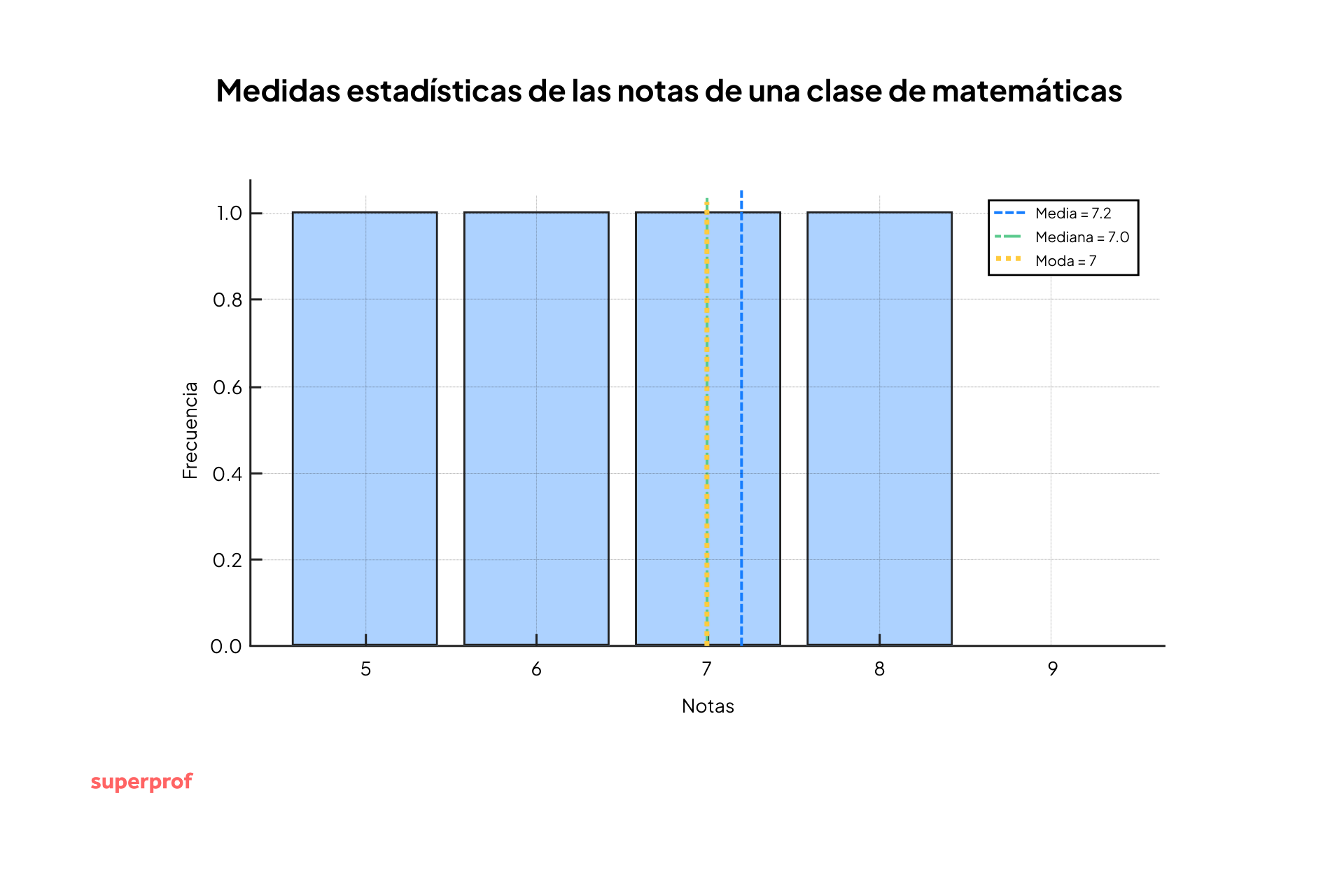
- Media: es la suma de todas las notas, dividida entre el número de alumnos y alumnas. Si las notas son 5, 6, 7, 8 y 10, la media es (5+6+7+8+10)/5 = 7.2.
- Mediana: es la nota que está en medio de la lista. Con las mismas notas, 5, 6, 7, 8, 10, la mediana es 7, lo que quiere decir que la mitad de la clase tiene más de un 7 de nota, y la otra mitad menos.
- Moda: es la nota que más se repite. Si las notas fuesen 5, 6, 7, 7, 8, 10, la moda sería 7.
- Desviación típica: mide cuánto se alejan las notas de la media.
- Varianza: sirve también para conocer la dispersión de los datos, pero de un modo más técnico. Si hay más varianza, hay más desigualdad en el éxito académico de los alumnos y alumnas de una clase.
📈 Te puede interesar: descubre qué son las variables estadísticas y por qué son la base de esta disciplina. ¡Te contamos todo lo que necesitas saber para empezar a estudiar!

Estadística inferencial
🔹A diferencia de la estadística descriptiva, que describe, la inferencial "es la parte de la Estadística que trata las condiciones bajo las cuales las inferencias extraídas a partir de una muestra son válidas para extraer conclusiones sobre la población de interés" 1.
Precisamente extraer conclusiones es el objetivo de este tipo de estadística, así como hacer predicciones, en base a una muestra, de una población en general. Este tipo de conclusiones se obtienen, principalmente, a través de los siguientes métodos que definiremos, según explica Francisco M. Ocaña Peinado, del Departamento de Estadística e Investigación Operativa de la Universidad de Granada 4:
- Estimación: consiste en "pronosticar el valor de un parámetro desconocido a partir del valor que nos proporciona un estadístico de la muestra". ➡️ Ejemplo: "Se estima que el porcentaje de personas con obesidad en una población es del 14.3%".
- Intervalos de confianza: "consiste en atribuir al parámetro desconocido un intervalo de valores entre los que se espera que pueda encontrarse el valor del mismo con una probabilidad alta y conocida". ➡️ Ejemplo: "Se estima que el peso medio de una población infantil está comprendido entre 21.3 kg y 23.3 kg con una confianza del 99%".
- Pruebas de hipótesis: "Dada una afirmación acerca de una población, determinar si puede rechazarse o no dicha afirmación a partir de los datos dela muestra". ➡️ Ejemplo: "La obesidad en poblaciones infantiles afecta en mayor proporción a niños que a niñas".
➡️ Ejemplo práctico de aplicación de las medidas inferenciales: las notas de Matemáticas de una clase: para que los conceptos que hemos visto más arriba queden más claros, retomamos el ejemplo de las notas de una clase de Matemáticas. ¡Lo resumimos en la siguiente tabla!👇
| Concepto | Qué hace | Ejemplo |
|---|---|---|
| Estimación | Usa la muestra para calcular un valor representativo de la población. | Se estima que la media de la clase es de 7.5. |
| Intervalo de confianza | Da un rango posible donde se encuentra el valor real. | La media está entre 7.1 y 7.9 con un 95% de confianza. |
| Prueba de hipótesis | Permite aceptar o rechazar una suposición sobre la población. | Se rechaza la hipótesis de que la media sea 7. |
Otras ramas de la estadística
Hasta ahora, hemos visto los tipos de estadística según su objetivo y la metodología utilizada. Pero también se puede clasificar en función de la rama para la que se emplee, como las ciencias de la salud, los análisis económicos o las ciencias sociales. ¡Como verás, es fundamental en estas áreas vitales para la vida!
Bioestadística
Según la Universidad Europea 5, la bioestadística es "la rama que se encarga de aplicar los principios, métodos y técnicas de la estadística a la biología y las ciencias de la salud". Es decir, que "permite recopilar, organizar, analizar e interpretar los datos de salud para extraer conclusiones y facilitar la toma de decisiones en el ámbito sanitario".
Para que resulte más sencillo de comprender, podemos resumir diciendo que llamamos bioestadística al estudio de la Estadística en Ciencias de la Salud. La misma fuente resalta su importancia, puesto que "la mayoría de las decisiones clínicas se apoyan en análisis estadísticos".
- ➡️ Ejemplo: se usaría la bioestadística para conocer la efectividad de un medicamento.
Otro ejemplo muy representativo y que, seguramente ha escuchado o leído en las noticias, es por ejemplo, la Encuesta de Salud del INE, Instituto Nacional de Estadística, que presenta cada año sus conclusiones aplicando todos los conocimientos que hemos ido explicando a lo largo de estas líneas.
Estadística económica
La estadística económica es la rama de la estadística que recopila, ordena y analiza datos relacionados con la actividad económica, con el objetivo de entenderla mejor, así como para obtener información que ayude en la toma de decisiones.
Y esto lo hace a través de análisis económicos y financieros. Dicho de otro modo, el estudio de estos datos permite comprender la economía, por ejemplo de un país, y tomar decisiones en función de los mismos.
Como explica el INE 6, esta información es de gran utilidad para:
- Los Gobiernos, que necesitan información sobre la economía para tomar decisiones al respecto.
- La ciudadanía, pues también les permite tener información sobre la eficacia y el desempeño de los Gobiernos.
- Las empresas, que "necesitan información sobre la evolución de sus productos y los de la competencia en el mercado, sobre la economía, la población y las tendencias sociales", que le "permitirá tomar decisiones sobre políticas de marketing de sus productos, dónde abrir nuevas oficinas y locales, localización de almacenes y fábricas, etc".
Estadística social
Por último, e íntimamente relacionada con las dos anteriores, está la estadística social, que se aplica en los estudios sociológicos y demográficos. Esta rama de la estadística recoge y analiza datos sobre la sociedad y cómo se comporta.
Serían, por ejemplo, los análisis demográficos de la población, acceso a la educación y nivel educativo, empleo y desempleo, hábitos de consumo, etc.
Bioestadística
➡️ Se aplica a la biología, medicina y salud.
Estadística económica
➡️Estudia los fenómenos económicos y financieros.
Estadística social
➡️ Estudia fenómenos sociales y colectivos.
La estadística no solo es una ciencia en sí, sino que también es una importante herramienta para otras ramas de la ciencia, por eso es importante conocer los diferentes tipos de estadísticas, interpretar los datos estadísticos y aplicarlo de manera correcta. ¡De ello puede depender la fiabilidad o validez de un estudio, y no es ninguna tontería!
Bibliografía
- Introducción, 1., Generales, 2. Conceptos, De frecuencias, 3. Distribuciones, Gráficas, 4. Representaciones, & Posición, 5. Medidas Características: (s/f). Tema 1. Estadística Descriptiva. Usc.es. Recuperado el 7 de octubre de 2025, de http://eio.usc.es/eipc1/BASE/BASEMASTER/FORMULARIOS-PHP-DPTO/MATERIALES/Mat_G2021103104_EstadisticaTema1.pdf
- ¿Qué son las medidas de tendencia central y para qué sirven? (2025, julio 2). Universidad Internacional de La Rioja. https://colombia.unir.net/actualidad-unir/medidas-tendencia-central/
- Pareja, C. (2019, noviembre 15). Estadística descriptiva: Qué es, tipos y ejemplos. Economipedia. https://economipedia.com/definiciones/estadistica-descriptiva.html
- De hipótesis, E. y. C. (s/f). ANÁLISIS DE VARIABLES RELACIONADAS CON LA DOCENCIA E INVESTIGACIÓN EN LA FAC. FARMACIA. Ugr.es. Recuperado el 8 de octubre de 2025, de https://www.ugr.es/~fmocan/MATERIALES%20CURSO/ESTIMACION%20Y%20CONTRASTES.pdf
- Bioestadística: ¿qué es y cómo se utiliza en las ciencias de la salud? (2022, noviembre 11). Universidad Europea; Universidad Europea | Universidad presencial (Madrid, Valencia, Alicante, Canarias, Málaga) y Online. https://universidadeuropea.com/blog/que-es-bioestadistica/
- (S/f-d). Ine.es. Recuperado el 1 de octubre de 2025, de https://www.ine.es/ine/oposiciones/temario_2021/manual_basico_estadistica.pdf
Resumir con IA:















