Los datos estadísticos son valores numéricos obtenidos mediante la observación y el análisis de fenómenos específicos, utilizados para describir, interpretar y predecir comportamientos o tendencias en diversos ámbitos.
Los datos estadísticos son fundamentales en diversos campos, desde la investigación científica hasta la toma de decisiones empresariales. Este artículo explora qué son, su relevancia y cómo se aplican en diferentes contextos. ¡Vamos punto por punto!📈

¿Qué son los datos estadísticos?
Según el Diccionario de Matemáticas de Superprof 1, "un dato estadístico es cada uno de los valores que se ha obtenido al realizar un estudio estadístico".
🔹Un ejemplo: "Si lanzamos una moneda al aire 5 veces obtenemos 5 datos: cara, cara, cruz, cara, cruz".
El concepto "datos estadísticos" se forma con la suma de dos conceptos que, a su vez, tienen significado propio:
- Por un lado, "datos", que viene del latín "datum" y que significa "lo dado". Según la Real Academia de la Lengua Española, los datos son "información sobre algo concreto que permite su conocimiento exacto o sirve para deducir las consecuencias derivadas de un hecho".
- Y, por otro, "estadísticos", que también viene de la palabra en latín "status" cuyo significado es "estado" o "situación".
Por lo tanto, tenemos por un lado los datos, es decir, una información; y por otro, la vinculación de dichos datos a la estadística.
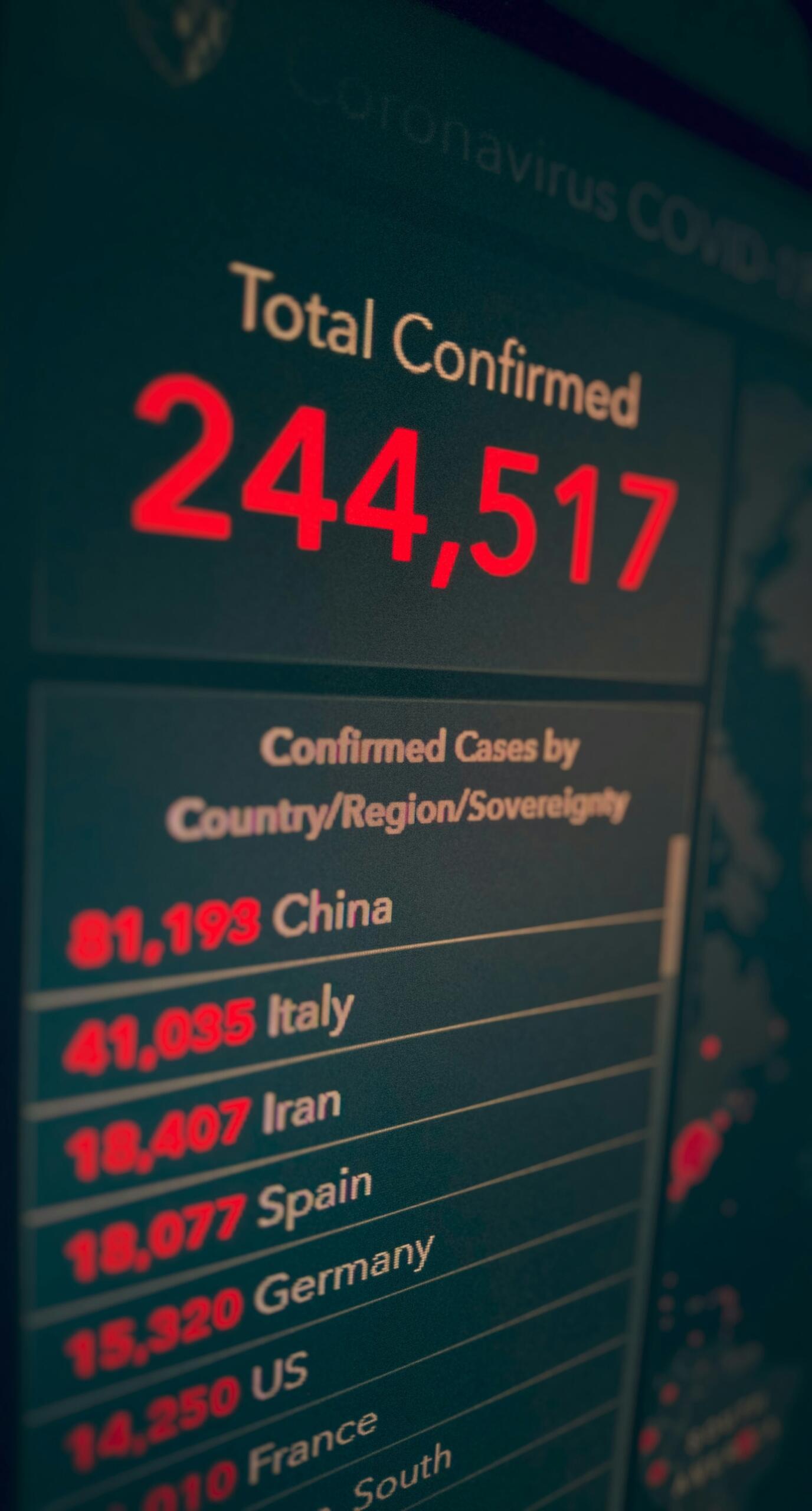
Según de nuevo la RAE 2, la estadística es "el estudio científico que tiene por objeto la recopilación, clasificación y análisis de los datos numéricos concernientes a determinados fenómenos, así como la obtención de conclusiones a partir de ellos".
Los datos estadísticos tienen como características principales que son objetivos, cuantificables y relevantes. Aunque, esto depende, claro está, de cómo se haga el análisis de los mismos. Es decir, el dato en sí no tiene un significado como tal: he tirado la moneda al aire y ha salido cara.
Sin embargo, el análisis estadístico de estos datos nos puede facilitar alguna conclusión: hay un X% de veces que sale cara si tiras una moneda al aire.
¿Cuándo se utilizan los datos estadísticos?
Según el Instituto Nacional de Estadística 3, los datos estadísticos se usan "como información de ayuda para la toma de decisiones o, simplemente, para estar informado/a"; y, por ejemplo, los vemos en los medios de comunicación, según la misma fuente en, cuando se habla de:
- Los datos de desempleo
- Los precios de consumo
- Las encuestas electorales
- Los sondeos de opinión
- Las cifras de audiencias de un programa de televisión
- El grado de satisfacción de compra de un producto
- El rendimiento de las campañas publicitarias, y un largo etcétera.
Viendo estos ejemplos habrás llegado, seguramente, a la conclusión de que, aunque los datos estadísticos se presuponen objetivos, también son interpretables. Si no ¿cómo es posible que las encuestas electorales sean ventajosas para el partido que las interpreta o que dos programas de televisión sean líderes de audiencia?😉
📈 Te puede interesar: las variables estadísticas son la base de esta disciplina. ¡Te contamos todo lo que necesitas saber para empezar a estudiar!
Importancia de los datos estadísticos
Solo viendo algunos de los ejemplos de más arriba, es evidente la importancia que pueden tener los datos estadísticos en distintos aspectos: desde la retirada de un programa de televisión por falta de audiencia; hasta las medidas en políticas de empleo de un gobierno según los datos de desempleo. ¡No es ninguna trivialidad!
En la investigación científica
La estadística es una de las herramientas clave de la investigación científica, ya que a través de los datos estadísticos se pueden fundamentar hipótesis y validar resultados en estudios científicos. En todos los ámbitos de las ciencias, desde las formales hasta las sociales, se utilizan los datos estadísticos. Dicho de otro modo, la Estadística es en sí misma una ciencia, que acompaña al resto de las ciencias.
La docente e investigadora de la Universidad de Jaén, UJA, lo explica de este modo 4:
"Lo bonito de las Matemáticas es que establece modelos generales. Con un mismo modelo podemos explicar situaciones diversas. Utilizamos técnicas estadísticas para identificar sesgos, analizar la calidad de las muestras y evaluar los resultados".

Y añade: "Nosotros escuchamos a los datos y con las hipótesis que planteamos, decidimos si se pueden considerar válidas o no, en función de lo que los datos digan, pero siempre con cautela".
En la toma de decisiones empresariales
El uso de los datos estadísticos es necesario para implementar estrategias de mercado, hacer análisis financieros o mejorar los procesos en el ámbito empresarial.
Como explica de nuevo el INE, "las empresas necesitan información sobre la evolución de sus productos y los de la competencia en el mercado, sobre la economía, la población y las tendencias sociales.
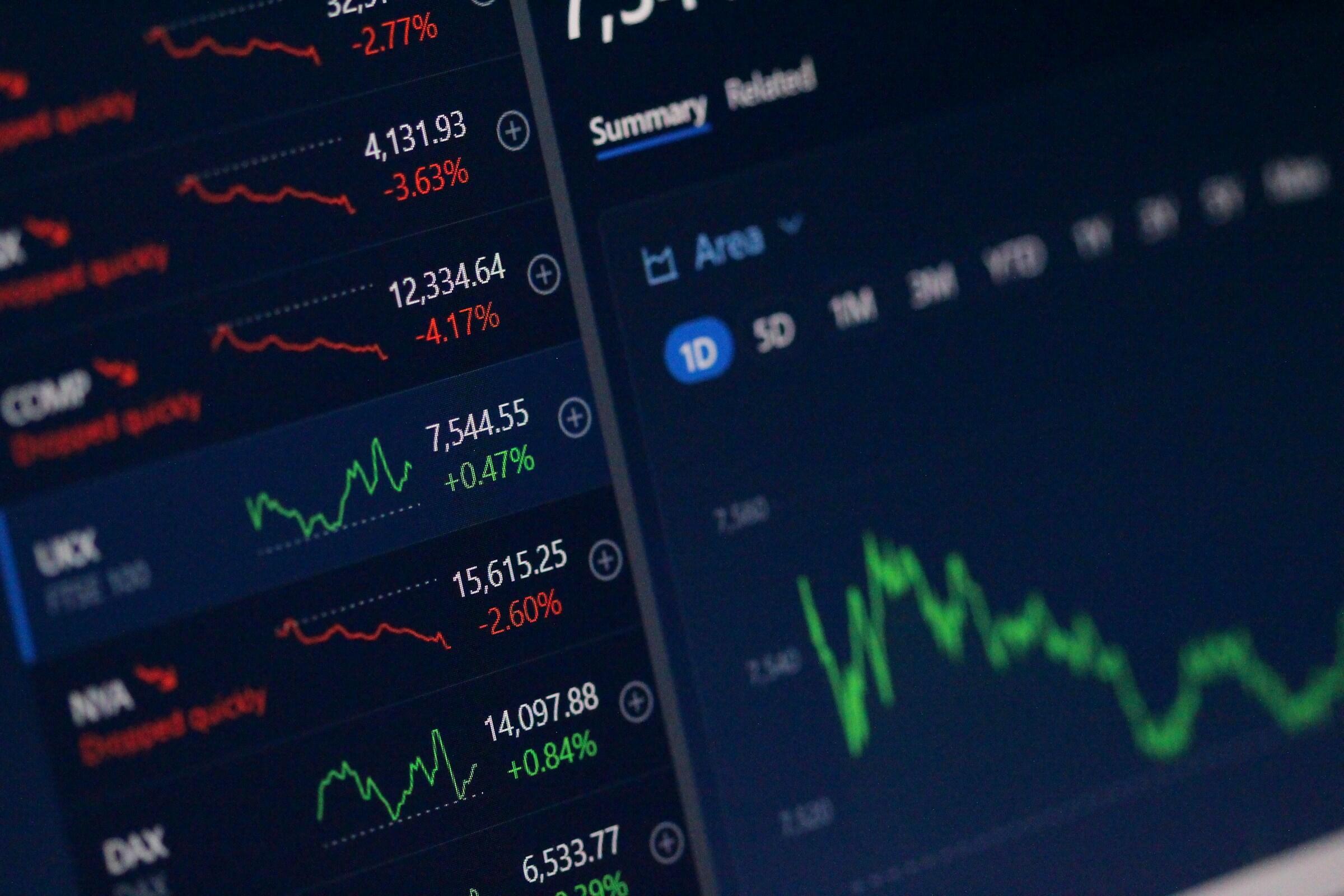
Ello les permitirá tomar decisiones sobre políticas de marketing de sus productos, dónde abrir nuevas oficinas y locales, localización de almacenes y fábricas. etc".
A lo que la también investigadora docente de la UJA Rosa María Martínez añade que "cada día, las empresas están más convencidas de que necesitan analistas. Muchas veces, buscan a esos analistas en nuestro alumnado de Estadística y de Matemáticas. Hoy en día, en el mundo en el que vivimos, todo se basa en interpretar los datos para intentar sacar el mejor partido de ello. Las empresas buscan las tendencias, las preferencias de su público y de sus clientes".
En políticas públicas
Por último, y tal vez más importante, los datos estadísticos también se aplican en la formulación y evaluación de las políticas gubernamentales. Como decíamos en el ejemplo de más arriba: usar los datos estadísticos del desempleo para impulsar políticas de empleo.
El INE complementa lo explica apelando a que los gobiernos, tanto nacionales como autonómicos o locales, necesita tener información "sobre la población, la economía y otros asuntos que le permita tomar decisiones sobre localización de servicios, tasas impositivas, ayudas sociales, etc".
Pero no solo eso, sino que la importancia está también a la inversa: "los datos estadísticos también permiten a los ciudadanos disponer de información sobre la actuación y el desempeño de sus gobernantes". ¡Son una herramienta útil para toda la ciudadanía!

Tipos de datos estadísticos
De acuerdo, la estadística trabaja con datos, pero igual que hay distintos tipos de estadísticas, también hay diferentes tipos: datos cualitativos y datos cuantitativos. Es un dato, por ejemplo, que en una cochera hay 200 coches; y también que algunos de esos coches son rojos. ¿Vas viendo la diferencia?
Datos cuantitativos
Los datos cuantitativos son datos numéricos, que representan cantidades que son medibles. Siguiendo con el ejemplo anterior: ➡️ serían los 200 coches.
Datos cualitativos
Como su propio nombre indica, los datos cualitativos representan cualidades, categorías o características. Para analizarlos estadísticamente hay que cuantificarlos, otorgarles un número, por así decirlo, para poder realizar operaciones, porcentajes, etc.
- ➡️ Por ejemplo: los coches rojos de los que hablábamos antes, son 100. O lo que es lo mismo, el 50% de los coches son rojos.
¡Vamos a ver algunos ejemplos más!
Datos cuantitativos
Edad
Altura
Peso
Número de hijos
Ingresos mensuales
Temperatura
Dólares
Datos cualitativos
Color de ojos
Estado civil
Marca de un coche
Aprobado/suspenso
Nacionalidad
Comida preferida
Medio de transporte habitual
¿Cómo se pueden cuantificar los cualitativos? ➡️ 10 personas tienen los ojos azules; el 50% de los encuestados están casados; o el metro es utilizado por X número de personas al día. ¡Ahora es más sencillo ver la diferencia, verdad!
Los datos estadísticos son valores numéricos obtenidos mediante métodos sistemáticos de recolección y análisis, utilizados para describir y predecir fenómenos específicos. En cambio, los datos comunes pueden ser cualquier tipo de información sin un proceso estructurado de análisis.
Métodos de recolección de datos estadísticos
Una vez que hemos visto los tipos de datos estadísticos que existen y la diferencia que hay entre ellos, vamos a detenernos en saber cómo se obtienen. Fundamentalmente hay tres maneras:
Encuestas y cuestionarios
Técnicas para obtener datos directamente de los sujetos de estudio.
- Ejemplo: ➡️Las que hace el mencionado Instituto Nacional de Estadística para, por ejemplo, analizar el turismo y saber dónde pasan los españoles y españolas las vacaciones. También para conocer hábitos de consumo en el hogar; o de lectura, entre otros. Serían también las encuestas de intención de voto en las elecciones.
Observación directa
Este método recopila los datos directamente mediante la observación sistemática de fenómenos.
- Ejemplo: ➡️ cuando el Metro de Madrid, una persona cuenta cuantas personas han entrado en la estación o subido a una línea; o cuando se contabilizan, por ejemplo, las bicicletas que pasan durante un día por una calle concreta.
Experimentos Controlados
Por último, los experimentos controlados consisten en diseñar y ejecutar experimentos para obtener datos bajo condiciones controladas para analizar o estudiar un fenómeno o suceso.
- Ejemplo: ➡️cuando se hace un ensayo clínico sobre los efectos de una medicación; o cuando se estudia a un grupo de personas que toman una alimentación X en comparación a una alimentación Y. También los estudios de mercado que hacen algunas marcas con un grupo de personas que prueban un nuevo producto para conocer el grado de satisfacción, entre otros ejemplos.
Análisis e interpretación de datos estadísticos
Igual que es importante recopilar los datos, lo también saber analizarlos para poder elaborar un estudio estadístico. Para ello, vamos a repasar algunos conceptos clave:
Medidas de tendencia central
Las medidas de tendencia central son, según explica la UNIR 5 maneras de medir que resumen un conjunto de datos "en un solo valor" lo que "simplifica el análisis de todo un bloque de información y proporciona una visión generalizada sobre el mismo". Son, por ejemplo:
- La media: es el valor medio de un conjunto de datos. Se calcula sumando todos los valores de ese conjunto de datos y dividiendo por el número total. Se usa, por ejemplo, para calcular la nota media de un alumno/a. ➡️ Si ha sacado 5 en matemáticas, 6 en inglés, 7 en lengua, 7 en Historia y 10 en Filosofía: se suma 5+6+7+7+10 y se divide entre cinco.
- La mediana: es el punto central de un conjunto de datos. El valor que está en el medio, por así decirlo. ➡️ En el ejemplo anterior, la mediana sería el 7.
- Y la moda: sería el valor más repetido del conjunto de datos. ➡️ En el ejemplo anterior, el 7.
Medidas de dispersión
Estas sirven para saber cómo de homogéneos o dispersos son esos datos. Los conceptos que debes conocer son:
- Varianza: calcula cuánto se desvían o alejan los datos respecto a la media. Necesitamos la varianza para calcular la desviación estándar.
- Desviación estándar: es la raíz cuadrada de la varianza. Y permite conocer la dispersión de los datos de la media en la misma unidad de medida, como kilos, metros, etc.
- Y rango: es la diferencia entre el valor más alto y el más bajo. ➡️ El 10 de Historia, menos el 5 de Matemáticas.
Representación gráfica de datos

Por último, la representación gráfica de datos usa gráficos y diagramas para visualizar los datos estadísticos de manera más visual y efectiva. No se refiere a la manera de obtener los datos, sino a cómo representarlos.
| Concepto | Definición | Ejemplo de cálculo con datos (5, 7, 8, 10, 10, 12, 15) | Interpretación |
|---|---|---|---|
| Media | Promedio aritmético de los valores. | (5+7+8+10+10+12+15) ÷ 7 = 9,57 | Valor “central” que representa a todo el conjunto. |
| Mediana | Valor central cuando los datos están ordenados. | Datos ordenados: 5, 7, 8, 10, 10, 12, 15 → Mediana = 10 | La mitad de los datos está por debajo y la otra mitad por encima. |
| Moda | Valor que más se repite. | El número 10 aparece dos veces. | Indica el valor más frecuente. |
| Rango | Diferencia entre el valor máximo y mínimo. | 15 – 5 = 10 | Muestra la amplitud de los datos. |
| Varianza | Promedio de las desviaciones al cuadrado respecto a la media. | ≈ 9,81 | Indica cuánto varían los datos respecto a la media. |
| Desviación estándar | Raíz cuadrada de la varianza. | √9,81 ≈ 3,13 | Variación promedio respecto a la media. |
Como has podido comprobar, saber analizar los datos es algo que nos puede facilitar el día a día y la toma de decisiones documentadas. Gracias a los datos estadísticos se puede evaluar el rendimiento académico y, en consecuencia, diseñar políticas educativas; llevar a cabo análisis económicos, para prever cómo evolucionará el mercado; hacer estudios clínicos y epidemiológicos, etc. ¡Cosas tan y tan importantes!
Si te ha parecido interesante lo que has leído hasta aquí, te puede interesar profundizar en el análisis e interpretación de datos estadísticos consultando el recurso educativo de Ellistat sobre parámetros estadísticos de variabilidad. Y, por supuesto, puedes aprender estadística con Superprof. ¡Será un aprendizaje a tu medida y en función de qué campos te interesen más!
Bibliografía
- dato estadístico - Diccionario de Matemáticas. (s/f). Diccionario de Matemáticas | Superprof. Recuperado el 1 de octubre de 2025, de https://www.superprof.es/diccionario/matematicas/estadistica/dato.html
- (S/f-c). Rae.es. Recuperado el 1 de octubre de 2025, de https://www.rae.es/diccionario-estudiante/estad%C3%ADstico
- (S/f-d). Ine.es. Recuperado el 1 de octubre de 2025, de https://www.ine.es/ine/oposiciones/temario_2021/manual_basico_estadistica.pdf
- Estadística y sus aplicaciones, en ‘Campus: Panel de Expert@s’, de UniRadio Jaén. (s/f). Ujaen.es. Recuperado el 1 de octubre de 2025, de https://diariodigital.ujaen.es/divulgacion-cientifica/estadistica-y-sus-aplicaciones-en-campus-panel-de-experts-de-uniradio-jaen
- ¿Qué son las medidas de tendencia central y para qué sirven? (2025, julio 2). Universidad Internacional de La Rioja. https://colombia.unir.net/actualidad-unir/medidas-tendencia-central/
Resumir con IA:















