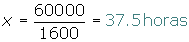La regla de tres es un procedimiento para calcular el valor de una cantidad comparándola con otras tres o más cantidades conocidas.

Regla de tres simple y directa

Se aplica une regla de 3 cuando dadas dos cantidades correspondientes a magnitudes directamente proporcionales, hay que calcular la cantidad de una de estas magnitudes correspondiente a una cantidad dada de la otra magnitud.

Explicaciones y ejemplos de regla de tres - 1

La regla de tres directa la aplicaremos cuando entre las magnitudes se establecen las relaciones:

A más Explicaciones y ejemplos de regla de tres - 2 más.

A menos Explicaciones y ejemplos de regla de tres - 3 menos.

Ejemplos de regla de 3

Un automóvil recorre 240 km en 3 horas. ¿Cuántos kilómetros habrá recorrido en 2 horas?

Son magnitudes directamente proporcionales, ya que a menos horas recorrerá menos kilómetros.

240 kmExplicaciones y ejemplos de regla de tres - 4 3 h

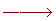
x   km  Explicaciones y ejemplos de regla de tres - 5 2 h

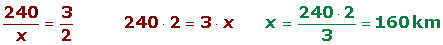
Explicaciones y ejemplos de regla de tres - 6

Ana compra 5 kg de patatas, si 2 kg cuestan 0.80 €, ¿cuánto pagará Ana?

Son magnitudes directamente proporcionales, ya que a más kilos, más euros.

2 kgExplicaciones y ejemplos de regla de tres - 7 0.80 €

5   kg  Explicaciones y ejemplos de regla de tres - 8x €

Explicaciones y ejemplos de regla de tres - 9

Regla de tres simple inversa

Consiste en que dadas dos cantidades correspondientes a magnitudes inversamente proporcionales, calcular la cantidad de una de estas magnitudes correspondiente a una cantidad dada de la otra magnitud.

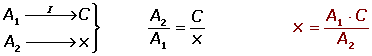
Explicaciones y ejemplos de regla de tres - 10

La regla de tres inversa la aplicaremos cuando entre las magnitudes se establecen las relaciones:

A más Explicaciones y ejemplos de regla de tres - 11 menos.

A menos Explicaciones y ejemplos de regla de tres - 12 más.

Ejemplo

Un grifo que mana 18 l de agua por minuto tarda 14 horas en llenar un depósito. ¿Cuánto tardaría si su caudal fuera de 7 l por minuto?

Son magnitudes inversamente proporcionales, ya que a menos litros por minuto tardará más en llenar el depósito.

18 l/min Explicaciones y ejemplos de regla de tres - 13 14 h

7 l/min   Explicaciones y ejemplos de regla de tres - 14    x h

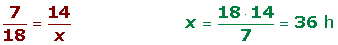
Explicaciones y ejemplos de regla de tres - 15

3 obreros construyen un muro en 12 horas, ¿cuánto tardarán en construirlo 6 obreros?

Son magnitudes inversamente proporcionales, ya que a más obreros tardarán menos horas.

3 obreros Explicaciones y ejemplos de regla de tres - 16 12 h

6 obreros  Explicaciones y ejemplos de regla de tres - 17    x h

Explicaciones y ejemplos de regla de tres - 18

La regla de tres compuesta se emplea cuando se relacionan tres o más magnitudes, de modo que a partir de las relaciones establecidas entre las magnitudes conocidas obtenemos la desconocida.

Una regla de 3 compuesta se compone de varias reglas de 3 simples aplicadas sucesivamente.

Como entre las magnitudes se pueden establecer relaciones de proporcionalidad directa o inversa, podemos distinguir tres casos de regla de tres compuesta:

Regla de tres compuesta directa

Explicaciones y ejemplos de regla de tres - 19

Ejemplo

Nueve grifos abiertos durante 10 horas diarias han consumido una cantidad de agua por valor de 20 €. Averiguar el precio del vertido de 15 grifos abiertos 12 horas durante los mismos días.

A más grifos, más euros Explicaciones y ejemplos de regla de tres - 20 Directa.

A más horas, más euros Explicaciones y ejemplos de regla de tres - 21 Directa.

9 grifos  Explicaciones y ejemplos de regla de tres - 22 10 horas Explicaciones y ejemplos de regla de tres - 23 20 €

15 grifos Explicaciones y ejemplos de regla de tres - 24 12 horas  Explicaciones y ejemplos de regla de tres - 25   x €

Explicaciones y ejemplos de regla de tres - 26

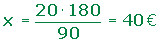
Explicaciones y ejemplos de regla de tres - 27

Regla de tres compuesta inversa

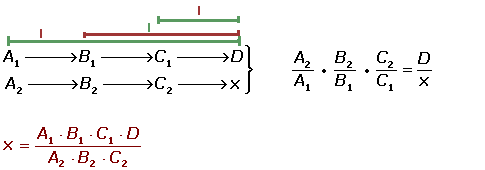
Explicaciones y ejemplos de regla de tres - 28

Ejemplo

5 obreros trabajando, trabajando 6 horas diarias construyen un muro en 2 días. ¿Cuánto tardarán 4 obreros trabajando 7 horas diarias?

A menos obreros, más díasExplicaciones y ejemplos de regla de tres - 29 Inversa.

A más horas, menos díasExplicaciones y ejemplos de regla de tres - 30 Inversa.

5 obreros  Explicaciones y ejemplos de regla de tres - 31 6 horas Explicaciones y ejemplos de regla de tres - 32 2 días

4 obreros Explicaciones y ejemplos de regla de tres - 33 7 horas  Explicaciones y ejemplos de regla de tres - 34   x días

Explicaciones y ejemplos de regla de tres - 35

Regla de tres compuesta mixta

Explicaciones y ejemplos de regla de tres - 36

Ejemplo

Si 8 obreros realizan en 9 días trabajando a razón de 6 horas por día un muro de 30 m. ¿Cuántos días necesitarán 10 obreros trabajando 8 horas diarias para realizar los 50 m de muro que faltan?

A más obreros, menos díasExplicaciones y ejemplos de regla de tres - 37 Inversa.

A más horas, menos díasExplicaciones y ejemplos de regla de tres - 38 Inversa.

A más metros, más días Explicaciones y ejemplos de regla de tres - 39 Directa.

8 obreros    Explicaciones y ejemplos de regla de tres - 40 9 días Explicaciones y ejemplos de regla de tres - 41 6 horas Explicaciones y ejemplos de regla de tres - 42 30 m

10 obreros Explicaciones y ejemplos de regla de tres - 43 x días Explicaciones y ejemplos de regla de tres - 44 8 horas Explicaciones y ejemplos de regla de tres - 45 50 m

Explicaciones y ejemplos de regla de tres - 46

11 obreros labran un campo rectangular de 220 m de largo y 48 de ancho en 6 días. ¿Cuántos obreros serán necesarios para labrar otro campo análogo de 300 m de largo por 56 m de ancho en cinco días?

220 · 48 m² Explicaciones y ejemplos de regla de tres - 47 6 días Explicaciones y ejemplos de regla de tres - 48 11 obreros

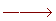
300 · 56 m² Explicaciones y ejemplos de regla de tres - 49 5 días Explicaciones y ejemplos de regla de tres - 50 x obreros

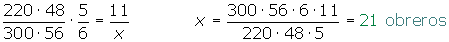
Explicaciones y ejemplos de regla de tres - 51

Seis grifos, tardan 10 horas en llenar un depósito de 400 m³ de capacidad. ¿Cuántas horas tardarán cuatro grifos en llenar 2 depósitos de 500 m³ cada uno?

6 grifos Explicaciones y ejemplos de regla de tres - 52 10 horas Explicaciones y ejemplos de regla de tres - 53 1 depósito Explicaciones y ejemplos de regla de tres - 54  400 m³

4 grifos Explicaciones y ejemplos de regla de tres - 55 x  horas   Explicaciones y ejemplos de regla de tres - 56 2 depósitos Explicaciones y ejemplos de regla de tres - 57 500 m³

Explicaciones y ejemplos de regla de tres - 58

Explicaciones y ejemplos de regla de tres - 59