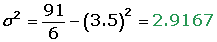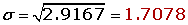La media de una distribución de probabilidad se denota por la letra griega µ (mu).

Explicaciones y ejemplos de parámetros de una distribución de probabilidad - 1

A la media también se le suele llamar valor esperado o esperanza matemática y se puede denotar como E(x).

Estos nombres tienen su origen en los juegos de azar y hacen referencia a la ganancia promedio esperada por un jugador cuando hace un gran número de apuestas.

Si la esperanza matemática es cero, E(x) = 0, el juego es equitativo, es decir, no existe ventaja ni para el jugador ni para la banca.

Varianza

La varianza y desviación típicade una distribución de probabilidad se denotan por la letra griega σ (sigma) : σ2 y σ.

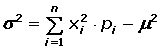
Explicaciones y ejemplos de parámetros de una distribución de probabilidad - 2

Desviación típica

Explicaciones y ejemplos de parámetros de una distribución de probabilidad - 3

Ejemplo

Calcular la esperanza matemática, la varianza, y la desviación típica, de la distribución de probabilidad de las puntuaciones obtenidas al lanzar un dado.

x p i x· p i x 2 ·pi
1 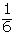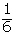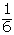Explicaciones y ejemplos de parámetros de una distribución de probabilidad - 4 Explicaciones y ejemplos de parámetros de una distribución de probabilidad - 5 Explicaciones y ejemplos de parámetros de una distribución de probabilidad - 6
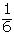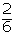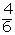2 Explicaciones y ejemplos de parámetros de una distribución de probabilidad - 7 Explicaciones y ejemplos de parámetros de una distribución de probabilidad - 8 Explicaciones y ejemplos de parámetros de una distribución de probabilidad - 9
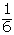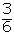3 Explicaciones y ejemplos de parámetros de una distribución de probabilidad - 10 Explicaciones y ejemplos de parámetros de una distribución de probabilidad - 11 Explicaciones y ejemplos de parámetros de una distribución de probabilidad - 12
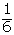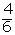4 Explicaciones y ejemplos de parámetros de una distribución de probabilidad - 13 Explicaciones y ejemplos de parámetros de una distribución de probabilidad - 14 Explicaciones y ejemplos de parámetros de una distribución de probabilidad - 15
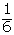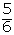5 Explicaciones y ejemplos de parámetros de una distribución de probabilidad - 16 Explicaciones y ejemplos de parámetros de una distribución de probabilidad - 17 Explicaciones y ejemplos de parámetros de una distribución de probabilidad - 18
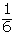6 Explicaciones y ejemplos de parámetros de una distribución de probabilidad - 19 1 6
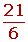Explicaciones y ejemplos de parámetros de una distribución de probabilidad - 20 Explicaciones y ejemplos de parámetros de una distribución de probabilidad - 21

Explicaciones y ejemplos de parámetros de una distribución de probabilidad - 22

Explicaciones y ejemplos de parámetros de una distribución de probabilidad - 23

Explicaciones y ejemplos de parámetros de una distribución de probabilidad - 24