Los fractales son estructuras geométricas que exhiben patrones auto-similares a diferentes escalas, desafiando las nociones tradicionales de dimensión y forma.
Desde su formalización por Benoît Mandelbrot en 1975, los fractales han fascinado tanto a matemáticos como a artistas, revelando la complejidad inherente en la naturaleza y en las construcciones humanas1.
Los fractales más famosos incluyen el Conjunto de Mandelbrot, el Triángulo de Sierpinski, la Curva de Koch y la Esponja de Menger. Estas estructuras destacan por su auto-similitud y complejidad infinita, encontrando aplicaciones en diversas áreas como la informática, la física y el arte.
Conjunto de Mandelbrot
El Conjunto de Mandelbrot es quizás el fractal más emblemático, definido por la iteración de la función compleja f(z) = z² + c. Su representación gráfica revela una estructura infinitamente compleja y auto-similar, con detalles que emergen a medida que se amplía la imagen2.
El procedimiento consiste en iterar esta función una y otra vez, comenzando desde z = 0, y observar si la secuencia permanece acotada o diverge al infinito.
Los valores de c para los cuales la secuencia no diverge conforman el Conjunto de Mandelbrot: el resultado, al representarse gráficamente, es una figura con un “cuerpo” principal y una infinidad de filamentos y espirales que se repiten a distintas escalas.
¿Por qué es tan importante el Mandelbrot set? 📐
- Autosimilitud infinita: al hacer zoom sobre sus bordes, aparecen estructuras similares a la figura completa.
- Complejidad desde reglas simples: una ecuación elemental genera una complejidad visual aparentemente infinita.
- Puente entre matemática y computación: su exploración masiva solo fue posible gracias al desarrollo de computadores.
Este fractal ha sido objeto de numerosos estudios y es considerado una piedra angular en la teoría de los fractales.
Este fractal cambió la forma en que los matemáticos entendían la relación entre simplicidad y complejidad, mostrando que no siempre se necesitan reglas complicadas para obtener resultados ricos. Además de estos, se encuentran fractales en la naturaleza.
Triángulo de Sierpinski
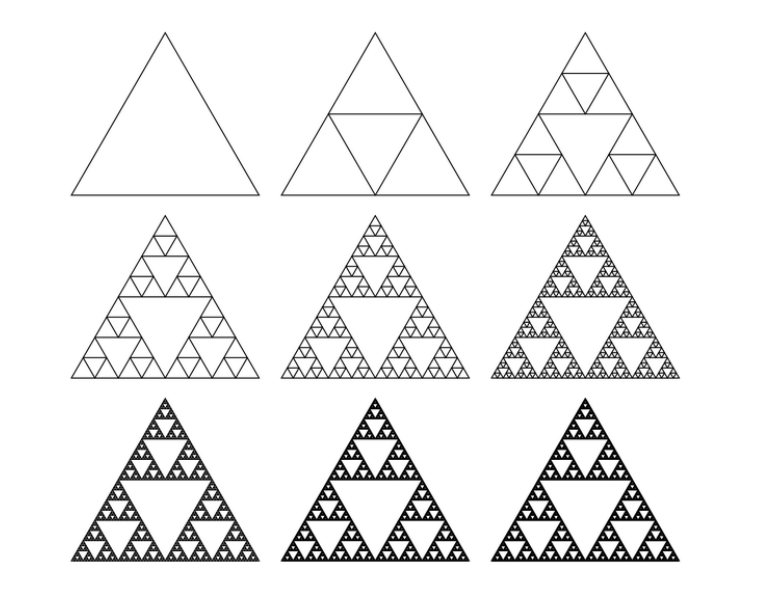
El triángulo de Sierpinski es otro de los fractales más famosos, ya que su construcción es geométrica y muy intuitiva, lo que lo convierte en una excelente herramienta pedagógica para introducir la geometría fractal.
El proceso comienza con un triángulo equilátero, luego se divide en cuatro triángulos más pequeños y se elimina el triángulo central. Este procedimiento se repite indefinidamente en cada uno de los triángulos restantes.
El resultado es una figura llena de huecos, donde cada parte es una copia reducida del todo, cumpliendo perfectamente con la idea de autosimilitud.
¿Por qué es tan importante el Triángulo de Sierpinski? 📐
- Es el ejemplo más claro de autosimilitud: Al observar cualquier sección del triángulo, se repite exactamente la misma estructura. Esta propiedad lo convierte en el ejemplo más intuitivo para explicar qué es un fractal, incluso a personas sin formación matemática avanzada.
- Desafía la geometría clásica: Tiene área que tiende a cero a medida que el proceso continúa; posee un perímetro infinito y su dimensión fractal no es entera (no es 1 ni 2). Esto demuestra que existen formas geométricas que no encajan en la geometría euclidiana tradicional, lo que fue clave para el desarrollo de la geometría fractal en el siglo XX.
Este fractal es frecuente en arte generativo y diseño gráfico por su estética minimalista.
Aunque parezca abstracto, el Triángulo de Sierpinski tiene aplicaciones prácticas, por ejemplo, en antenas fractales, ya que su forma permite captar múltiples frecuencias usando menos materia
Curva de Koch
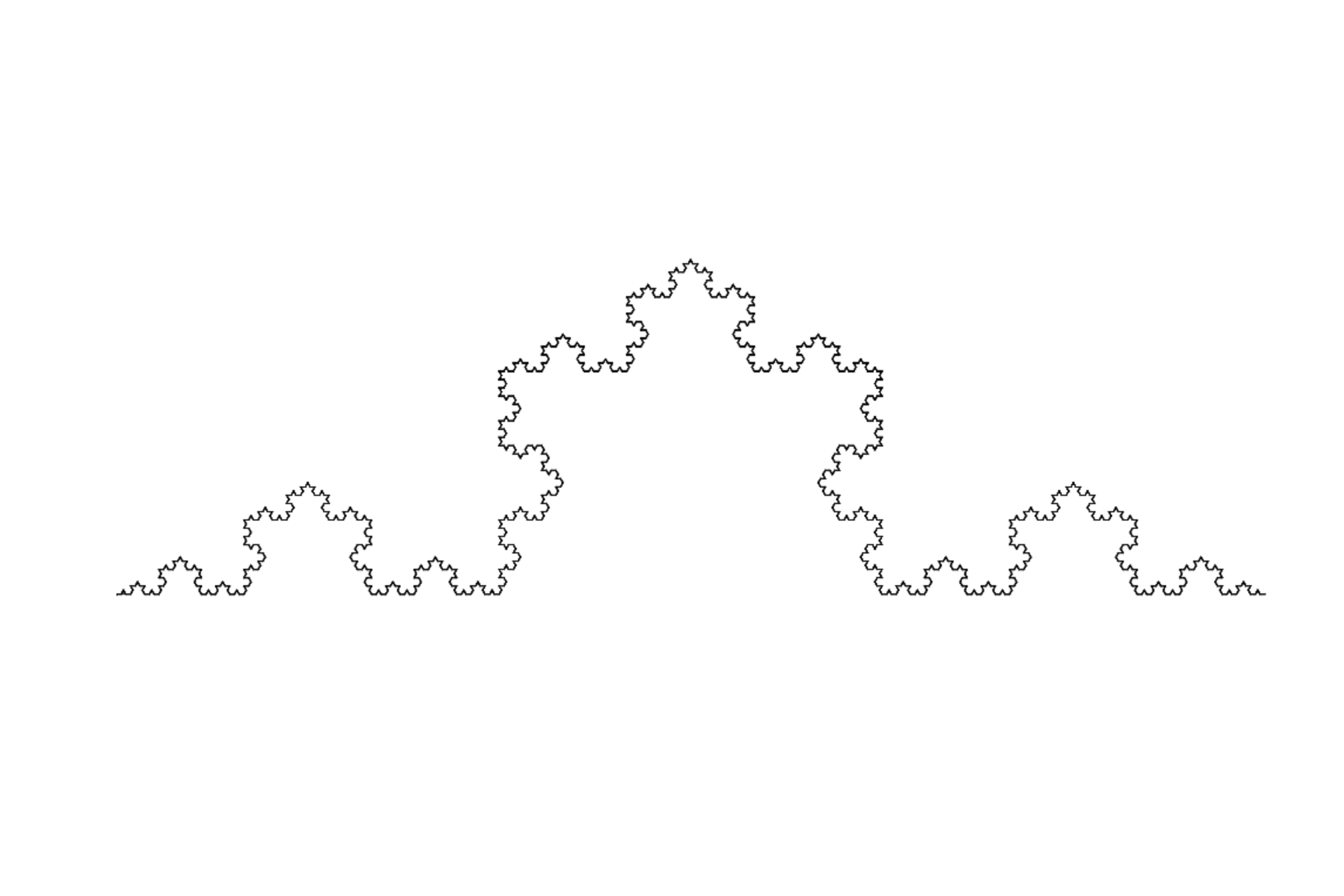
La Curva de Koch, también conocida como Copo de Nieve de Koch, es uno de los fractales famosos más antiguos. Su construcción comienza con un segmento de línea recta, que se transforma mediante un proceso iterativo.
Primero se divide el segmento en tres partes iguales, después se reemplaza el segmento central por dos segmentos que forman un pico triangular, luego este proceso se repite en cada nuevo segmento, indefinidamente. Cuando se aplica esta regla a los tres lados de un triángulo equilátero, se obtiene el famoso copo de nieve.
¿Por qué es tan importante la Curva de Koch? 📐
- Fue uno de los primeros fractales de la historia: La Curva de Koch fue introducida en 1904 por un matemático sueco, mucho antes de que existiera el término “fractal”.
- Ayuda a comprender la relación entre lo finito y lo infinito: El Copo de Nieve de Koch es una herramienta pedagógica clave para explicar procesos infinitos con resultados finitos y la diferencia entre crecimiento ilimitado y convergencia.
Es una figura precursora de la geometría fractal que demuestra que la matemática ya exploraba formas “irregulares” décadas antes de su formalización moderna.
Este fractal tiene una paradoja fascinante. Por un lado tiene un perímetro infinito, cada iteración aumenta la longitud total de la curva, y por otro un área finita, ya que a pesar del perímetro infinito, el área encerrada converge a un valor limitado.
Esponja de Menger
La Esponja de Menger lleva la idea de los fractales al espacio tridimensional: es una extensión natural del concepto del triángulo de Sierpinski, pero aplicada a un cubo.
El proceso de construcción es el siguiente: Se divide un cubo en 27 cubos más pequeños (como un cubo de Rubik 3×3×3); se eliminan el cubo central y los cubos centrales de cada cara; y el procedimiento se repite indefinidamente en los cubos restantes.
¿Por qué es tan importante la Esponja de Menger? 📐
- Es el fractal tridimensional más emblemático: A diferencia de otros fractales famosos (como el triángulo de Sierpinski o la Curva de Koch), la Esponja de Menger se desarrolla en tres dimensiones, lo que la convierte en un modelo esencial para estudiar fractales espaciales.
- Es la extensión natural del Triángulo de Sierpinski: Puede entenderse como la versión 3D del Triángulo de Sierpinski ya que ambos se construyen eliminando partes centrales, son totalmente autosimilares y tienen área/volumen decreciente y perímetro/superficie creciente.
Este fractal demuestra que los principios de la autosimilitud y la iteración no se limitan al plano, sino que también se aplican al espacio volumétrico.
Hasta el día de hoy, la Esponja de Menger se usa en aplicaciones concretas ya que su estructura es ideal para analizar cómo circula el aire, los fluidos o la energía en sistemas altamente perforados.
Información clave
- Los fractales son estructuras geométricas que exhiben patrones auto-similares a diferentes escalas, desafiando las nociones tradicionales de dimensión y forma.
- Los fractales más famosos incluyen el Conjunto de Mandelbrot, el Triángulo de Sierpinski, la Curva de Koch y la Esponja de Menger.
- El Conjunto de Mandelbrot es quizás el fractal más emblemático, definido por la iteración de la función compleja f(z) = z² + c.
- El triángulo de Sierpinski es otro de los fractales más famosos, ya que su construcción es geométrica y muy intuitiva.
- Los fractales también se usan en el trading
📚 Bibliografía
- Mandelbrot, B. B. (1977/1982). The fractal geometry of nature. W. H. Freeman and Company. Recuperado de https://archive.org/details/fractalgeometryo00beno
- Ponce-Campuzano, E. (2023). 5.5: The Mandelbrot Set en Complex Analysis: A Visual and Interactive Introduction. LibreTexts. Recuperado de https://math.libretexts.org/Bookshelves/Analysis/Complex_Analysis_-_A_Visual_and_Interactive_Introduction_(Ponce_Campuzano)/05%3A_Chapter_5/5.05%3A_The_Mandelbrot_Set
¿Te gustó este artículo? ¡Evalúalo!
Cargando...
