Aprender matemáticas suele ser una pesadilla para estudiantes de todos los cursos y, a veces, no conocer la base es precisamente el problema. Tanto si te apasionan las matemáticas como si quieres repasar algunos conceptos básicos; vamos a ver las bases sobre el número e en Matemáticas, que suele ser una noción un poco abstracta y, demasiado a menudo, difícil de comprender. ¡Empecemos por el principio!
🧮 ¿Qué es el número e?
El número e, también conocido como número Euler, es un número irracional, es decir, que no puede expresarse como el cociente exacto de dos números enteros, ya que su número de decimales es infinito.
Su valor aproximado es 2.71828, y es un número fundamental en matemáticas, especialmente porque es la base de los logaritmos naturales, también llamados neperianos. ¿Por qué? Pues bien, porque el número e permite saber para qué valor el logaritmo neperiano es igual a 1. O dicho de otro modo, el logaritmo neperiano de x (ln x) es la potencia a la que se debe elevar el número e para obtener x.
No te preocupes si tienes dificultades en matemáticas, ¡puedo asegurarte que las mías son mucho mayores!
Albert Einstein.
Y si, a pesar de las palabras de Einsteir sientes preocupación de cara a tu próximo examen, siempre puedes acudir a un profesor de matemáticas. ¡Es más habitual de lo que piensas!
Valor del número e
Pero entonces, ¿cuánto vale e si el número de decimales que contiene es infinito? Lo primero para entender su valor es tener en cuenta que se trata de un número irracional. ¿Qué quiere decir esto?
Que, a diferencia de los números racionales, no se puede expresar mediante una fracción, y que su escritura decimal puede ser infinita y no es periódica.
Número racional
- Se puede representar con una fracción de dos números enteros.
- El denominador es distinto de cero.
- Su desarrollo decimal es periódico.
Número irracional
- No se puede expresar con una fracción.
- Su representación decimal no es exacta.
- Su expresión no es periódica.
¡Vamos a verlo mejor con un ejemplo!
Número racional:
- En la fracción 2/7 = 0,285714285714285714...
- Los dígitos que hay después de la coma son una secuencia lógica y recurrente de decimales.
Número irracional:
- Seguramente el número irracional más común es el número Pi, cuyo valor es 3,14159265358979323846264338327950288419716939937510582..., y que ha sido objeto de investigación de eruditos desde la antigüedad.
- También forma parte de este grupo el número e; en su caso, tiene un valor de 2,71828182845904523536028747135266249775724709369995957...
Para llegar a esta conclusión, matemáticos de todas las épocas han estudiado este número. Vamos a conocer un poquito sobre su historia. 👇
La historia del número e
Hay tres nombres importantes en la historia de este número que se expresa con la letra e: John Napier, que desarrolló los logaritmos; Jacob Bernoulli, que descubrió el número e gracias al interés compuesto de las inversiones; y Leonhard Euler, que descubrió su irracionalidad. Y en cierto modo todo esto fue una cuestión de dinero... 💰 Vamos paso a paso, que este tema tiene "tela".
John Napier y los logaritmos
El número e hizo su aparición en el siglo XVII con el desarrollo de los logaritmos, gracias al trabajo de investigación del matemático escocés John Napier (1550-1617). En su libro de referencia, que data de 1614, Napier presenta una herramienta para simplificar los cálculos matemáticos: el logaritmo.
En el siglo XVII, no existían las calculadoras ni los ordenadores, pero eso no significa que no hubiera investigaciones matemáticas. Ya en el siglo III a.C. Arquímedes se había dado cuenta de que bastaba con sumar los números para multiplicar ciertos números gracias a las potencias (el exponente).
Lo que hizo Napier fue ampliar el trabajo de Arquímedes desarrollando un método para hacer sumas en lugar de multiplicaciones; restas en lugar de divisiones; y divisiones por 2 en lugar de extracciones de raíces cuadradas. Así nacieron las primeras tablas de logaritmos decimales con 8 decimales.
- Mejor con un ejemplo:
.
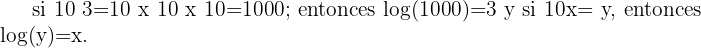0️⃣Te interesa: si también quieres conocer la historia y propiedades del número 0, te sorprenderá lo relacionadas que pueden estar las "mates" con la religión y la cultura de las antiguas civilizaciones...
Jacques Bernoulli y el interés compuesto
A finales del siglo XVII, el número e se definió como la base del logaritmo neperiano. El matemático Jacques Bernoulli (1654-1705) se interesó por encontrar el valor máximo de los intereses de los préstamos utilizando la técnica de interés compuesto. Esta consistía en añadir, con la mayor frecuencia posible, el interés acumulado a la cantidad original depositada para maximizar la ganancia.
💸 Te lo explicamos con dinero:
Con 1 € prestado a una tasa de interés del 100 %, si el interés del capital se calcula anualmente, la deuda es de 2 € al final del año. Pero, si calculamos mensualmente, obtenemos 2,61 € al final del año, y 2,71 € si el interés se calcula diariamente.
Bernoulli se dio cuenta de que el interés compuesto se estanca a medida que uno aumenta la frecuencia de cálculo del interés. Así, calculado cada segundo, el interés es el mismo que el diario (2,71 €). Con esta demostración, J. Bernoulli descubrió el número e.
Leonhard Euler y la notación moderna
Sin embargo, fue el matemático suizo Leonhard Euler (1707-1783) quien, un poco más tarde, se interesó por el número e, tomando su nombre de la letra inicial de la palabra "exponencial".
Euler demostró en 1737 la irracionalidad del número e sobre la base del desarrollo continuo de fracciones, y determinó el desarrollo de e en serie mediante la factorización, sabiendo que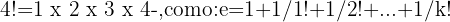 
.
- Conclusión: cuanto más aumentas el valor de k, más se acerca el valor obtenido a e.
🔠 La letra e no es la única que representa un número... Descúbrelo todo sobre el número i.
Propiedades matemáticas del número e
El primer uso del número e, si bien no había sido realmente teorizado, fue el de la búsqueda de la ganancia máxima al aumentar la frecuencia de cálculo de las tasas de interés de un préstamo: el método de interés compuesto en progresión continua que acabamos de ver, de J. Bernoulli.
Desde la obra de L. Euler, el número de decimales conocidos ha aumentado constantemente de forma exponencial. Aumentó de 18 decimales conocidos en 1748 a 2010 decimales en 1949, luego a 116 000 en 1978, a 10 millones en 1994, a 1,25 mil millones en 1999, hasta alcanzar los 5 mil millones de decimales en 2016.
¿Por qué? ¿Gracias a qué? Evidentemente, es el poder de la informática lo que permite estos récords, que un cerebro humano no puede igualar.
Pero llegado este punto, seguramente te preguntarás, ¿para qué sirve el número e, cuáles son sus propiedades matemáticas? ¡Vamos a verlas!
1️⃣ Para el análisis complejo, en la que es clave para resolver funciones exponenciales complejas. Se utiliza para establecer la relación entre funciones trigonométricas y funciones exponenciales complejas.
2️⃣ Para determinar cuál es la relación, en geometría, entre las caras y los vértices de los poliedros.
❗Antes de seguir: ¿Sabes cuáles son los números primos? Difícilmente podrás continuar con el número e si no tienes buena base...
Fórmulas y aplicaciones que usan el número e
Como hemos visto más arriba, la fórmula de Euler es, posiblemente, una de las más estudiadas que se sirve del número e. Esta fórmula fue descubierta por el científico suizo con la ayuda del matemático francés Abraham De Moivre. Y es la siguiente: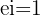 
Como ves, esta no solo integra el número Pi, uno de los números más famosos de las Matemáticas, y el número e, sino también el número imaginario i. Estos tres números forman parte de los números más conocidos e importantes.
Además de esta, Leonhard Euler, descubrió otra fórmula que, esta vez, no dependía únicamente del álgebra. De hecho, la fórmula conecta el álgebra del número e con la trigonometría. Así, encontró: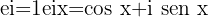 
. Una fórmula que podrá detallarte tu profesor de matemáticas.
Fórmulas importantes
Además de esta fórmula, hay otras que también son muy importantes, por los usos que tienen:
1️⃣ La fórmula del interés compuesto continuo: esta fórmula tiene varios usos relacionados con las finanzas. Cuando veas cada elemento que la compone, lo entenderás un poco mejor. ¡Seguro!
La fórmula: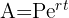 
.
- Aquí A es la cantidad calcular.
- P es el capital, la cantidad de dinero que se invierte en un principio.
- r es la tasa de interés anual.
- t los años
- y el número e, del que llevamos hablando ya un buen rato.😉
2️⃣ La fórmula de la distribución normal (campana de Gauss): esta fórmula se utiliza mucho en estadística.
La fórmula: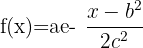 
- Donde a = altura del pico de la curva
- b = posición del centro del pico
- c = desviación típica
- f(x) = función de x
- e = número de Euler
- x = entero
👨🏫 ¿Dudas con estas fórmulas? Va subiendo el nivel, ¿verdad? Aprovecha la facilidad de poder preguntarlas en cualquier momento a tu profesor de matemáticas online.
Campos de uso del número e
Muchas veces se tiene la sensación, cuando se está estudiando para los exámenes, de que muchos ejercicios de Matemáticas son inútiles o al menos no se utilizarán en la vida cotidiana: conocer la raíz cuadrada de cada número, las ecuaciones diferenciales, la factorización y la derivación, la función exponencial, el logaritmo, los números perfectos, etc.
Pero, si indagamos un poco, nos damos cuenta de que sí que se utilizan estos conceptos, aunque no lo sepamos o nos demos cuenta. De hecho, usamos el número e siempre que queremos estimar una magnitud exponencial:
- En el cálculo y análisis matemático: derivadas e integrales.
- En Economía y finanzas: crecimiento exponencial en tasas de interés.
- En Física: modelado de fenómenos naturales como el decaimiento radiactivo.
- En Biología: estudios de poblaciones y tasas de crecimiento.
El número e en la vida cotidiana
Ya hemos visto algunos campos en los que se usa el número e, uno de los más especiales, junto al número áureo, de las "mates"; pero ¿y en el día a día? ¿Sabrías poner un ejemplo de cuándo se usa el número e? La periodista Noelia Freire da, para National Geographic 2, algunos muy ilustrativos y sencillos de comprender.
- Ejemplo 1: seguro que has dicho o escuchado la expresión "está creciendo exponencialmente", como los precios, por ejemplo. 😅 Exacto, este tipo e incrementos están definidos por el número e.
- Ejemplo 2: algo más complejo, pero también habitual; cuando vamos al banco o valoramos una inversión del tipo que sea, el número e está presente en la fórmula que nos dirá cómo podría crecer esa inversión en el futuro.
- Ejemplo 3: en biología nos ayuda a entender cómo un grupo crece o disminuyen en el tiempo.
Como hemos visto, el número e forma parte del álgebra en matemáticas, así como del aprendizaje de los y las estudiantes de prácticamente todos los niveles, aunque no lo sepan; y es que es la base de la fórmula exponencial, es decir, de las funciones.
También comprenderás cómo funcionan las fracciones y cómo usarlas conociendo este número; así como la diferencia entre los números racionales e irracionales.
Por tanto, es importante comprender esta parte del álgebra y, por ese motivo, si no te ha quedado claro, siempre es recomendable profundizar más y resolver dudas con un profesor particular de matemáticas si es necesario. Ya que una forma de estudiar y comprender el número e y sus fórmulas son las clases particulares que te darán la oportunidad de repasar lo que no hayas entendido en clase.
¡Y si lo has entendido todo, también puedes ir a por nota! El profesor o profesora te acompañará y se tomará su tiempo para explicarte todas las complejidades del número e y su uso; deteniéndose justo donde te perdiste en clase y adaptando los ejercicios a tu nivel para que progreses de forma eficaz.
Bibliografía
- Crecimiento exponencial. (s/f). Gob.pa. Recuperado el 22 de enero de 2025, de https://www.inec.gob.pa/redpan/sid/glosario/WebHelp/Crecimiento_exponencial.htm
- Freire, N. (2024, enero 18). El número e: una de las constantes fundamentales dentro de las matemáticas. National Geographic. https://www.nationalgeographic.com.es/ciencia/numero-e-euler-a-vida-cotidiana_21407
¿Te gustó este artículo? ¡Evalúalo!
Cargando...
Muy informativo e ilustrativo
¡Gracias, Christian!
Me gustó mucho. Muchas gracias
¡Nos pone muy contentos saberlo! :D Gracias
Bueno pues sigamos con el fascinante mundo de las matemáticas
la verdad es que me ayudó mucho
¡Gracias por hacérnoslo saber!
¿Por qué es tan importante un número tan desangelado y aparentemente humilde, del montón, como 2,7182…? ¿Y no uno más redondo como 1, 2, 5, 10…?
He leído que a causa de que la derivada de e^x es igual a dicha potencia [(e^x)’=e^x] y eso facilita mucho la derivación de ecuaciones con potencias de base numérica (frente a, verbigracia, 2^x, 3^x,…).
¿Hay algún/os otro/s motivo/s?
¡Excelente pregunta! 😊 El número e es fundamental porque tiene propiedades matemáticas únicas, como la que mencionas: la derivada de e^x es e^x, lo que facilita mucho los cálculos en matemáticas, especialmente en problemas de crecimiento exponencial, finanzas y física. Además, e aparece naturalmente en muchos procesos del mundo real, como en la modelización de fenómenos de crecimiento, decaimiento, y en la teoría de probabilidades. 🌱✨ Su importancia va mucho más allá de ser solo una base para derivadas. ¡Es realmente fascinante!