Un número perfecto es aquel igual a la suma de sus divisores propios positivos, excluyéndose a sí mismo. Los primeros estudios que se tienen de los números perfectos son los de Euclides, alrededor del 300 a.C.
Las matemáticas han existido desde el principio de los tiempos. Si creemos en el descubrimiento del hueso de Ishango (hace más de 20 000 años), esta puede que sea la primera prueba del conocimiento de los primeros números primos y la multiplicación. Descubre todo sobre los números perfectos en este artículo.

Origen y significado de los números perfectos
Los números perfectos están relacionados con la búsqueda de los números primos de Mersenne. La proposición 36 del libro IX de Elementos de Euclides dice que si el número de Mersenne 2n - 1 es primo, entonces 2n-1 (2n - 1) es un número perfecto.

René Descartes confirmó en una carta a Mersenne que cualquier número perfecto par es euclidiano, pero no demostró su teoría.
En cambio, el matemático suizo Leonhard Euler fue el primero en dar una demostración a la observación de Descartes. La combinación de los resultados de Euclides y Euler permitió obtener una caracterización completa de los números perfectos pares.
Los primeros cuatro números perfectos se conocen desde la antigüedad. Se encuentran en las obras de Nicómaco de Gerasa y Teón de Esmirna. El quinto número perfecto se menciona en un códice latino de 1456. Los números perfectos sexto y séptimo fueron encontrados por Cataldi en el siglo XVI y el octavo en 1772 por Euler.1
Así, a principios de la década de los 50, conocíamos 12 números perfectos, pero después la búsqueda se aceleró a través de técnicas cada vez más sofisticadas y el uso de ordenadores en la década de los 90 gracias al GIMPS (Great Internet Mersenne Prime Search).
¿Quieres saber más sobre el número e?
- Importancia en la teoría de números y matemáticas modernas
Si los números primos son reconocidos como la base misma de la aritmética por muchos matemáticos, los números perfectos no tienen una utilidad particular, en el sentido de que no se utilizan para resolver una ecuación, una factorización y no entran en el campo de la criptografía.
Antiguamente, eran considerados superiores a todos los demás y algunos vieron un papel místico en ellos: «El seis es un número perfecto en sí mismo, no porque Dios creó todas las cosas en seis días, sino que Dios creó todas las cosas en seis días porque ese número es perfecto» - San Agustín en La ciudad de Dios (420 d.C.)
Son uno de los misterios de las matemáticas, y la búsqueda de nuevos números perfectos sigue fascinando a muchos matemáticos en la actualidad.

Las conjeturas en relación con los números perfectos son numerosas. Una conjetura es una regla que nunca ha sido probada. Aquí tienes tres:
- Los números perfectos de Euclides son todos pares, ya que uno de los factores es una potencia de 2. Pero nada prueba, por el momento, que no haya números perfectos impares;
- Todos los números perfectos conocidos terminan en 6 o 28, pero de nuevo eso puede no ser siempre así;
- Tampoco se ha demostrado que realmente haya infinitos números perfectos.
¿Te interesa conocer también el número 0?
Características de los números perfectos
Lo que es un número perfecto está claro y es muy sencillo. Lo difícil es encontrarlos. Verás a continuación:
Propiedades de los números perfectos
- Es un número entero positivo
- Es un número igual a la suma de sus divisores propios positivos
Para entenderlo, mira cuáles son los primeros ocho números perfectos y por qué:
- 6: Sus divisores propios (1, 2, 3) suman 6.
- 28: Sus divisores propios (1, 2, 4, 7, 14) suman 28.
- 496: Sus divisores propios (1, 2, 4, 8, 16, 31, 62, 124, 248) suman 496.
- 8 128: Sus divisores propios suman 8 128.
- 33 550,336: Sus divisores propios suman 33 550,336.
- 8 589 869 056: Sus divisores propios suman 8 589 869 056.
- 137 438 691 328: Sus divisores propios suman 137 438 691 328.
- 2 305 843 008 139 952 128: Sus divisores propios suman 2 305 843 008 139 952 128.
Echa un ojo también a nuestro artículo sobre el número i.
Relación de los números perfectos con los números primos
Un número primo de Mersenne es un número primo que cumple:
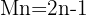
Ten en cuenta que cuando relacionamos números perfectos con números primos, nos estamos refiriendo exclusivamente a los números primos de Mersenne. ¿Por qué? Porque Euclides desarrolló una fórmula con la cual todos los números eran perfectos cuando el paréntesis era un número primo de Mersenne.
Por lo cual, a medida que se descubren números primos de Mersenne, puede haber la posibilidad de que se descubra también un número perfecto.
El último y más elevado número primo de Mersenne descubierto es el 

¿Conoces el número áureo?
Teorema de Fermat

El teorema de Fermat (1640) es:
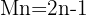
si Mn es primo, entonces n es primo.
Para establecer que cuando 2 n - 1 es primo, n es primo, hay que demostrar la afirmación si n es compuesto, entonces 2 n - 1 también es compuesto.
Es decir, n = ab, con a, b > 1, y la identidad xk - 1 = (x - 1) (x k-1 + x k-2 + · · · + x + 1) en la que
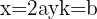
Entonces 2ab - 1 = (2a - 1) (2a (b-1) + 2a (b-2) + · · · +2a + 1), que muestra que
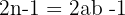
es compuesto, ya que factoriza como dos factores, cada uno mayor que 1 (porque a > 1).
Teorema de Euclides
El teorema de Euclides: si Mn es primo, entonces 2n-1 Mn es un numero perfecto.
Admitimos la función σ(n) como la suma de todos los divisores del entero positivo n. Un número perfecto k se caracteriza por σ(k) = 2k.
La función σ tiene la siguiente propiedad: si a y b son dos naturales primos entre ellos, entonces
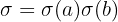
Descubre nuestra oferta de clases particulares de matematicas en Superprof.
Vamos a recapitular algunas de las curiosidades sobre los números perfectos que mencionábamos en otros apartados del artículo, a ver si así te entra el gusanillo de investigar más sobre estos números especiales:
Todos los números perfectos hallados son pares y terminan en 6 u 8. ¿Por qué? ¿No puede haber números perfectos impares? Parece que impar no es sinónimo de perfecto... Esto sigue siendo un misterio. Actualmente no se han encontrado números perfectos impares pero tampoco hay un argumento que demuestre que no existen; por lo tanto la posibilidad sigue existiendo.2
Decirte que hoy en día conocemos un total de 48 números perfectos. No es un número muy elevado, ¡y mira por cuales cifras nos movemos ya! Se cree que existen infinitos números primos de Mersenne de los que obtendríamos infinitos números perfectos (¡pares!). Pero, el quid de la cuestión es que aún no se ha conseguido aclarar si existen infinitos números perfectos o no.
Lista de números perfectos
Aunque todos los matemáticos están de acuerdo en que existe una infinidad de ellos (nunca se ha demostrado), hoy en día solo conocemos 50, sin siquiera estar seguros de que no haya números intermedios perfectos sin descubrir desde el 47.
El último número perfecto se descubrió en enero de 2018. El descubrimiento de un nuevo número primo muy grande implica el descubrimiento de un nuevo número perfecto y eso es lo que sucedió con el número 2⁷⁷²³²⁹¹⁷-1.
Hay solo tres números perfectos inferiores a 1000: 6, 28 y 496. Aparentemente, los números perfectos pares terminan en 6 u 8, aunque esto nunca se ha demostrado, pero no de forma alternativa sistemáticamente.
Los números perfectos pares de la fórmula 2n-1 (2n - 1) son números triangulares (e incluso hexagonales). Por otro lado, todos los números perfectos pares, excepto el primero, son la suma de 2(n-1)/2 primeros cubos impares. Por ejemplo:
- 28 = 13+ 33,
- 496 = 13+ 33 + 53 + 73,
- 8128 = 13+ 33 + 53 + 73 + 93 + 113 + 133 + 153.
Por cierto, ¿ya lo sabes todo sobre el número Pi?
Te habrás dado cuenta de que no hay números perfectos impares. Todos los ejemplos son números pares, pero eso no significa que no haya un número perfecto impar.
Aunque las investigaciones avanzan, ninguna ha podido afirmar o refutar esta hipótesis. Carl Pomerance ha publicado un método heurístico que sugiere la inexistencia de un número perfecto impar.
Números perfectos del 1 al 100

En este rango, solo hay un número perfecto: el ✨ 6 ✨.
¿Cómo saber que el 6 es un número es perfecto?
El 6 es un número perfecto porque sus divisores propios positivos son 1, 2 y 3. Si los sumamos (1 + 2 + 3), obtenemos como resultado 🥁... 6.
Un divisor propio positivo de un número es un factor positivo de ese número que no sea el propio número. Así, los divisores propios de 6 son 1, 2 y 3 (pero no 6).

Números triperfectos, multiperfectos e hiperperfectos
Sobre la base de los números perfectos, también hay números triperfectos, multiperfectos e hiperperfectos.
Tranquilo, seguro que tu profesor matematicas no te pregunta sobre ellos, pero si quieres saber más, aquí tienes algo de información.

Los números triperfectos
Un número triperfecto es siempre par. Si hay un impar, es mayor que 1050. La suma de los divisores de un número triperfecto, incluido él mismo, es igual a tres veces el número. Por ejemplo, 120 es un número triperfecto porque 23 * 3 * 5 = 120.
Solo conocemos estos triperfectos:
- 120
- 672
- 776
- 818 240
- 476 304 896
Aclara todos estos conceptos con un profesor online matematicas.
Los números multiperfectos
La suma de los divisores de un número multiperfecto, incluido él mismo, corresponde a k veces el número.
Los matemáticos han descubierto más de 500 números multiperfectos hasta el orden 8 y creen que conocen todos los multiperfectos de orden 3 a 7:
- 25x 33 x 5 x 7 es el primer tetraperfecto,
- 27x 34 x 5 x 7 x 11 x 17 x 19, el primer pentaperfecto,
- El más grande conocido es 7,3 101345
Los números hiperperfectos
Un número hiperperfecto es tal que
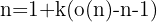

Un número 1-hiperperfecto es un número perfecto.
Un número 2- hiperperfecto (HP) tiene la fórmula
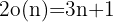
21, 2 133, 19 521, 176 661...
Un número 3-HP tiene la fórmula 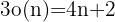 :
:
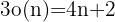
325 y ningún otro hasta n = 1 000 000
4-HP: 1 950 625, 1 222 640 625, 186 264 514 898 681 640 625
No hay ningún 5-HP conocido
6- HP: 301, 16 513, 60 110 701, 1 977 225 901, 2 733 834545 701, 232 630 479 398 401.
Saber los números perfectos, triperfectos, multiperfectos e hiperperfectos no te ayudará a hacer los ejercicios de tus clases de matemáticas en secundaria, así que mejor céntrate en las fracciones, la división euclidiana, los logaritmos o el razonamiento en geometría.
Pero si continúas con las matemáticas, quién sabe, tal vez los números perfectos se conviertan en un tema de investigación por tu parte...
Descubre también la historia de los números primos.
Importancia de los números perfectos hoy
Para los estudiantes de matemáticas, conocer los fundamentos de los números perfectos es algo obligatorio; además de que suele ser un tema que despierta fascinación a los alumnos. Por lo que los números perfectos son un área activa de investigación dentro de la teoría de números.3
Aunque más allá del saber por saber, los números perfectos se han revelado útiles. Por ejemplo, en la simetría y estructuras algebraicas, ya que han servido para investigar simetrías y estructuras algebraicas en matemáticas más avanzadas, de lo que se ha beneficiado la física teórica y la teoría de cuerdas.
También hay conceptos derivados de los números perfectos, como los algoritmos para encontrar divisores, que pueden aplicarse a la criptografía.

Todo el misterio e incertidumbre que existe alrededor de estos números, lleva a los matemáticos a dedicar muchas horas de pensamiento a ellos. De hecho, hay problemas matemáticos abiertos que cualquiera puede poner a investigar y darle vueltas. Si necesitas apoyo para profundizar, puedes buscar clases particulares matemáticas en Logroño.
🫵 Te lanzamos el reto 🫵
¿Existen infinitos números perfectos?
Tanta perfección al final termina abrumando. Y en efecto, el mundo de las matemáticas es precioso y abrumador a la vez. Es increíble todo lo que se ha descubierto, pero más increíble aún es saber que esto es una mijilla en comparación con todo lo que queda por descubrir.
Ciencia, tecnología y ser humano en la búsqueda (¿infinita?) de nuevos enigmas y descubrimientos.
Esperamos que este artículo te haya resultado útil y haya despertado tu interés por este campo. ¿Serás tú quien siga sumando descubrimientos a la lista de números perfectos?
Descubre con Superprof los números más famosos de las Matemáticas.
Bibliografía
- Porras Ferreira, J. W. (mayo de 2024). «Los números perfectos». Research Gate. Fecha de última consulta: 14 de febrero de 2025. Disponible en: https://www.researchgate.net/publication/380513406_Los_numeros_perfectos
- «Número perfecto». Averroes Blog - Junta de Andalucía. Fecha de última consulta: 14 de febrero de 2025. Disponible en: https://blogsaverroes.juntadeandalucia.es/recursosdematematicas/numero-perfecto/
- Bueso Montero, J. L. (5 de febrero de 2024). «Números perfectos y matemáticos imperfectos». Universidad de Granada. Fecha de última consulta: 14 de febrero de 2025. Disponible en: chrome-extension://efaidnbmnnnibpcajpcglclefindmkaj/https://wpd.ugr.es/~academia/discursos/4%20Jose%20Luis%20Bueso%20Montero.pdf
Resumir con IA:
















No sé quien transcribió esto pero se equivocó con el primer número perfecto que sería 6 y no 8
¡Hola! Muchas gracias por tu comentarios. ¡Efectivamente tenías razón! Ya hemos modificado el artículo ;)
Pregunta ; ¿Cual es la utilidad de los números perfectos? ¿Se los utiliza para algo que explique algo del Universo? 0 para diseñar o construir algo hermoso o algo práctico para el ser humano?
550.336 NO es un numero perfecto, estoy estudiando programacion y como tarea me mandaron hacer un programa que calculase si un numero era perfecto o no, y me tire 1 hora mirando donde estaba el fallo porque me decia que 550.336 no es perfecto 50 minutos repitiendo los pasos en el programa uno a uno, me decidi por sacar los divisores yo mismo a papel y boli desubriendo que 550.336 no es un numero perfecto gracias por esta errata que me hizo darme cuenta que mi programa era perfecto no como el numero que aqui se afirma que si lo es cuando no
Lamentamos la confusión, y gracias por señalarlo. Tienes razón, 550.336 no es un número perfecto. Un número perfecto es aquel cuya suma de sus divisores propios positivos (excluyendo el propio número) es igual al número en sí mismo. Un ejemplo de número perfecto es 28, ya que sus divisores propios (1, 2, 4, 7, 14) suman 28.
Es genial que hayas descubierto la discrepancia y que tu programa de programación esté funcionando correctamente. Si tienes alguna pregunta o necesitas ayuda con tu tarea de programación en el futuro, no dudes en preguntar. Estamos aquí para ayudarte :)