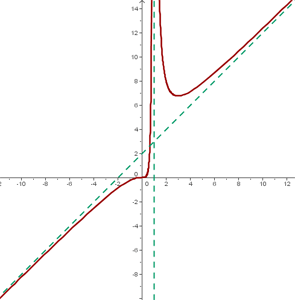
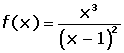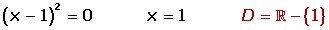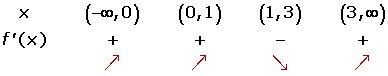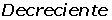Función estrictamente creciente
f es estrictamente creciente en a si sólo si existe un entorno de a, tal que para toda x que pertenezca la entorno de a se cumple:

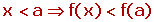

La tasa de variación es positiva.
Función creciente
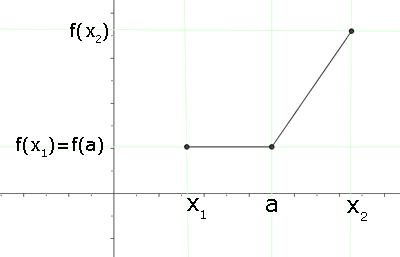
f es creciente en a si sólo si existe un entorno de a, tal que para toda x que pertenezca la entorno de a se cumple:

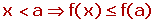
La tasa de variación es positiva o igual a cero.
Función creciente en un punto
Si f es derivable en a:
f es estrictamente creciente en a si:
f'(a) > 0
Intervalos de crecimiento
Para hallar el crecimiento y decrecimiento seguiremos los siguientes pasos:
1.
Derivar la función.
2.
Obtener las raíces de la derivada primera, para ello hacemos: f'(x) = 0.
3.
Formamos intervalos abiertos con los ceros (raíces) de la derivada primera y los puntos de discontinuidad (si los hubiese)4.
Tomamos un valor de cada intervalo, y hallamos el signo que tiene en la derivada primera.
Si f'(x) > 0 es creciente.
Si f'(x) < 0 es decreciente.
5.
Escribimos los intervalos de crecimiento y decrecimiento.Ejemplo
Calcular los intervalos de crecimiento y decrecimiento de la función: