El teorema del valor medio o de Lagrange dice que:
Sea f es una función continua en [a, b] y derivable en (a, b), existe un punto c 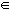


La interpretación geométrica del teorema del valor medio nos dice que hay un punto en el que la tangente es paralela a la secante.
El teorema de Rolle es un caso particular del teorema del valor medio, en el que f(a) = f(b).
Ejemplos
1.
¿Se puede aplicar el teorema de Lagrange a f(x) = 4x2 − 5x + 1 en [0, 2]?f(x) es continua en [0, 2] y derivable en (−1, 2) por tanto se puede aplicar el teorema del valor medio:


2.
¿Se puede aplicar el teorema de Lagrange a f(x) = 1/ x2 en [0, 2]?La función no es continua en [−1, 2] ya que no definida en x = 0.
3.
En el segmento de la parábola comprendido entre los puntos A = (1, 1) y B = (3, 0) hallar un punto cuya tangente sea paralela la cuerda.Los puntos A = (1, 1) y B = (3, 0) pertenecen a la parábola de ecuación y = x2 + bx + c.

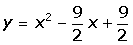
Por ser la función polinómica se puede aplicar el teorema del valor medio en el intervalo [1, 3].
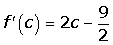

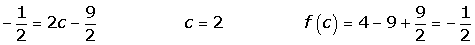
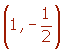
4.
Calcular un punto del intervalo [1, 3] en el que la tangente a la curva y = x3 − x2 + 2 sea paralela a la recta determinada por los puntos A(1, 2) y B(3, 20). ¿Qué teorema garantiza la existencia de dicho punto?Hallamos la ecuación de la recta que pasa por los dos puntos.
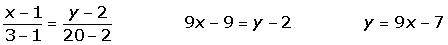
Por ser y = x3 − x2 + 2 continua en [1, 3] y derivable en (1, 3) se puede aplicar el teorema del valor medio:
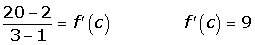


5.
Determinar a y b para que la función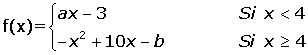
cumpla las hipótesis del teorema de Lagrange en el intervalo [2, 6].
En primer lugar se debe cumplir que la función sea continua en [2, 6].
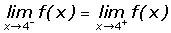

En segundo lugar se debe cumplir que la función sea derivable en (2, 6).



