Si una función es derivable en un punto x = a, entonces es continua para x = a.
El reciproco es falso, es decir, hay funciones que son continuas en un punto y que, sin embargo, no son derivables.
Ejemplos
Estudiar la continuidad y derivabilidad de las funciones:
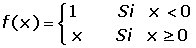
En primer lugar estudiamos la continuidad en x = 0.
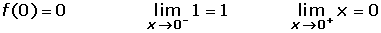
La función no es continua, por tanto tampoco es derivable.


En primer lugar estudiamos la continuidad en x = 0.
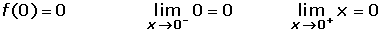
La función es continua, por tanto podemos estudiar la derivabilidad.

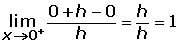
Como no coinciden las derivadas laterales no es derivable en x = 1.
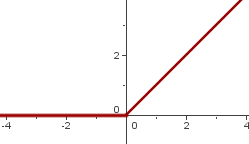
f(x) = x2 en x = 0.
La función es continua en x= 0, por tanto podemos estudiar la derivabilidad.
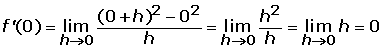
En x = 0 la función es continua y derivable.

Dada la función:

¿Para qué valores de a es derivable?

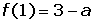
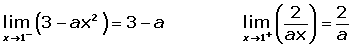


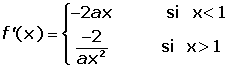


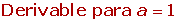

Estudiar para qué valores de a y b la función es continua y derivable:
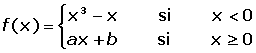
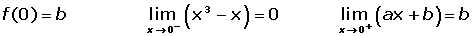

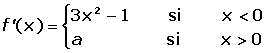


Determinar los valores de a y b para quien la siguiente función sea derivable en todos sus puntos:
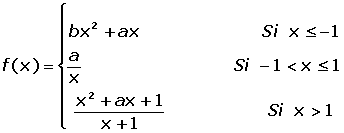
Para qué una función derivable tiene que ser continua En este caso la función no es continua para x = 0 cualesquiera que sean a y b, es decir, no existen valores de a y b que hagan continua la función.
Por tanto, no existen a y b para los cuales la función sea derivable.
Estudiar para qué valores de a y b la función es continua y derivable:
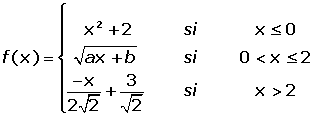
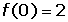


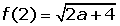



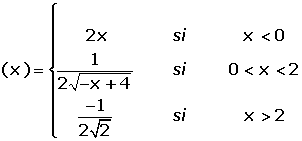




Estudiar la continuidad y derivabilidad de la función definida por:
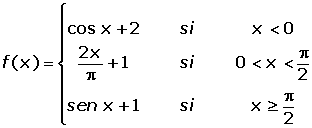
La función no es continua en x = 0 porque no tiene imagen. Por tanto tampoco es derivable.


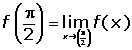
Por lo que es continua, veamos si es derivable mediante las fórmulas de derivadas trigonómetricas inmediatas.
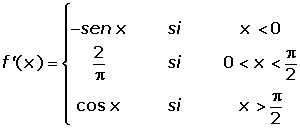
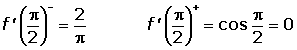
Como las derivadas laterales no coinciden no es derivable en el punto.

