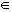Qué significa propiedad de darboux en Matemáticas

Si una función es continua en el intervalo [a, b] y k es un número comprendido entre los valores f(a) y f(b), entonces existe algún c en (a, b) tal que f(c) = k

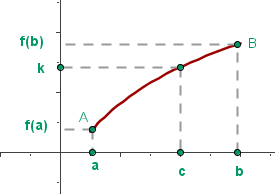
Si Observamos el dibujo podemos definir la propiedad de Darboux de este otro modo:

Si una función es continua en el intervalo [a, b] la función alcanza en este intervalo todos los valores comprendidos entre f(a) y f(b).

Probar que la función f(x) = x(sen x +1) toma el valor 2.

La función es continua en toda 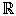por se el producto de dos funciones continuas.

Tomamos el intervalo y estudiamos el valor de las imágenes de los extremos:

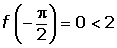
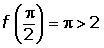
Por tanto existe un c tal que f(c) = 2