El producto escalar de dos vectores es un número real que resulta al multiplicar el producto de sus módulos por el coseno del ángulo que forman.

Ejemplo
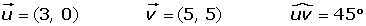

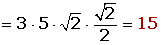
Expresión analítica del producto escalar

Ejemplo

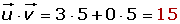
Expresión analítica del módulo de un vector
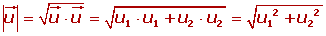

Ejemplo
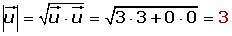
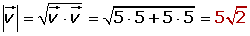
Expresión analítica del ángulo de dos vectores
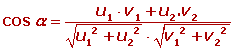
Ejemplo

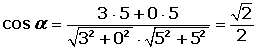
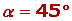
Condición analítica de la ortogonalidad de dos vectores

Ejemplo



Interpretación geométrica del producto escalar
El producto de dos vectores no nulos es igual al módulo de uno de ellos por la proyección del otro sobre él.
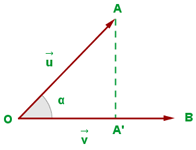

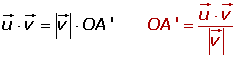
OA' es la proyección escalar de 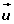
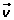
El vector proyección se calcula multiplicando la proyección escalar por un vector unitario de 
La proyección escalar del vector u sobre v es el módulo de la proyección vectorial de u sobre v.
Ejemplo
Hallar la proyección del vector 
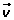

Propiedades del producto escalar
1
Conmutativa
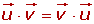
2
Asociativa

3
Distributiva

4
El producto escalar de un vector no nulo por sí mismo siempre es positivo.
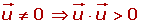
Producto escalar de vectores del espacio
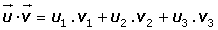
Ejemplo
Hallar el producto punto de dos vectores cuyas coordenadas en una base ortonormal son: (1, 1/2, 3) y (4, −4, 1).
(1, 1/2, 3) · (4, −4, 1) = 1 · 4 + (1/2) · (−4) + 3 · 1 = 4 −2 + 3 = 5
Expresión analítica del módulo de un vector
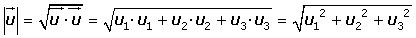
Hallar el valor del módulo de un vector de coordenadas 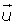
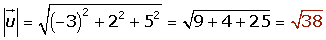
Expresión analítica del ángulo de dos vectores

Determinar el ángulo que forman los vectores