Una teoría matemática se considerará perfecta solo si se ha hecho de una forma tan clara que la pueda entender el primer individuo que pase por la calle.
David Hilbert, matemático alemán
Las matemáticas son una rama del conocimiento muy extensa. En la enseñanza y las clases particulares de matemáticas es una materia que tenemos siempre y, junto con lengua, es de las materias que más horas 🕖 semanales tiene. Esto se debe a que la lectoescritura y el pensamiento analítico se revelan como los pilares para poder vivir en sociedad con un nivel de educación mínimo.
Entre los contenidos que tenemos que aprender en nuestra trayectoria académica en la asignatura de matemáticas, está el aprender qué es una función afín: una función afín es una función polinómica de primer grado cuya expresión general es y = mx + n, donde m representa la pendiente y n la ordenada en el origen.
Esta es una unidad que se suele ver por primera vez en 2.º de la ESO y se consolida en 3.º y 4.º. Si ya has empezado con este tema, pero no terminas de comprenderlo o necesitas un poco de repaso y práctica, hemos preparado este artículo dedicado a las funciones afines.

Definición y características de la función afín
Expresión general y componentes
Una función afín es una función matemática que se representa mediante una línea recta en un gráfico 📈. Se expresa con la fórmula f(x) = mx + b, donde «m» y «b» son números reales. En esta fórmula, «m» es la pendiente de la recta, que indica su inclinación o la tasa de cambio, y «b» es el valor donde la recta cruza el eje vertical (eje y).
Una función afín es aquella cuya fórmula sigue el patrón y=mx+n, donde m y n son números distintos de cero.
Por ejemplo, las funciones 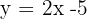 y
y 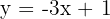 son ejemplos de funciones afines. Estas funciones representan gráficamente una línea recta, pero no necesariamente pasan por el origen de coordenadas.
son ejemplos de funciones afines. Estas funciones representan gráficamente una línea recta, pero no necesariamente pasan por el origen de coordenadas.
En términos más generales, una función afín asocia, para cualquier valor x definido en ℝ (la escala de los números reales), el número ax + b, donde a y b son números reales. Este tipo de funciones tienen una forma lineal y se caracterizan por tener una pendiente (representada por m) y un término independiente (representado por n) que determinan la posición 📍 y la inclinación de la línea en el plano cartesiano.
Representamos esta función mediante la ecuación siguiente: 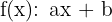
El número «b» debe ser diferente a 0. ¿Por qué? Porque si b = 0, entonces tenemos que 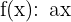 y entonces hablamos de una función afin lineal.
y entonces hablamos de una función afin lineal.
Si «a» es igual a cero, entonces decimos que la función 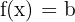 es constante (y afín); de hecho, todos los puntos de la misma línea tienen el mismo eje de ordenadas (b) y la curva será paralela al eje de abscisas. Estas son las dos particularidades que tendrás que tener en cuenta 👀 con la función afín.
es constante (y afín); de hecho, todos los puntos de la misma línea tienen el mismo eje de ordenadas (b) y la curva será paralela al eje de abscisas. Estas son las dos particularidades que tendrás que tener en cuenta 👀 con la función afín.
El valor «b» representa, en una representación gráfica, la ordenada en el origen: es el punto donde la curva pasa por el eje de ordenadas (y) en su distancia desde el origen (0).
La variable «a», denominada «coeficiente de dirección», hace referencia al grado de la pendiente de la curva, calculable a partir del eje de abscisas (x) en la gráfica.
Cuanto mayor sea el número «a», mayor será la pendiente de la curva, que podrá ser positiva o negativa.
Para causar una buena impresión 💫 en los ejercicios de representación gráfica matemática en la prueba de acceso a la Universidad, podrás escribir que la recta de f(x) mide la tasa de aumento de las ordenadas por unidad de abscisas.
Por lo tanto, una función afín es un conjunto de valores que resuelve la ecuación 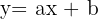 , en el intervalo dado, y cuya representación gráfica tomará la forma de una recta oblicua, creciente o decreciente.
, en el intervalo dado, y cuya representación gráfica tomará la forma de una recta oblicua, creciente o decreciente.
Entonces, debemos leer que «f» es la función que en el número «x» coincide con el número «ax + b»: «x» es el antecedente, «ax + b», la imagen de «x» en el intervalo. El resultado escrito es f(x) = ax + b.
Por ejemplo, si 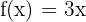 , obtendremos una recta, denominada d1, creciente, que corta el eje de ordenadas en el punto 0. Si
, obtendremos una recta, denominada d1, creciente, que corta el eje de ordenadas en el punto 0. Si  f(x) = -x, entonces tendremos la recta d2, que será decreciente.
f(x) = -x, entonces tendremos la recta d2, que será decreciente.
Otra peculiaridad que deberás tener en cuenta es que si 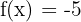 , entonces la línea será constante y cruzará el eje en el punto -5.
, entonces la línea será constante y cruzará el eje en el punto -5.
Para calcular la imagen de un «x» real, bastará con multiplicar «x» por el coeficiente «a» y sumar la constante «b». Entonces, podremos comenzar a dibujar ✏️ la recta en la gráfica.
¡Descubre en qué consiste la división euclídea!
Diferencias entre función afín y función lineal
Entre tantas funciones es normal que nos hagamos un lío, aunque el nombre que tiene cada función nos da muchas pistas. Las funciones más estudiadas en los primeros niveles de la ESO son la función afín y la función lineal. Muy importante no confundirlas ante su aparente similitud.
¿Cómo diferenciarlas? Partiendo de la base de que la gráfica de la función es una recta: si dicha recta pasa ✔️ por el punto de origen de coordenadas, es una función lineal  y su pendiente (m) es la ordenada de x = 1. Si esta recta NO ❌ pasa por el origen de coordenadas, es una función afin
y su pendiente (m) es la ordenada de x = 1. Si esta recta NO ❌ pasa por el origen de coordenadas, es una función afin  , en la que n es ordenada de x = 0 y m es la ordenada de x = 1 menos n.
, en la que n es ordenada de x = 0 y m es la ordenada de x = 1 menos n.
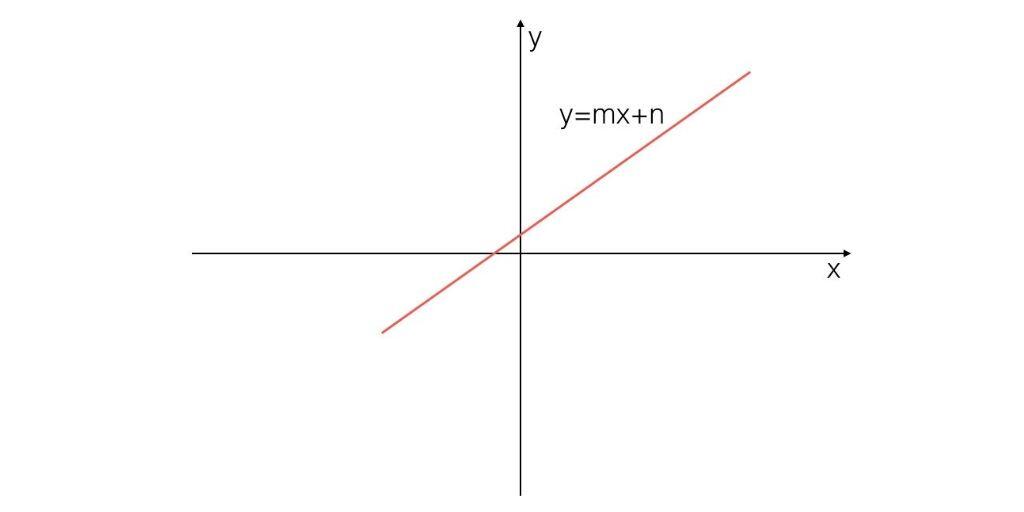
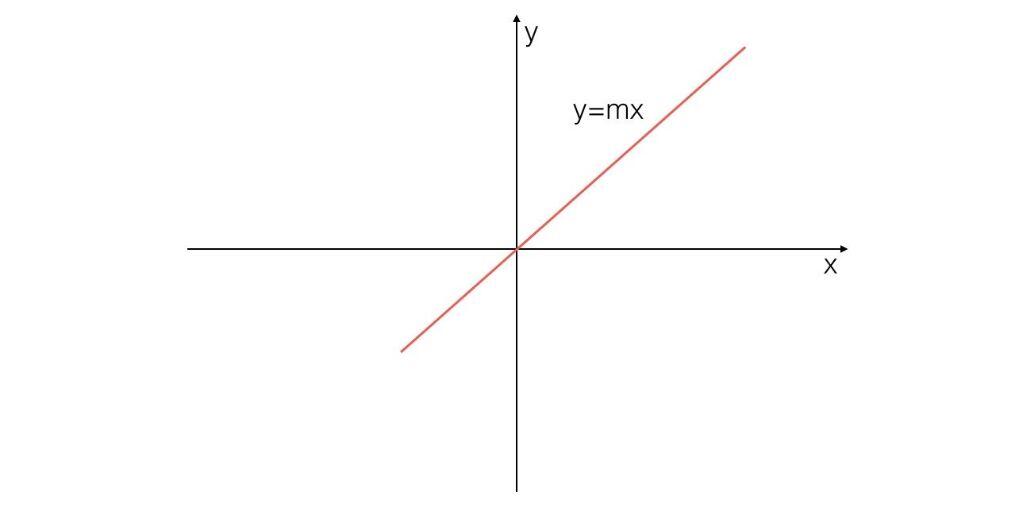
Representación gráfica de una función afín
Cómo graficar una función afín paso a paso
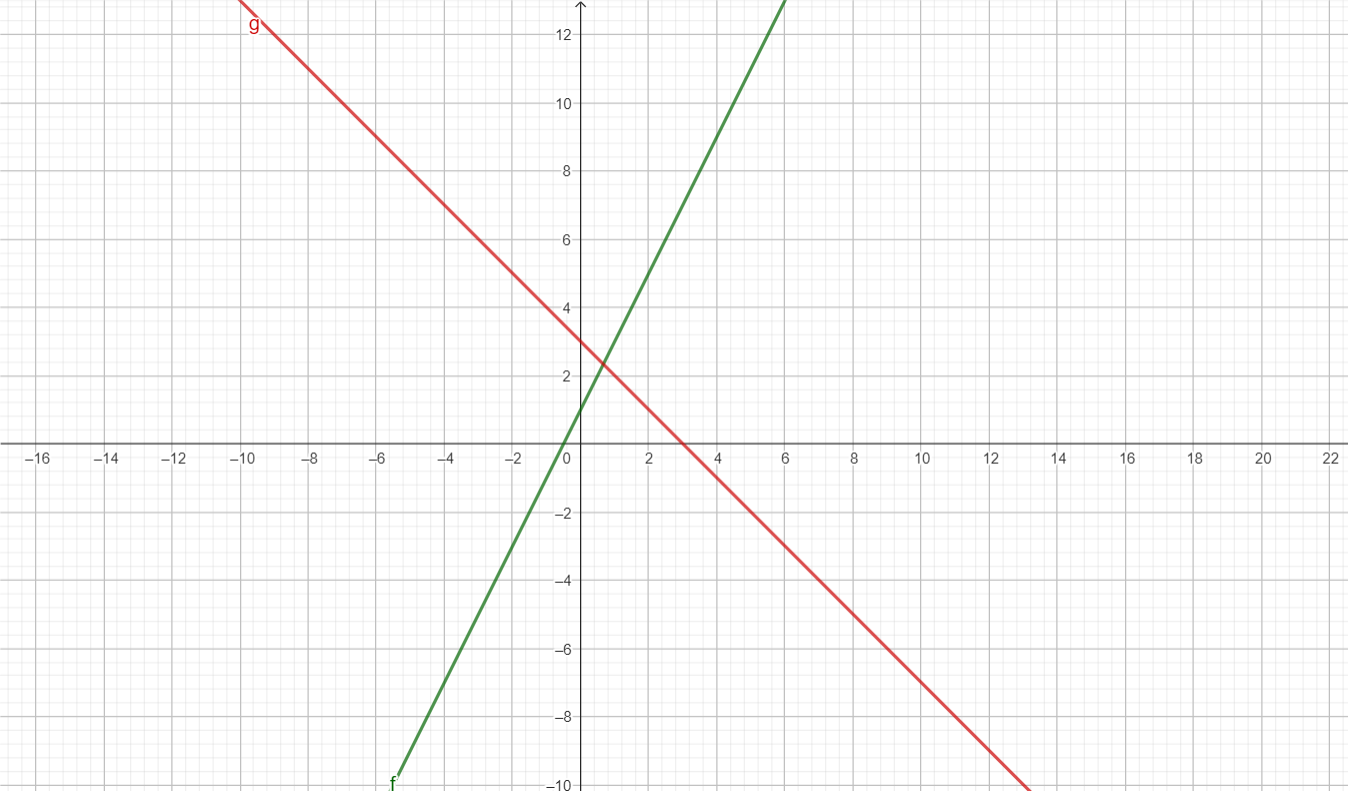
Aquí vemos representas las siguientes ecuaciones:
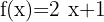 ;
; 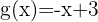
Si vives en la capital, no dudes en buscar clases particulares matematicas Madrid.
Existen diversos métodos para representar una función afín:
Método 1
Para poder representar la recta de una función afín, tomemos como ejemplo la siguiente función:
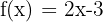
La función f(x) tiene la forma 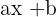 , siendo a = 2 y b = -3, por lo que se trata de una función afín.
, siendo a = 2 y b = -3, por lo que se trata de una función afín.
Lo primero que tendremos que hacer para trazar la recta de la ecuación 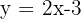 es hallar 🔎 dos puntos, que los buscaremos al azar a partir del cálculo de x:
es hallar 🔎 dos puntos, que los buscaremos al azar a partir del cálculo de x:
Para 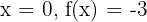 [PUNTO A]
[PUNTO A]
Para 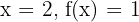 [PUNTO B]
[PUNTO B]
De este modo, obtenemos los puntos A y B cuyas coordenadas X e Y son para A = 0; -3 y para B = 2; 1.
Sin embargo, podemos agregar un tercer punto para evitar posibles errores y verificar que la hemos trazado bien. Por ejemplo, si le damos a «x» el valor de -2, obtendremos que 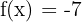 . De este modo, podremos trazar la recta de la ecuación
. De este modo, podremos trazar la recta de la ecuación 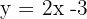 conectando los puntos entre sí.
conectando los puntos entre sí.
Si necesitas también teoría y problemas sobre qué es el álgebra, consulta este otro artículo.
Método 2
Comienza por la ordenada -3, «sube» 4 unidades en el eje y desplaza 2 unidades hacia la derecha en el eje x, o «sube» 6 unidades en el eje de ordenadas y 3 en el de abscisas.
Cuando «x» aumenta en 1, «y» aumenta en dos, de ahí que obtengamos que a = 2.
De este modo, obtenemos las siguientes coordenadas: A (0, -3), B (2, 1) y C (3, 3), lo que nos permitirá dibujar la recta d1, donde cada punto de la línea cumple con la ecuación 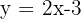 .
.
Para trazar la recta en el plano cartesiano, se deben seguir tres sencillos pasos:
- Representar los puntos calculados en el sistema de ejes 📌
- Unir mediante una línea recta utilizando una regla 📏
- Extender la recta hacia ambos lados y añadir flechas para indicar que continúa indefinidamente ↗️
Descubre aquí qué es la geometría.
Interpretación de la pendiente y la ordenada en el origen
Pendiente alta (m grande) → recta más inclinada
Pendiente baja (m pequeña) → Recta más suave
M positiva → inclinación hacia arriba
M negativa → inclinación hacia abajo
La pendiente influye no solo en la inclinación, sino también en la rapidez con la que cambia y respecto a x. Ahora bien, ¿cuál es el significado del punto de corte con el eje Y? 🤔 Se trata del valor donde x = 0 y sirve como referencia inicial para trazar la recta. Por ejemplo, si n =−3, la recta pasa por (0, -3).
Propiedades y aplicaciones de las funciones afines
Crecimiento y decrecimiento
La función afin presenta un comportamiento extremadamente predecible, por lo que podemos saber muy fácilmente si va a ser creciente, decreciente o constante. Será creciente si m > 0, pues los valores de y aumentan a medida que x se incrementa; será decreciente si m < 0, pues y disminuye cuando x se incrementa; por último, será constante si m = 0, pues el valor de y es igual para cualquier x.
Para no perderte con tantos conceptos, puedes apuntarte a clases de matematicas online y aprender cómodamente desde casa.
Aplicaciones en la vida real
Puede que te preguntes 💭 para qué sirven estas funciones en la vida real, más allá de tus clases de matemáticas. Pues bien, déjanos explicártelo a través de la siguiente tabla:
| Área | Modelo afín típico | Descripción | Ejemplos concretos |
|---|---|---|---|
| Economía 💰 | 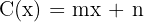 | El coste total se compone de un coste fijo (n) y un coste variable proporcional a la cantidad producida (m). | • Producción de bienes (coste fijo + coste por unidad). • Tarifas telefónicas: cuota fija + precio por minuto o GB. • Salarios con base + comisión por ventas. |
| Física 🧲 | 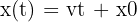 | Describe el movimiento rectilíneo uniforme: posición inicial más el desplazamiento generado por la velocidad constante. | • Automóvil a velocidad constante. • Movimiento de un ascensor entre plantas. • Cambio regular de temperatura en periodos cortos. |
| Ingeniería ⚙️ |  | Se usa para relacionar dos magnitudes que cambian de forma proporcional más un valor inicial. | • Relación lineal entre carga y deformación en ciertos materiales. • Consumo energético con gasto base + consumo por hora. • Conversión entre escalas (°C y °F). |
| Ciencias sociales / Estadística 📉 |  | Aproxima tendencias en datos observados: se analiza el cambio promedio entre variables. | • Predicción lineal de crecimiento poblacional en pequeños intervalos. • Encuestas con tasa base + variación proporcional. • Estimación de gasto mensual en función de un hábito. |
| Informática 🔌 |  | Aproximación lineal del tiempo de ejecución de algoritmos con complejidad 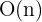 . . | • Procesos que aumentan su tiempo linealmente según el tamaño de entrada. • Coste computacional de recorrer listas o vectores. |
| Vida cotidiana 📔 | 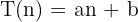 | Relación simple entre dos variables con un punto de partida y un cambio constante. | • Precio de taxis: bajada de bandera + coste por km. • Consumo eléctrico: cuota fija + coste por kWh. • Facturas del agua: mínimo mensual + coste por metro cúbico. |

Cómo determinar una función afín a partir de datos
Método analítico
Determinar una función f es fácil si conocemos los valores de «a» y «b». En nuestro ejemplo f(x) = 2x-3, decimos que  , que
, que 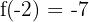 y que
y que 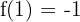 .
.
Así pues, el método analítico consiste en utilizar matemáticas puras 🔢 para determinar la función que pasa por dos puntos específicos. Como sabemos la expresión final de la función, pero queremos ver cómo se obtiene paso a paso, como si partiéramos de sus propiedades fundamentales, tenemos que seguir los pasos siguientes:
Identificar la pendiente (m)
En nuestro ejemplo (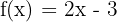 , el coeficiente que acompaña a x es 2, por lo tanto, la pendiente de la función es m = 2. Esto significa tres cosas:
, el coeficiente que acompaña a x es 2, por lo tanto, la pendiente de la función es m = 2. Esto significa tres cosas:
- Por cada unidad que aumenta x, el valor de la función aumenta en 2.
- La recta es creciente.
- Su inclinación es moderada, ni demasiado pronunciada ni demasiado suave.
Identificar la ordenadad en el origen (n)
También sabemos que, de nuestro ejemplo 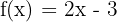 , el número sin x es -3, por lo que n = -3. ¿Qué significa esto? Que la recta corta el eje Y en el punto (0, -3) y que, cuando x = 0, el valor de la función es y = -3.
, el número sin x es -3, por lo que n = -3. ¿Qué significa esto? Que la recta corta el eje Y en el punto (0, -3) y que, cuando x = 0, el valor de la función es y = -3.
Construir la función afín
Sabiendo que la pendiente es m= 2 y la ordenada en el origen es n = -3, la función afín queda determinada por  . Esto da por finalizado ✅ el método analítico, con el que se ha podido identificar los parámetros y reconstruir la función a partir de ellos.
. Esto da por finalizado ✅ el método analítico, con el que se ha podido identificar los parámetros y reconstruir la función a partir de ellos.

Dado que las funciones se encuentran en el plan de estudios y en el currículo de los institutos, hace falta dominarlas.
No obstante, para analizar una función (estudiar los límites de las funciones, estudiar una función logarítmica o exponencial, hacer un cálculo integral, etc.), es fundamental comprender el lenguaje matemático 🔣.
Método gráfico
Es el método más sencillo pero, a partir de la segunda clase, la gráfica no siempre vendrá en los ejercicios.
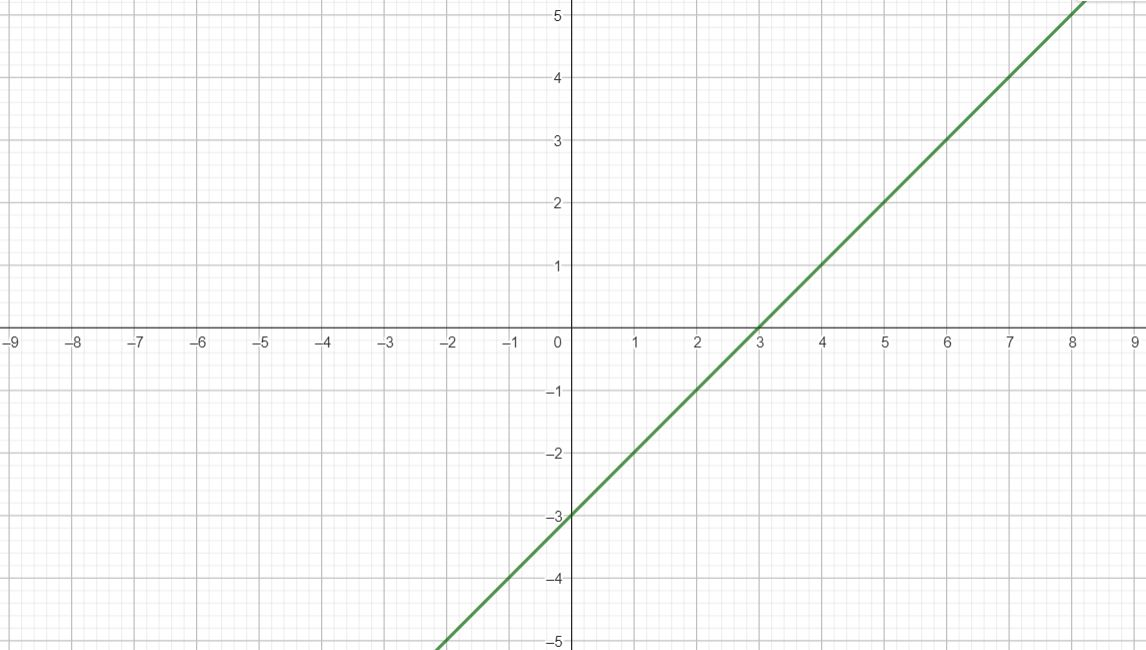
Para determinar gráficamente 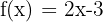 , bastará con ver qué puntos de la recta cortan los ejes X e Y. En nuestro caso, encontramos los puntos A (0; -3), B (2; 1) y C (3;3), de donde deducimos que la recta d1 presenta una ecuación de tipo
, bastará con ver qué puntos de la recta cortan los ejes X e Y. En nuestro caso, encontramos los puntos A (0; -3), B (2; 1) y C (3;3), de donde deducimos que la recta d1 presenta una ecuación de tipo 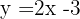 .
.
El símbolo «=» fue inventado en 1557 por el matemático Robert Recorde, quien dijo que lo eligió porque «no hay dos cosas más iguales que dos líneas paralelas».
¿Conoces nuestras clases particulares matematicas Barcelona?
Ejercicios sobre funciones afines
Ejercicio 1: Ejemplo de libro de secundaria
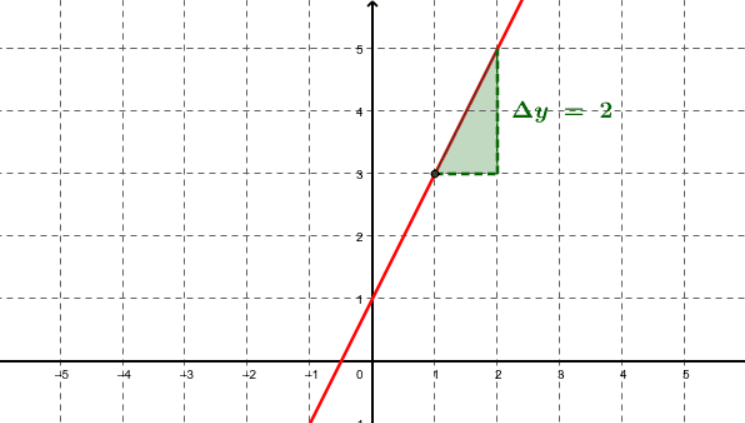
Tenemos estas cuatro fórmulas:
a) 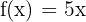
b) 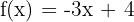
c) 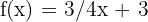
d) 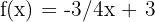
- ¿Cuál es la que define a la función?
- Dibuja sobre estos ejes la gráfica de
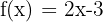
- Determina gráficamente el punto M de intersección de las dos rectas anteriores. Calcula las coordenadas exactas de M.
Ejercicio 2: Determinación de la ecuación a partir de dos puntos
Halla la ecuación de la función afín que pasa por los puntos (2, 5) y (6, 1).
Paso 1: calcular la pendiente (m)
La pendiente, como ya sabes, indica cómo cambia y respecto a x.
Tenemos que usar la fórmula:
Y sustituir:
Así, la interpretación visual que obtenemos es que la recta baja 4 unidades mientras avanza 4, por lo que se trata de una pendiente negativa.
¿Buscas un profesor particular matematicas Zaragoza?
Paso 2: calcular la ordenada en el origen (n)
Ahora utilizamos uno de los puntos, por ejemplo (2, 5):
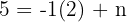
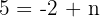
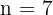
Esto significa que la recta cruza el eye Y en (0, 7).
Paso 3: escribir la función resultante
Ejercicio 3: Interpretación de la gráfica de una función afín

Dada una gráfica en la que la recta pasa por (0, 4) y (3, 1), determina:
La ecuación de la función afin
La pendiente
La ordenada en el origen
Paso 1: Identificar la ordenada en el origen (n)
La recta pasa claramente por el punto (0, 4), es decir,  . Esto se ve en la intersección con el eje Y.
. Esto se ve en la intersección con el eje Y.
Paso 2: Calcular la pendiente (m)
Usamos pues los dos puntos visibles:
Una vez hecho esto, la interpretación es la siguiente: la recta baja 3 unidades por cada 3 que avanza, es decir, la pendiente es -1. Además, su inclinación es descendente hacia la derecha. Por lo tanto, la ecuación final de la función es la siguiente:
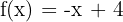
¿Buscas clases particulares matematicas Granada?
Tipos de funciones
Aunque no dudamos que con estos ejercicios seas ya un as de las funciones afines, es importante también que nunca las confundas con otros tipos de funciones. Si necesitas ampliar tus conocimientos, encontrarás un artículo del blog dedicado a cada tipo de función. Además, si necesitas más práctica, tenemos un montón de apuntes y ejercicios sobre funciones en nuestra página de material didáctico.
Veamos ahora otros tipos de funciones:
- Función acotada: función f tal que para cualquier valor de
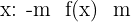
- Función algebraica: las que representan expresiones algebraicas de números y variables.
- Función compleja:
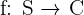 , donde C es el conjunto de los números complejos.
, donde C es el conjunto de los números complejos. - Función continua: función cuya curva está formada por un trazo continuo sin saltos.
- Función constante:
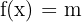 , donde m es constante.
, donde m es constante. - Función creciente: función f tal que f(x1) ≤ f(x2) para cualquier par de puntos x1 < x2
- Función cuadrática:
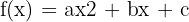
- Función cúbica:
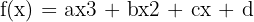
- Función decreciente: función f tal que f(x1) ≥ f(x2) para cualquier par de puntos x1 > x2.
- Función discontinua: función cuya curva está formada por un trazo con saltos o roto en su trazo.
- Función escalar:
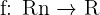
- Función explícita:
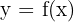
- Función exponencial:
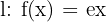
- Función identidad:

- Función impar:
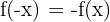
- Función implícita:
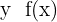
- Función inversa:
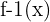
- Función lineal:

- Función logarítmica:
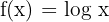
- Función par:
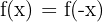
- Función parte entera:
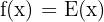
- Función periódica:
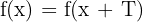
- Función polinómica:
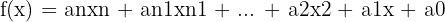
- Función potencial:
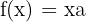
- Función primitiva:

- Función racional:
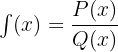 donde P y Q son dos polinomios.
donde P y Q son dos polinomios. - Función real:
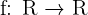
- Función trigonométrica: incluye en su fórmula alguna razón trigonométrica (seno, coseno, tangente...).
- Función valor absoluto:
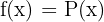 en la que P es un polinomio.
en la que P es un polinomio. - Función vectorial:
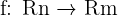
Descubre también nuestra definición de las tablas de multiplicar.
Ahora ya sabes lo que es una función afín y tienes problemas y ejemplos de funciones afines para que puedas practicar lo aprendido 🧠. Además, queremos presentarte otra opción para tus clases particulares de álgebra y matemáticas: Superprof. ¿Por qué no pruebas la primera gratis?
Resumen esencial de la función afin
- Una función afín tiene la forma f(x) = mx + n: m es la pendiente y n la ordenada en el origen.
- Se diferencia de la función lineal porque no siempre pasa por el origen (solo ocurre si n = 0).
- Para representarla se calculan dos o más puntos, se ubican en el plano y se unen con una recta.
- Su comportamiento depende de la pendiente: creciente (m > 0), decreciente (m < 0) o constante (m = 0).
- Se usa en múltiples contextos: costes fijos + variables, movimientos uniformes, consumos, predicciones lineales, entre otros.
- Para determinar su ecuación basta con hallar la pendiente a partir de dos puntos y luego calcular la ordenada en el origen.
📚 Bibliografía
- Larson, R., & Hostetler, R. (2018). Precalculus with Limits (7th ed.). Cengage Learning.
- Anton, H., Bivens, I., & Davis, S. (2013). Álgebra lineal con aplicaciones (9.ª ed.). John Wiley & Sons.
- Stewart, J. (2016). Cálculo de una variable (7.ª ed.). Cengage Learning.
Resumir con IA:

















gracias me ayudo muchicimo sigan asi
Qué bueno :) ¡Gracias por tu comentario!
Excelente explicación!
Me ayudó mucho. Saludos…
Whao es excelente! está explicación de verdad felicidades me encantó.
Nos alegra muchísimo saberlo. Gracias por tu comentario :)
:0 increible me encanto todo el contenido se me hizo de gran utilidad,muchas gracias
¡Genial! Nos da mucha felicidad saber que te ha sido útil. Gracias por tu comentario, Anastacia :)
exelente
Excelente muy bueno
Gracias, José :)
no entiendo , que se hache con el /, por ejemplo Y=1/2x -1
¿cómo se resolvería eso?
Entiendo que estás buscando una explicación sobre las funciones afines y cómo trabajar con una expresión como Y = (1/2)x – 1, específicamente con respecto al uso de la fracción (1/2). Vamos a abordar esto paso a paso:
Una función afín es un tipo de función lineal que se puede representar en la forma general:
Y = mx + b
Donde:
«Y» representa la variable dependiente.
«x» representa la variable independiente.
«m» es la pendiente de la línea.
«b» es la ordenada al origen, es decir, el valor de «Y» cuando «x» es igual a cero.
En tu ecuación Y = (1/2)x – 1:
«1/2» es la pendiente «m». Esto significa que por cada unidad que aumenta «x», «Y» aumenta en 1/2 unidad.
«-1» es la ordenada al origen «b». Esto indica que cuando «x» es igual a cero, «Y» es igual a -1.
Para resolver esta ecuación o representarla gráficamente, puedes seguir estos pasos:
Sustituye diferentes valores de «x» en la ecuación y calcula los valores correspondientes de «Y». Por ejemplo:
Cuando «x» es 0: Y = (1/2)(0) – 1 = -1
Cuando «x» es 2: Y = (1/2)(2) – 1 = 0
Cuando «x» es -2: Y = (1/2)(-2) – 1 = -2
Puedes usar estos puntos para trazar la línea en un gráfico cartesiano. Tendrás un punto en (0, -1), otro en (2, 0), y otro en (-2, -2). Conecta estos puntos con una línea recta.
La representación gráfica de esta ecuación será una línea recta que tiene una pendiente positiva de 1/2 y cruza el eje Y en el punto -1. La pendiente indica la inclinación de la línea, y el término independiente (-1) indica dónde corta el eje Y.
Esperamos que esto aclare cómo trabajar con la función afín Y = (1/2)x – 1 :) Si tienes más preguntas o necesitas más ayuda, no dudes en preguntar.
muchas gracias
Esta página me ayudo mucho tiene información importante
Gracias por tus comentario. Nos encanta saberlo :)
Hola gracias por esta página la verdad me ayudó pero no entiendo nose me resulta dificil
MUY BUENO EL ME AYUDO BASTANTE. GRACIAS
Nos alegra mucho saberlo :)