A lo largo de la historia, numerosos matemáticos han realizado aportes fundamentales que han moldeado el mundo tal como lo conocemos. Desde los teoremas de Pitágoras y Euclides en la antigüedad, pasando por las innovaciones de Newton y Euler en la era moderna, hasta las contribuciones contemporáneas de figuras como Alan Turing y Terence Tao, cada uno ha dejado una huella indeleble en el campo de las matemáticas.
La importancia de las matemáticas en la historia es incuestionable: podemos medir el tiempo ⌛, construir civilizaciones 🏙️, desarrollar sistemas de navegación 🧭, crear sistemas informáticos 👨🏼💻 y entender las leyes fundamentales del universo 🌌. Campos como la ingeniería, la física, la informática, la economía y, más recientemente, la inteligencia artifical, han podido florecer gracias a estos descubrimientos.
Siglos VI a. C. – III a. C.)
🏺 Antigüedad
Tales de Mileto: razonamiento lógico y deductivo en geometría Pitágoras de Samos: teorema de Pitágoras Euclides de Alejandría: base del método matemático formal Hipatia de Alejandría: pionera en geometría y astronomía
Siglos V - XV
🏰 Edad Media
Leonardo de Pisa: sistema numérico arábigo y sucesión de Fibonacci Omar Jayam: álgebra, ecuaciones cúbicas, calendario persa
Siglos XVII - XVIII
🌍 Renacimiento y Edad Moderna
René Descartes: geometría analítica Isaac Newton: cálculo infinitesimal y bases de la física clásica Leonhard Euler: análisis, teoría de números y notación matemática Sophie Germain: contribución a la teoría de números y la elasticidad
Siglo XIX
📐 Consolidación de las matemáticas modernas
Carl Friedrich Gauss: teoría de números, estadística y geometría Bernhard Riemann: geometría diferencial e hipótesis de Riemann
Siglo XX
💡 Era de la computación y la abstracción
Emmy Noether: álgebra abstracta y teorema fundamental Alan Turing: bases de la computación moderna e inteligencia artificial Emmy Noether: figura clave del siglo en matemáticas y física
Siglo XXI
🚀 Matemáticas contemporáneas
Grigori Perelmán: conjetura de Poincaré Terence Tao: análisis armónico y teoría de números

Matemáticos de la Antigüedad
Ellos sentaron las bases del pensamiento lógico y del razonamiento matemático formal como lo conocemos hoy en día. Las ideas de Tales de Mileto, Pitágoras o Arquímedes son estudiadas y aplicadas en la actualidad, así que sin duda no hablamos de ningunos desconocidos.
Tales de Mileto
El gran filósofo griego de la antigüedad, Tales, es conocido por su famoso teorema (el teorema de Tales), que todos acabamos aprendiendo en el instituto. Pero, ¿sabemos realmente quién es? 🤔
Tales nació en Mileto (antigua ciudad griego, actualmente en Turquía) alrededor del año -625 a.C y es considerado uno de los siete sabios de la antigua Grecia. El joven matemático aprendió ciencia en Egipto gracias al conocimiento de los sacerdotes egipcios y babilónicos.

Posteriormente, aprendió geometría, astronomía y filosofía; las pirámides egipcias fueron, a menudo, objeto de experimentos científicos para el joven aprendiz. Tras unos años, Tales regresó a su hogar en Mileto para fundar la escuela 🏫 milesia. El gran matemático se convirtió en maestro y enseñó todos sus descubrimientos a sus discípulos mientras continuó su investigación en diferentes campos.
¿Buscas clases particulares matematicas Alicante? ¡Están en Superprof!
Para encontrar el teorema que conocemos hoy, se dice que Tales habría querido calcular la altura de una pirámide a través de la sombra de un palo. Así es como Tales inventó este famoso teorema:
Dibujemos un triángulo ABC y dos puntos D y E de las líneas (AB) y (AC) para que la línea (DE) sea paralela a la línea (BC), de tal forma que podamos decir que: AD / AB = AE / AC = DE / BC.
Tales también utilizó sus conocimientos en el campo de la astronomía y descubrió cómo usar la Osa Menor para guiar a los marineros en mar abierto, calcular la duración del año a través de los intervalos de los solsticios en los equinoccios, indicar la distancia recorrida por el sol ☀️ entre los dos trópicos, el repertorio de efemérides, etc.
Pitágoras de Samos
Justo antes del teorema de Tales, el plan de estudios de matemáticas contempla otro teorema bastante conocido: el teorema de Pitágoras. Los alumnos se conocen el teorema de Pitágoras al dedillo, pues es uno de los capítulos más importantes de la geometría. Pitágoras, cuyo nombre significa «anunciado por la Pythia», nació en la isla de Samos (Grecia) a finales del siglo VI a.C. La historia del científico es conocida solo por algunos escritos después de su muerte.
Pitágoras fue un estudiante talentoso y muy deportivo (participó en los Juegos Olímpicos de lucha 🤼♂️). Tenía intereses en filosofía, historia y ciencia y fue discípulo de Tales. Siguió los pasos de su maestro y se marchó para aprender las ciencias egipcias y babilónicas.
Cuando regresó a su isla con la idea de fundar una escuela, al igual que Tales, no fue bien recibido y se le prohibió la entrada en su ciudad natal.
Fue entonces cuando huyó a la Gran Grecia, donde finalmente creó su escuela, llamada escuela pitagórica. Junto a sus discípulos, el matemático empleó su tiempo en demostrar su teorema:
En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
Euclides de Alejandría
La vida y los descubrimientos de Euclides han cambiado muchas cosas en la enseñanza de las matemáticas. Trigonometría, razonamiento de álgebra, ecuaciones, fracciones, logaritmos, axioma de Euclides, la división euclidiana, la geometría euclidiana, el algoritmo de Euclides, etc.; hay numerosos temas de matemáticas que hoy en día constituyen la base de la investigación 🔍 del matemático.
Nacido en Atenas (Grecia) alrededor del año 330 a.C., Euclides fue profesor en la Escuela de Alejandría, frecuentó los pasillos de la gran biblioteca y el museo de la famosa ciudad. El matemático es conocido en todo el mundo por un trabajo escrito alrededor del año 300 a.C. llamado Elementos, considerado por muchos como «la Biblia de las matemáticas»; de hecho, el libro se ha vendido casi tanto como el libro sagrado ✝️.

Esta obra, dividida en 13 tomos, presenta teorías sobre la geometría plana y la aritmética (triángulos, líneas rectas paralelas, círculos, etc.). Euclides demostró el teorema de Pitágoras y explicó el funcionamiento del máximo común divisor y las divisiones euclidianas.
La división euclidiana no es más que la división tal y como se le explica al alumnado de primaria. Esto se hace con un dividendo, un divisor, un cociente y un resto. Euclides también explicó cómo encontrar el máximo común divisor (el divisor común más grande), es decir, encontrar el número común a dos números que permita dividirlos.
¿Vives en la capital? Descubre nuestras clases particulares matematicas Madrid.
Arquímedes de Siracusa
Arquímedes, gran matemático y físico de la Antigüedad, (287 a.C. - 212 a.C.) fue uno de los científicos más conocidos en el campo de la invención de máquinas. Después de estudiar astronomía con su padre, estudió en la prestigiosa escuela de Alejandría. Se codeó con grandes eruditos 👨🎓 y desarrolló teorías matemáticas que a menudo se demuestran en sus diversos trabajos.
Las matemáticas están en deuda con Arquímedes porque fue el primero en darle una explicación al número Pi.
Posteriormente, calculó la relación entre la circunferencia de un círculo y su diámetro y descubrió que el número resultante es siempre el mismo, independientemente del tamaño del círculo. Arquímedes también invirtió tiempo calculando áreas como el área bajo una parábola y otras figuras.
Arquímedes terminó su vida al servicio de la ciudad de Siracusa (Italia) para desarrollar máquinas de guerra (aspilleras, catapultas, etc.). Fue asesinado por un soldado romano durante el saqueo de Siracusa (212 a.C.), mientras estaba absorto dibujando figuras geométricas en la arena, y sus últimas palabras fueron «¡No perturbes mis círculos!».

Sus diversos cálculos matemáticos no se detienen allí, ya que el científico utiliza su conocimiento y sus experiencias para explicar lo que se llamará el «principio de Arquímedes». Este teorema permite explicar la fuerza que sufre un cuerpo sólido sumergido en un fluido (ya sea líquido 💧 o gas 💨). Arquímedes descubrió posteriormente el principio de la flotación, cuyo resultado es la construcción del barco más grande de la Antigüedad: el Siracusia.
¿Vives en la ciudad de la Alhambra? Descubre nuestras clases particulares de matematicas en Granada.
Matemáticos de la Edad Media
Muchas cosas sucedieron gracias al intercambio cultural entre Oriente y Occidente, y una de ellas fueron la transmisión y transformación de las matemáticas. Fibonacci y su sucesión numérica, así como la difusión del sistema numérico arábigo, o Jayam y su contribución en álgebra, son tan solo algunos ejemplos de esta época dorada de las matemáticas.
Omar Jayam
El matemático y astrónomo persa halló la solución a las ecuaciones de tercer grado y sus raíces a través de su expresión geométrica. Dedicó su vida al estudio de los números irracionales y desarrolló contenidos en álgebra.
Nacido en Nishapur (antigua ciudad de Jorasán, actual Irán) en 1048, Omar recibió una buena educación en ciencias y filosofía. Gracias a apoyos, consiguió elaborar su Tesis sobre demostraciones de álgebra y comparación, con la que logró gran prestigio. Además de matemático, fue un gran astrónomo 🪐, faceta a través de la cual hizo correcciones del antiguo calendario zoroástrico.
Por otro lado, también es un reconocido poeta de la literatura oriental, de la que se puede destacar su obra Rubaiyat.
Se dice 💬 que debemos a Jayam el hecho de que la incógnita de las ecuaciones se llame «x». Él denominó la incógnita shay, que significa «cosa», «algo» en árabe. El término se adoptó en castellano como «xay» y posteriormente se terminó utilizando únicamente la letra inicial de la palabra, la «x».
Si vives en la ciudad condal, seguro que te interesan nuestras clases particulares matematicas Barcelona.
Leonardo de Pisa
Uno de los matemáticas más influyentes de esta época y figura clave en la transmisión del conocimiento en matemáticas del que hablábamos antes, producto de la conexión entre Oriente y Occidente. Viajó por el Mediterráneo y entró en contacto con grandes matemáticos árabes, lo que le hizo comprender la superioridad del sistema numérico indo-arábigo frente a los números romanos ⚔️.
Fue así como, en su obra Liber Abaci (1202), introdujo dicho sistema en Europa, lo que facilitó enormemente el desarollo del comercio, la contabilidad y las matemáticas aplicadas.
En este libro aparece por primera vez la famosa sucesión de Fibonacci, una secuencia en la que cada número es la suma de los dos anteriores. Además de tener interés matemático, dicha sucesión se manifiesta también en patrones de la naturaleza 🏔️ (el crecimeiento de las plantas, las espirales de los caracoles, etc.).
Matemáticos del Renacimiento y la Edad Moderna
De camino hacia la modernidad, esta etapa marcó un punto de inflexión en la historia de las matemáticas con más de un avance decisivo. Descartes y su geometría analítica, Newton y el cálculo infinitesimal o Euler y sus muchas contribuciones a esta ciencia son los protagonistas del siguiente apartado.
Isaac Newton
Isaac Newton, nacido en Woolsthorpe, Lincolnshire, Inglaterra, no fue solo un matemático, sino que también destacó como físico, filósofo y astrónomo. Criado por su padre y su abuela materna, fue un alumno distraído en clase, pero muy talentoso para construir máquinas 📠 de todo tipo para divertirse.
Su familia decidió sacarlo de la escuela para que ayudara en la granja familiar; sin embargo, un maestro logró convencerla de que lo apuntasen en la Universidad de Cambridge, donde estudió aritmética, geometría, trigonometría, astronomía y óptica.
Cuenta la leyenda que Newton descubrió la gravedad al ver cómo las manzanas caían de un árbol.
¿Quieres ser el o la mejor de tus clases particulares de matemáticas? Hazlo con Superprof.
En el campo de las matemáticas, Newton introdujo el método de fluxiones así como el binomio de Newton, que demuestra que la fórmula «(a + b) n» se cumple siempre, independientemente del valor de n.
Utilizó sus experimentos con la luz 💡 para inventar el primer telescopio reflexivo, lo que constituiría todo un éxito en el mundo científico de la época. ¡Toda una gran vida como matemático!

René Descartes
Estudiar a René Descartes en matemáticas es un paso esencial para comprender la historia de las matemáticas y el funcionamiento de las ecuaciones. Descartes, nacido en Francia en 1596 en la aldea de La Haya, fue criado por su abuela materna en el seno de una familia burguesa, con un padre asesor del Parlamento de Bretaña.
René Descartes escribió muchas obras científicas durante su carrera; la primera fue El mundo, que describe muchos fenómenos físicos cotidianos, incluido el movimiento de la tierra alrededor del sol.
No obstante, su obra más famosa sigue siendo El discurso del método, publicada en 1637. Escrita enteramente en francés, en ella Descartes expone varias evoluciones matemáticas y usa letras para describir las incógnitas ❓ de una ecuación. Así es como empezamos a usar x, y, z o a, b, c. Descartes también expresa las potencias de una manera particular para el tiempo: en lugar de apuntar «xxxx», escribe «x4».
Pienso, luego existo.
René Descartes
También inventó la geometría analítica, que consiste en representar figuras mediante cálculos algebraicos a través de un sistema de coordenadas.

Leonhard Euler
Considerado una de las figuras clave de la ciencia de las matemáticas del siglo XVIII, Euler realizó aportes fundamentales en diversas áreas: el análisis matemático, la teoría de números, la geometría, la mecánica y la física matemática. Gran parte de la notación matemática que usamos hoy, por ejemplo, fue introducida por él:
Función exponencial
Letra para la unidad imaginaria
Funciones trigonométricas
Su famosa identidad de Euler (eiπ+1=0) se considera una de las expresiones más perfectas 💯 de las matemáticas, pues une conceptos fundamentales en una misma ecuación. Euler perdió gran parte de la vista en sus últimos años, pero eso no le impidió seguir trabajando de manera incansable.
Matemáticos del siglo XIX
El siglo XIX estuvo marcado por una consolidación del rigor de las matemáticas y, por otra parte, la aparición de nuevas ramas abstractas. Fue en ese entonces cuando las matemáticas dejaron de centrarse únicamente en la aplicación práctica y se empezaron a explorar estructuras más profundas.
Carl Friedrich Gauss
No todo el mundo tiene el honor de ser considerado el «príncipe 👑 de las matemáticas», pero es que Friedrich Gauss mostró un talento excepcional desde temprana edad. Hizo descubrimientos trascendentales en casi todas las ramas de la matemática y sus constribuciones abarcan la teoría de números, el álgebra, la estadística, la geometría y la astronomía.
Muchos de sus resultados fueron descubiertos rápidamente, pero no fue hasta años después que se publicaron gracias a otros matemáticos importantes. Esto, sin duda, demuestra que Gauss estaba adelantado a su tiempo 🕰️ en muchos aspectos y, además, le otorga el título de mejor matemático de la historia.
Bernhard Riemann
¿Te suena el concepto de geometría no euclidiana? A no ser que estudies matemáticas a cierto nivel, puede que no, pero lo cierto es que fue Riemann quien introdujo este concepto, que permite describir espacios curvos. Esto fue fundamental para que, décadas después, Einstein pudiese desarrollar la teoría de la relatividad 😮.
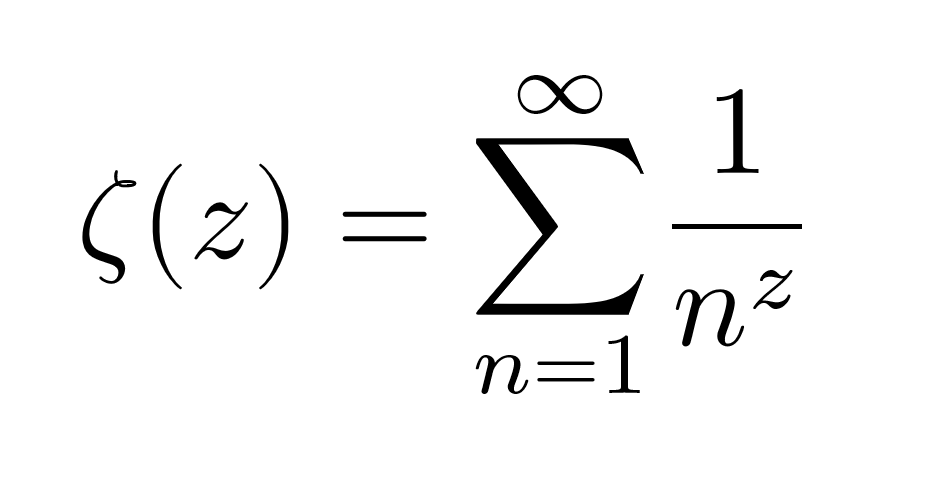
Sin embargo, su contribución más conocida es la hipótesis de Riemann, que se relaciona con la distribución de los números primos. El problema sigue sin resolverse y es considerado uno de los mayores desafíos de las matemáticas actuales.
Matemáticos del siglo XX y contemporáneos
El siglo XX y la actualidad representan una era de expansión sin precedentes, pues las matemáticas se enlazan ahora con computación, física y tecnología digital. Las teorías que surgen son abstractas, así que exploremos algunas de las ideas de los matemáticos más recientes.
Alan Turing
Damos un salto en la historia para plantarnos en el siglo XX y con él en la revolución tecnológica 📟. Todo lo aprendido y descubierto en matemáticas nos sirve ahora para aplicarla a prácticamente cualquier tecnología que desarrollemos. Una de las figuras que comenzó a germinar esta revolución fue Alan Turing gracias a sus investigaciones en la ciencia de la computación; de hecho, se le considera el precursor de la informática moderna.

Turing sentó las bases de la computación y sus teoremas, máquinas y pruebas siguen retando a grandes científicos a día de hoy. El matemático famoso sostenía que la máquina que había creado, la máquina de Turing, es capaz de resolver cualquier problema matemático que pueda representarse mediante un algoritmo. Para su corta vida, desarrolló investigaciones en varios campos, como la cibernética, la formación de patrones y la biología 🧬 matemática o el análisis criptográfico.
Grigori Perelmán
Te presentamos a una de las figuras más enigmáticas de las matemáticas contemporáneas, el matemático ruso Grigori Perelmán. En 2003 anunció la demostración de la conjetura de Poincaré, un problema que había permanecido sin resolver durante más de un siglo. Se convirtió así en el primer matemático 🎖️ en resolver uno de los Problemas del Milenio.
Sin embargo, Perelmán rechazó tanto la Medalla Fields como el premio económico asociado a la misma, bajo el argumento de que no le interesa lo más mínimo el reconocimiento público.
Terence Tao
Considerado uno de los matemáticos más importantes y brillantes de la actualidad, Terence Tao fue un niño prodigio y obtuvo su doctorado a temprana edad, centrándose en análisis armónico, ecuaciones diferenciales, combinatoria y teoría de números.
Además de destacar por su evidente amplitud de conocimientos, Tao es conocido por su capacidad para conectar 🧩 distintas áreas matemáticas. De esa forma, su trabajo ha permitido avances significativos en problemas bastante complejos como, por ejemplo, la distribución de los números primos.
Mujeres matemáticas que hicieron historia
A lo largo de la historia, son muchas las mujeres que han traído contribuciones decisivas a las matemáticas, a menudo enfrentándose a las ya conocidas barreras sociales y académicas. El trabajo de científicas como Sophie Germain, Emmy Noether o la mismísima Hipatia de Aljandría es hoy fuente de inspiración para las más jóvenes.
Sophie Germain
A esta matemática, física y filósofa le debemos el descubrimiento de un tipo de números que llevan su nombre: los números primos de Sophie Germain. Se trata de un conjunto de números primos cuyo doble incrementado en una unidad es también un número primo.
Su interés 🧐 por el mundo científico fue temprano y se centró especialmente en el estudio de la física. Fue autodidacta, ya que sus padres se opusieron en un primer momento a que desarrollara una carrera profesional en la ciencia. Finalmente consiguió tener acceso a la educación haciéndose pasar por un hombre, bajo el pseudónimo de Antoine Auguste LeBlanc.
El álgebra no es más que geometría en palabras, y la geometría es álgebra en dibujos.
Sophie Germain
Aunque trabajó en notables investigaciones científicas, no pudo vivir profesionalmente de ello y tuvo que depender económicamente de su familia toda la vida.
Emmy Noether
El teorema de Noether, resultado central en la física teórica que expresa que «cualquier simetría diferenciable que provenga de un sistema físico tiene su correspondiente ley de conservación», debe su nombre a esta matemática. Gracias a este enunciado se da una explicación a por qué existen leyes de conservación y magnitudes físicas que no cambian a lo largo de la evolución temporal de un sistema físico.
Las investigaciones de Emmy no solo se centraron en el campo de la física 👩🔬, sino que también revolucionaron las matemáticas con indagación sobre la teoría de los anillos (álgebra abstracta), la teoría de cuerpo (álgebra abstracta) o la de K-álgebras.

Posteriormente, tras acabar sus estudios y escribir la tesis, comenzó a impartir clases en la universidad en la que se había graduado, pero como sustituta de su padre. Después (1915), consiguió un puesto en la Universidad de Gotinga, en la que había estudiado un semestre y en la que guardaba buenos contactos; pero la condición de mujer le dificultaba el acceso al puesto.
David Hilbert, Albert Einstein y otros personajes importantes de la historia la consideraban la mujer más importante 🌟 en la historia de la matemática. Sin embargo, ni siquiera eso le garantizó un puesto digno en la universidad por el mero hecho de ser mujer.
¿Te has quedado con ganas de saber más? ¡Mira las clases particulares online matematicas!
Hipatia de Alejandría
Como acabamos de adelantar, Hipatia de Alejandría fue una de las primeras mujeres matemáticas y científicas de la historia, rodeada de grandes tensiones religiosas y culturales, y destacó como maestra 👩🏫 de matemáticas, filosofía y astronomía en la famosa Biblioteca de Alejandría.
Entre sus aportaciones se encuentran trabajos en geometría, álgebra y astronomía, y se dedicó también a comentar y preservar obras clásicas de autores como Euclides, mencionado en este artículo. Hipatia fue ni más ni menos que miembro y cabeza de la Escuela neoplatónica de Alejandría.
Hoy es recordada no solo por sus aportes científicos, sino también por representar la resistencia del saber frente a la intolerancia.

A estas alturas, ya habrás comprendido que la evolución de una ciencia como las matemáticas es y será siempre inseparable de la historia de la Humanidad. A través de los mejores matemáticos de la historia (y matemáticas), podemos observar cómo el pensamiento humano ha pasado de abstracto a revolucionario, conciso y revelador, permitiéndonos comprender el mundo 🌍 y transformar la sociedad.
📚 Bibliografía
- Bell, E. T. (1937). Los grandes matemáticos: Desde Zenón a Poincaré (trad. esp.). Ediciones Paidós.
- Navarro, J. (2019). Mujeres matemáticas. Editorial Nivola.
- Colección Genios de las Matemáticas. (s. f.). Editorial Genios Matemáticas.
- Kasner, E., & Newman, J. R. (1940). Mathematics and the imagination. Simon & Schuster.
Resumir con IA: