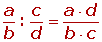Un número racional es todo número que puede representarse como el cociente de dos enteros, con denominador distinto de cero. Se representa por Explicaciones y ejemplos de los números racionales - 1.

Explicaciones y ejemplos de los números racionales - 2

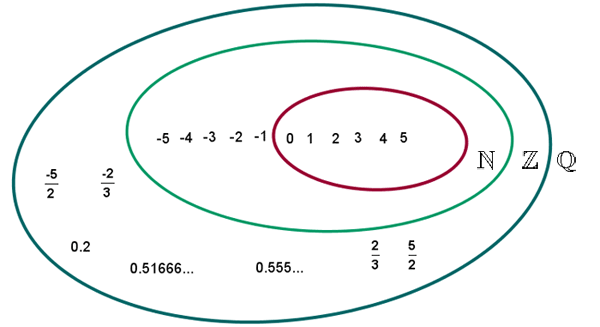
Explicaciones y ejemplos de los números racionales - 3

Representación de números racionales

Los números racionales se representan en la recta junto a los números enteros.

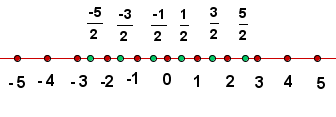
Explicaciones y ejemplos de los números racionales - 4

Para representar con precisión los números racionales:

1

Tomamos un segmento de longitud la unidad, por ejemplo.

2

Trazamos un segmento auxiliar desde el origen y lo dividimos en las partes que deseemos. En nuestro ejemplo, lo dividimos en 4 partes.

3

Unimos el último punto del segmento auxiliar con el extremo del otro segmento y trazamos segmentos paralelos en cada uno de los puntos, obtenidos en la partición del segmento auxiliar.

Explicaciones y ejemplos de los números racionales - 5

En la práctica se utilizan número racional y fracción como sinónimos.

Suma y resta de números racionales

Con el mismo denominador

Se suman o se restan los numeradores y se mantiene el denominador.

Explicaciones y ejemplos de los números racionales - 6

Explicaciones y ejemplos de los números racionales - 7

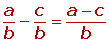
Explicaciones y ejemplos de los números racionales - 8

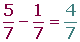
Explicaciones y ejemplos de los números racionales - 9

Con distinto denominador

En primer lugar se reducen los denominadores a común denominador, y se suman o se restan los numeradores de las fracciones equivalentes obtenidas.

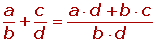
Explicaciones y ejemplos de los números racionales - 10

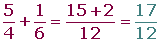
Explicaciones y ejemplos de los números racionales - 11

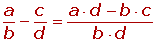
Explicaciones y ejemplos de los números racionales - 12

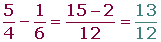
Explicaciones y ejemplos de los números racionales - 13

Propiedades de la suma de números racionales

1.

Interna:

a + b 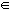Explicaciones y ejemplos de los números racionales - 14 Explicaciones y ejemplos de los números racionales - 15

2.

Asociativa:

(a + b) + c = a + (b + c) ·

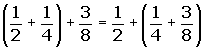
Explicaciones y ejemplos de los números racionales - 16

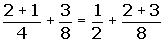
Explicaciones y ejemplos de los números racionales - 17

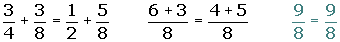
Explicaciones y ejemplos de los números racionales - 18

3.

Conmutativa:

a + b = b + a

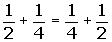
Explicaciones y ejemplos de los números racionales - 19

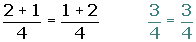
Explicaciones y ejemplos de los números racionales - 20

4.

Elemento neutro:

a + 0 = a

Explicaciones y ejemplos de los números racionales - 21

5.

Elemento opuesto

a + (−a) = 0

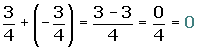
Explicaciones y ejemplos de los números racionales - 22

El opuesto del opuesto de un número es igual al mismo número.

Explicaciones y ejemplos de los números racionales - 23

Multiplicación de números racionales

Explicaciones y ejemplos de los números racionales - 24

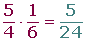
Explicaciones y ejemplos de los números racionales - 25

Propiedades de la multiplicación de números racionales

1.

Interna:

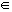
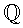
a · b Explicaciones y ejemplos de los números racionales - 26 Explicaciones y ejemplos de los números racionales - 27

2.

Asociativa:

(a · b) · c = a · (b · c)

Explicaciones y ejemplos de los números racionales - 28

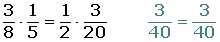
Explicaciones y ejemplos de los números racionales - 29

3.

Conmutativa:

a · b = b · a

Explicaciones y ejemplos de los números racionales - 30

4.

Elemento neutro:

a ·1 = a

Explicaciones y ejemplos de los números racionales - 31

5.

Elemento inverso: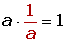

Explicaciones y ejemplos de los números racionales - 32

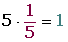
Explicaciones y ejemplos de los números racionales - 33

6.

Distributiva:

a · (b + c) = a · b + a · c

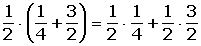
Explicaciones y ejemplos de los números racionales - 34

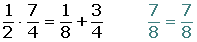
Explicaciones y ejemplos de los números racionales - 35

7.

Sacar factor común:

a · b + a · c = a · (b + c)

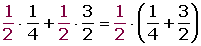
Explicaciones y ejemplos de los números racionales - 36

División de números racionales

Explicaciones y ejemplos de los números racionales - 37