Completa la respuesta de las siguientes sumas y restas de fracciones
 |  |  |  | |
 | | |
Este campo es obligatorio.
Como ambas fracciones tienen el mismo denominador, este se conserva y sumamos los numeradores
 |  |  | | |
 | | |
Este campo es obligatorio.
Como ambas fracciones tienen el mismo denominador, este se conserva y restamos los numeradores
| | | | |
|  |  |
Este campo es obligatorio.
Las fracciones tienen distinto denominador y no se pueden realizar únicamente la suma o resta de numeradores. En estos casos calculamos el mínimo común y múltiplo de los denominadores y
Calculamos fracciones equivalentes a las del problema pero con el mcm como denominador
Realizamos la suma de fracciones con el mismo denominador
| | | | |
|  |  |
Este campo es obligatorio.
Las fracciones tienen distinto denominador y no se pueden realizar únicamente la suma o resta de numeradores. En estos casos calculamos el mínimo común y múltiplo de los denominadores de y
Calculamos fracciones equivalentes a las del problema pero con el mcm como denominador
Realizamos la suma de fracciones con el mismo denominador
| | | | |
 | |
Este campo es obligatorio.
Las fracciones tienen distinto denominador y no se pueden realizar únicamente la suma o resta de numeradores. En estos casos calculamos el mínimo común y múltiplo de los denominadores de y
Calculamos fracciones equivalentes a las del problema pero con el mcm como denominador
Realizamos la suma de fracciones con el mismo denominador
| | | | |
 |  |
Este campo es obligatorio.
Las fracciones tienen distinto denominador y no se pueden realizar únicamente la suma o resta de numeradores. En estos casos calculamos el mínimo común y múltiplo de los denominadores de y
Calculamos fracciones equivalentes a las del problema pero con el mcm como denominador
Realizamos la resta de fracciones con el mismo denominador
| | | | | | |
 | | | |
Este campo es obligatorio.
Como las tres fracciones tienen el mismo denominador, este se conserva y se suman los numeradores
| | | | | | |
| | | |
Este campo es obligatorio.
Como las tres fracciones tienen el mismo denominador, este se conserva y se restan los numeradores
| | | | | | |
 | | |
Este campo es obligatorio.
Como las tres fracciones tienen el mismo denominador, este se conserva y se realizan las operaciones en los numeradores
| | | | | | |
| | |
Este campo es obligatorio.
Como las tres fracciones tienen el mismo denominador, este se conserva y se realizan las operaciones en los numeradores
Observamos que en el resultado anterior, el numerador y denominador son múltiplos de 3, por lo que simplificamos
| | | | | | |
| | |
Este campo es obligatorio.
Las fracciones tienen distinto denominador y no se pueden realizar únicamente la suma o resta de numeradores. En estos casos calculamos el mínimo común y múltiplo de los denominadores de 
y
Calculamos fracciones equivalentes a las del problema pero con el mcm como denominador
Realizamos la suma de fracciones con el mismo denominador
| | | | | | |
| | |
Este campo es obligatorio.
Las fracciones tienen distinto denominador y no se pueden realizar únicamente la suma o resta de numeradores. En estos casos calculamos el mínimo común y múltiplo de los denominadores de 
y
Calculamos fracciones equivalentes a las del problema pero con el mcm como denominador
Realizamos la resta de fracciones con el mismo denominador
| | | | | | |
| | |
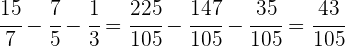
Este campo es obligatorio.
Las fracciones tienen distinto denominador y no se pueden realizar únicamente la suma o resta de numeradores. En estos casos calculamos el mínimo común y múltiplo de los denominadores de 
y
Realizamos la suma y resta de fracciones con el mismo denominador
| | | | | | |
| |  |
Este campo es obligatorio.
Las fracciones tienen distinto denominador y no se pueden realizar únicamente la suma o resta de numeradores. En estos casos calculamos el mínimo común y múltiplo de los denominadores de 
y
Calculamos fracciones equivalentes a las del problema pero con el mcm como denominador
Realizamos la suma y resta de fracciones con el mismo denominador
| | | | | | |
| | |
Este campo es obligatorio.
Las fracciones tienen distinto denominador y no se pueden realizar únicamente la suma o resta de numeradores. En estos casos calculamos el mínimo común y múltiplo de los denominadores de 
y
Calculamos fracciones equivalentes a las del problema pero con el mcm como denominador
Realizamos la suma de fracciones con el mismo denominador
Si tienes dudas puedes consultar la teoría
Resumir con IA:
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Si van a poner ejercicio pónganlo bien si van a poner división póngame en el signo de división si van a poner multiplicación ponga bien el signo de multiplicación
Fracciónes y la unidad que representan problemas de la vida diaria usando las fracciones y las unidades que representan
La mitad y la mitad
En otro problema podemos ver qué está fracciones y litros ahí podemos ver los litros de agua y que tienes que saber cuántos litros de agua quedan
Por lo tanto quedan 90 litros de agua en el tanque
Hola, muchas gracias por tu aportación.
Hola lamentamos los errores cometidos, podrías hacernos el favor de mencionarnos donde están las fallas para poder corregirlas.
En el ejercicio dos no da esa respuesta
Hola el artículo que revise hay varios ejercicios 2, pero no encontré el error que mencionas, podrías dar mas detalles por favor, así se podrá corregir.