La proporcionalidad es un concepto fundamental en matemáticas y en la vida diaria, que nos permite comparar y entender la relación entre diferentes cantidades. En esencia, dos magnitudes son proporcionales cuando su razón o cociente es constante. Este principio se aplica en diversas áreas, desde la resolución de problemas cotidianos hasta situaciones más complejas en campos como la economía, la ingeniería y las ciencias sociales.
Pedro y María invirtieron 100 € durante un año, recibiendo una ganancia de 20 €. Si Pedro proporcionó 45 € para la inversión y María 55 €. ¿Cuánto le corresponde a cada uno si se reparten la ganancia de manera proporcional a lo que invirtieron?
1 Al ser un problema de proporcionalidad directa podemos establecer las siguientes igualdades
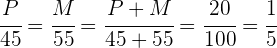
2 Resolviendo para cada incógnita
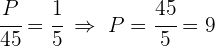
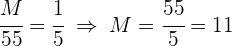
Mario y Juan pintaron una casa y recibieron un pago de 500 €. Si Mario trabajó 10 horas y Juan 15. ¿Cuánto le corresponde a cada uno si se reparte proporcionalmente al tiempo trabajado?
1 Al ser un problema de proporcionalidad directa podemos establecer las siguientes igualdades
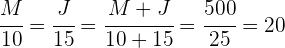
2 Resolviendo para cada incógnita
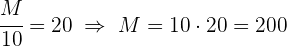
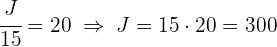
Dos hermanos participan en un concurso donde el primero comete dos errores y el segundo tres. En el concurso ganan 100 € y deciden repartirlo de manera inversamente proporcional al número de errores cometidos, ¿cuánto le corresponde a cada uno?
1 Al ser un problema de proporcionalidad inversa, tomamos las inversas
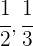
2 Ponemos a común denominador
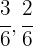
3 Realizamos un reparto directamente proporcional a los numeradores
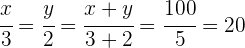
4 Resolviendo para cada incógnita
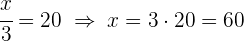
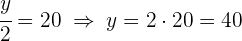
Se reparten 60 € entre dos hermanos de manera inversamente proporcional al número de castigos obtenidos durante una semana. Si el primer hermano tuvo tres castigos y el segundo cinco, ¿cuánto le corresponde a cada uno?
1 Al ser un problema de proporcionalidad inversa, tomamos las inversas
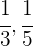
2 Ponemos a común denominador
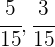
3 Realizamos un reparto directamente proporcional a los numeradores
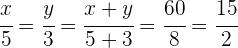
4 Resolviendo para cada incógnita
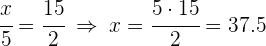
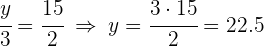
Un abuelo reparte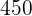 
entre sus tres nietos de 
y 
años de edad; proporcionalmente a sus edades. ¿Cuánto corresponde a cada uno?
1 Al ser un problema de proporcionalidad directa podemos establecer las siguientes igualdades
2 Resolviendo para cada incógnita
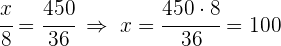
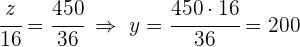
Se asocian tres individuos aportando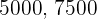 
y 
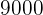. Al cabo de un año han ganado 
. ¿Qué cantidad corresponde a cada uno si hacen un reparto directamente proporcional a los capitales aportados?
1 Al ser un problema de proporcionalidad directa podemos establecer las siguientes igualdades
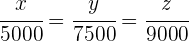
2 Resolviendo para cada incógnita
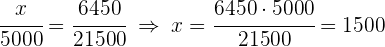
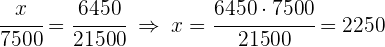
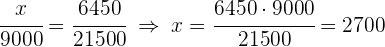
Se reparte una cantidad de dinero, entre tres personas, directamente proporcional a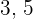 
y 
. Sabiendo que a la segunda le corresponde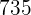 
. Hallar lo que le corresponde a la primera y tercera.
1 Al ser un problema de proporcionalidad directa podemos establecer las siguientes igualdades
2 Calculamos las incógnitas faltantes
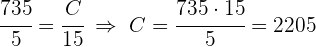
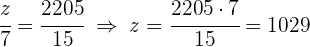
Se reparte dinero en proporción a 
y 
; al menor le corresponden 
. ¿Cuánto corresponde a los otros dos?
1 Planteamos las igualdades de la proporcionalidad directa y calculamos las incógnitas faltantes
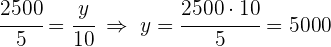
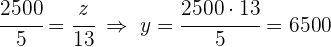
Tres hermanos ayudan al mantenimiento familiar entregando anualmente 5900 €. Si sus edades son de 20, 24 y 32 años y las aportaciones son inversamente proporcionales a la edad, ¿cuánto aporta cada uno?
1 Al ser un reparto inversamente proporcional, tenemos que tomar las inversas de las edades
2 Ponemos a común denominador
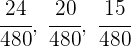
3 Realizamos un reparto directamente proporcional a los numeradores: 
y 
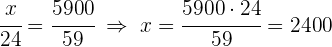
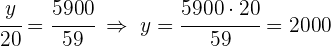
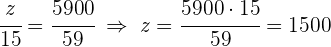
Repartir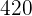 
, entre tres niños en partes inversamente proporcionales a sus edades, que son 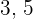y 
.
1 Al ser un reparto inversamente proporcional, tenemos que tomar las inversas de las edades
2 Ponemos a común denominador
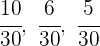
3 Realizamos un reparto directamente proporcional a los numeradores: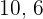 
y 
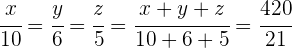
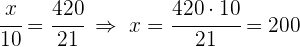
¿Durante cuánto tiempo ha de imponerse un capital de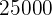 
al 
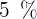para que se convierta en 
?
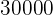1 Calculamos el interés obtenido:
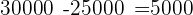
años
Se prestan 
y al cabo de un año, 
meses y 
días se reciben 
. Calcular el tanto por ciento de interés.
1 Calculamos el tiempo en días
días
2 Calculamos el interés
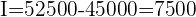
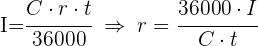
3 Calculamos el rédito
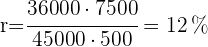
Hallar él tanto por ciento de interés simple al que deberá prestarse un capital para que al cabo de años los intereses sean equivalentes al capital prestado.
1 El interés es igual al capital
2 Sustituimos en 
por la fórmula del interés
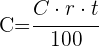
3 Productos de extremos es igual a producto de medios
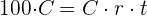
4 Si tenemos 
, entonces 
. De este modo podemos despejar el rédito
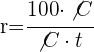
5 Simplificamos la fracción
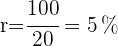
¿En cuánto tiempo se duplica un capital colocado al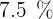 
?
1El interés es igual al doble del capital
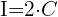
2Sustituimos el interés por su fórmula, despejamos el tiempo y simplificamos
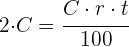
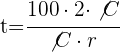
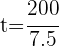
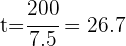años.
¿En cuánto tiempo se triplica un capital colocado al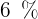 
?
1El interés es igual al triple del capital
2Sustituimos el interés por su fórmula, despejamos el tiempo y simplificamos
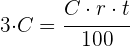
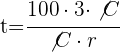
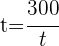
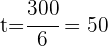años.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Cuánto se debe depositar cada fin de semestre si usted quiere acumular Bs 10000 al cabo de 4 años conociendo que la entidad financiera reconoce un interés del 12% anual
esta mal la mayoria de ejercicios la cual se confunde en el mismo ejercicios ep e ip
Hola puedes hacernos el favor de mencionar los ejercicios que están mal para poder corregirlos y así evitar confusiones.
Buenos días, el ejercicio 1 está mal si la relación fuera directa entre las variables que no lo e como muestra ahí daría 400kg. La respuesta para mí es que: la relación de las variables es indirecta lo que no sé cómo llega a los 25000. No llego a ese número.
La empresa A1 tal pone en la bolsa de valores $134 acciones por 130 c/u para mantenerlas 3 años
La empresa A2 las compra y las pone nuevamente en la bolsa de valores a un interes simple de 30% por los 3 años
La tercera empresa compra estas acciones por 5 años
Durante el primer semestre la empresa A2 ve que las acciones compradas bajan a $100 podría resolverlo con las cuentas
Hola tu razonamiento es correcto si a mayor tamaño de la rueda, mas vueltas da, pero no es así, pues las ruedas grandes dan menos vueltas que las ruedas pequeñas, por eso se usa razones inversamente proporcionales.