Resuelve los siguientes problemas utilizando el algoritmo de Euclides:
María prepara una cena especial para su familia. Ha hecho 56 canapés de queso y 40 de paté. Quiere repartir los canapés en el máximo número de platos posibles, de manera que haya el mismo número de canapés de cada tipo en todos los platos. ¿Cuántos platos necesitará?
platos.
Este campo es obligatorio.
1 El número de platos deberá ser divisor de 56 y de 40. Además deberá ser el máximo divisor común a ambos
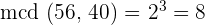
2 El número máximo de platos es 8
3 En cada plato habrá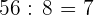 
canapés de queso y 
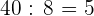canapés de paté.
2Se quiere alicatar la pared de una cocina con azulejos cuadrados. Sabemos que la pared mide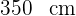 
de ancho por 
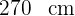de alto. Si queremos que los azulejos sean del mayor tamaño posible, ¿cuál debe ser la medida del lado de cada azulejo y la cantidad total de ellos?
lado = 
.
Este campo es obligatorio.
Total de azulejos=
Este campo es obligatorio.
1 El lado de cada azulejo deberá ser divisor de 350 y de 270. Además deberá ser el máximo divisor común a ambos
2 El lado de cada azulejo mide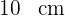 
3 Para cubrir el ancho se requiere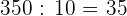 
azulejos y 
azulejos para cubrir el alto.
4 El total de azulejos requeridos es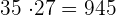 
3María tiene 36 malvaviscos y 40 paletas las cuales divide en bolsas que contienen una misma cantidad de malvaviscos y una misma cantidad de paletas. ¿Cuántas bolsas puede llenar y que cantidad de dulces contiene cada bolsa?
bolsas.
Este campo es obligatorio.
malvaviscos.
Este campo es obligatorio.
paletas.
Este campo es obligatorio.
1 El número de bolsas deberá ser divisor de 36 y de 40. Además deberá ser el máximo divisor común a ambos
2 El número máximo de bolsas es 4
3 En cada bolsa habrá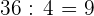 
malvaviscos y 
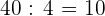paletas.
4Un granjero tiene 18 gallinas, 72 cerdos y 45 ovejas. ¿Cuántos establos requiere construir para que en cada uno se tenga la misma cantidad de animales de cada tipo?
establos.
Este campo es obligatorio.
gallinas.
Este campo es obligatorio.
cerdos.
Este campo es obligatorio.
ovejas.
Este campo es obligatorio.
1 El número de establos deberá ser divisor de 18, de 72 y de 45. Además deberá ser el máximo divisor común
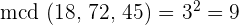
2 El número máximo de establos es 9
3 En cada establo habrá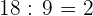 
gallinas, 
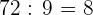cerdos, y 
ovejas.
5 se requiere construir un ortoedro de medidas 110, 132 y 165 centímetros empleando cubos de volumen máximo. ¿Cuántos cubos se requieren y cual es la medida de su arista?
Arista = .
Este campo es obligatorio.
Total de cubos =
Este campo es obligatorio.
1 La medida de la arista de los cubos deberá ser divisor de 110, de 132 y de 165. Además deberá ser el máximo divisor común
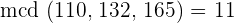
2 Para cubrir los distintos lados se requiere: 
cubos.
3 El total de cubos requeridos es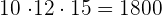 
6Pedro tiene 51 galletas, 34 paletas y 85 caramelos, y los quiere distribuir entre el máximo número de personas de manera que cada una tenga la misma cantidad de cada tipo. ¿Entre cuántas personas podrá distribuir sus galletas y dulces? ¿Cuánto le tocará a cada persona?
personas.
Este campo es obligatorio.
galletas.
Este campo es obligatorio.
paletas.
Este campo es obligatorio.
caramelos.
Este campo es obligatorio.
1 El número de personas deberá ser divisor de 51, de 34 y de 85. Además deberá ser el máximo divisor común
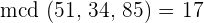
2 El número máximo de personas es 17
3 A cada persona le tocará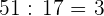 
galletas, 
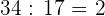paletas, y 
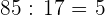caramelos.
Si tienes dudas puedes consultar la teoría
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
buen dia, creo la respuesta del ejercicio 3 esta mal planteada: María no tiene 18 alumnos, 18 es la cantidad máxima de dulces repartidos a cada uno, en si, ella tiene solo 5 alumnos (5*18=90dulces en total)
Hola tu razonamiento es bueno, pero si pueden ser 18 alumnos, pues se pueden repartir de 2 paletas (2*18=36) y 3 caramelos (3*18=54).
EJERCICIOS INTERACTIVOS DE MULTIPLOS
Hola podrías hacernos el favor de mencionarnos en que ejercicio esta el error para poder corregirlo.
cual es 15 -18
Hola el ejercicio que aparece es el de encontrar el MCD y MCM de 72, 108 y 72, también con los números 1048, 786 y 3930, lo revise y no encontré el error, si me equivoco de artículo menciónalo por favor.
A mi también el de la cantidad de divisor es de un número(en el ejercicio 8)