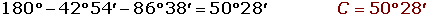Un triángulo es oblicuángulo si no es recto ninguno de sus ángulos,
En la resolución de triángulos oblicuángulos vamos a utilizar los teoremas del seno y del coseno.
Hay cuatro casos de resolución de triángulos oblicuángulos:
1º. Conociendo un lado y dos ángulos adyacentes a él



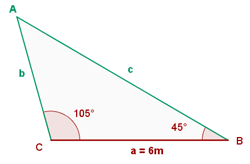
De un triángulo sabemos que: a = 6 m, B = 45° y C = 105°. Calcula los restantes elementos.
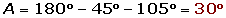

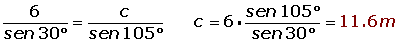
2º. Conociendo dos lados y el ángulo comprendido



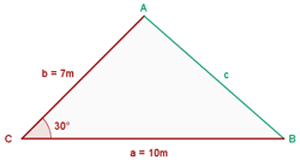
De un triángulo sabemos que: a = 10 m, b = 7 m y C = 30°. Calcula los restantes elementos.
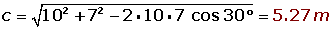

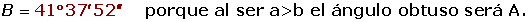
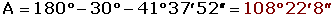
3º Conociendo dos lados y un ángulo opuesto

sen B > 1. No hay solución
sen B = 1 Triángulo rectángulo
sen B < 1. Una o dos soluciones

Supongamos que tenemos a, b y A; al aplicar el teorema de los senos puede suceder:
1. sen B > 1. No hay solución.
Resuelve el triángulo de datos: A = 30°, a = 3 m y b = 8 m.

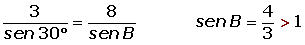
Como el seno de un ángulo nunca puede ser mayor que 1, el problema no tiene solución. La figura muestra la imposibilidad de que exista el triángulo planteado.
2. sen B = 1. Solución única: triángulo rectángulo
Resuelve el triángulo de datos: A = 30°, a = 3 m y b = 6 m.


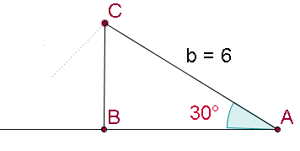
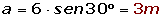

3. sen B < 1. Una o dos soluciones
Resuelve el triángulo de datos: A = 60°, a = 8 m y b = 4 m.
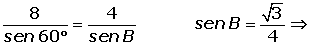
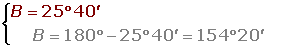
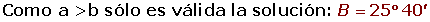

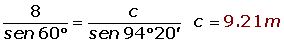
Resuelve el triángulo de datos: A = 30°, a = 3 m y b = 4 m.






4º. Conociendo los tres lados
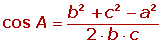
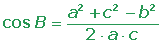

Resuelve el triángulo de datos: a = 15 m, b = 22 m y c = 17 m.