Elige la opcion correcta:
Un árbol y una persona se encuentran en orillas opuestas de un río. Esta persona observa el punto más alto del árbol bajo un ángulo de 40º. Si retrocede 15 m y vuelve a medir el ángulo, obtiene 20º. ¿Cuál es la altura del árbol y la anchura del río?
Selecciona una respuesta.
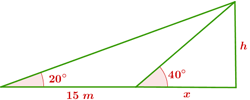
1Usamos las razones trigonométricas apropiadas en cada uno de los dos triángulos rectángulos
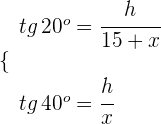
2Escribimos sin denominadores
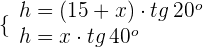
3Igualamos ambas ecuaciones y resolvemos

4Calculamos la altura del árbol
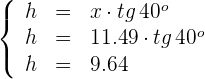
5El árbol mide 9.64 metros de altura y la anchura del río es de 11.49 metros
Eva observa desde la ventana de su casa un accidente con un ángulo de 60º. Como es muy curiosa y desde allí no lo ve muy bien, sube a la azotea del edificio que está 15 metros más arriba. Coge unos prismáticos y ahora ve el accidente con un ángulo de 35º. ¿Qué altura tiene el edificio y a qué distancia de casa de Eva ocurrió el accidente?
Selecciona una respuesta.
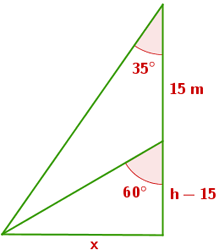
1Usamos las razones trigonométricas apropiadas en cada uno de los dos triángulos rectángulos
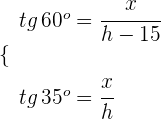
2Escribimos sin denominadores

3Igualamos ambas ecuaciones y resolvemos
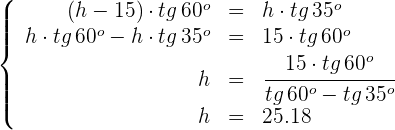
4Calculamos la distancia
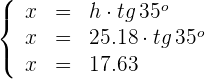
5El edificio tiene una altura de 25.18 metros. El accidente ocurrió a una distancia de 17.63 metros de casa de Eva
Un barco se encuentra en cierto punto del mar. La situación de los viajeros es dramática ya que en este momento les queda combustible para recorrer 400 metros. El capitán del barco observa en este punto la luz de un faro con un ángulo de elevación de 8º. Después de recorrer 250 metros en dirección hacia el faro, el ángulo que forma la luz con la horizontal del mar es ahora de 22º. ¿Qué altura tiene el faro? ¿Llegará el barco a tierra?
Selecciona una respuesta.

1Usamos las razones trigonométricas apropiadas en cada uno de los dos triángulos rectángulos
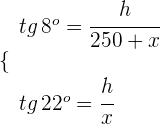
2Escribimos sin denominadores
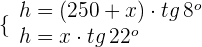
3Igualamos ambas ecuaciones y resolvemos

4Calculamos la altura del faro
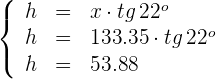
5El faro tiene 53.88 metros de altura
.
Al principio, el barco tenía combustible para recorrer 400 metros. Después de recorrer, 250 metros, le queda combustible para recorrer 400 − 250 = 150 metros. Pero hemos calculado que desde este punto hasta la orilla hay 133.35, así que el barco llegará a tierra
.
En una carretera de montaña nos encontramos con una señal que indica un 25% de pendiente. ¿Qué ángulo forma este tramo de la carretera con la horizontal? Si hemos recorrido 5 km por esta carretera, ¿cuántos metros hemos ascendido?
Selecciona una respuesta.

1Calculamos el ángulo que forma la carretera con la horizontal

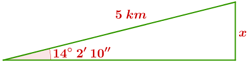
2Calculamos los metros ascendidos
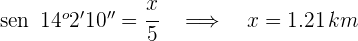
Realiza: (Redondea a dos decimales en el caso que sea necesario)
Si buscas un maestro de matematicas, no dudes en consultar nuestra plantilla de Superprofes.
En cierta ciudad están de obras. La distancia entre dos grúas es de 120 metros. Nos situamos en un punto que se encuentra entre las dos grúas(no necesariamente en el punto medio). Desde aquí observamos el punto más alto de las grúas y vemos que los ángulos que se forman con la horizontal son de 35º y 23º. Si las dos grúas miden lo mismo, ¿cuál es su altura?
Altura = m
Este campo es obligatorio.

1Usamos las razones trigonométricas apropiadas en cada uno de los dos triángulos rectángulos
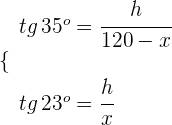
2Escribimos sin denominadores

3Igualamos ambas ecuaciones y resolvemos
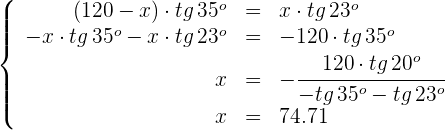
4Calculamos la altura

5La altura de ambas grúas es de 31.71 metros
Calcula la altura del cuerpo más alto:
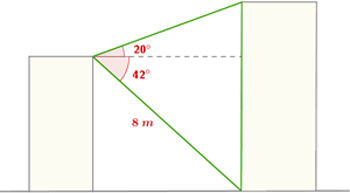
Altura = m
Este campo es obligatorio.
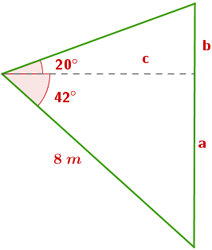
1Para calcular el valor de  aplicamos
aplicamos

2Para calcular  , primero necesitamos calcular
, primero necesitamos calcular 

3Calculamos 
4La altura del cuerpo más alto es 5.35 + 2.17 = 7.52 metros
Se puede acceder a una mina descendiendo 500 metros por un ascensor vertical o por un camino de 950 metros que tiene un ángulo de inclinación de 20º tal y como muestra la figura. ¿Qué diferencia de altura hay entre las dos entradas a la mina?
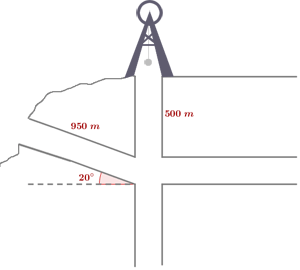
Diferencia de altura = m
Este campo es obligatorio.
1Calculamos la altura  del camino
del camino
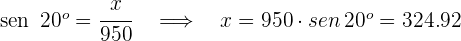
2Calculamos la diferencia de alturas
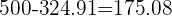
3Entre las dos entradas a la mina hay una diferencia de altura de 175.08 metros
Calcular el lado de un pentágono regular inscrito en una circunferencia de 8 cm de radio
Lado = cm
Este campo es obligatorio.

1Unimos el centro de la circunferencia con los vértices del pentágono, con lo que éste queda dividido en cinco triángulos iguales. Nos quedamos con uno de estos triángulos: el triángulo  .
.
2Como la circunferencia tiene  , el ángulo
, el ángulo  por ser un ángulo central del pentágono tiene
por ser un ángulo central del pentágono tiene
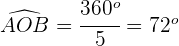
3Trazamos la apotema  , de manera que el triángulo
, de manera que el triángulo  queda dividido en dos triángulos iguales
queda dividido en dos triángulos iguales 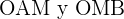 .
.
4Consideramos el triángulo 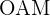 :
:

5El ángulo 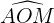 tiene entonces
tiene entonces
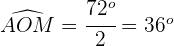
6Calculamos la longitud del lado 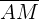 :
:

7Esta longitud es la mitad del lado del pentágono, así que el lado del pentágono tiene una longitud de 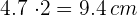
Si tienes dudas puedes consultar la teoría
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Cálculo el lado bc aplicando la ley de cosenos b=5cm c=6cm a=60°
Materia:
erica V= 1
Calcula el lado BC aplicando
5
V
0
V
4
V
A
B
AB = 6cm
CR
Datos
0 =5cm
C=600
En un triángulo, se tienen los datos: A = 50° ,B = 65° y a = 12. Encuentra el lado b.
excelente, por ejemplo tengo uno donde me hacen falta el ángulo A, B, C tengo estos datos lado a:14, b:6, c:4
La respuesta es 14.197
¿ porqué no hay un modo de resolver triángulos sin la necesidad de aplicar la Trigonometria académica ? Saludos, profesor.
Hola, posiblemente exista otro método, pero por desgracia es todavía mas difícil que la trigonometría académica incluso te puedo asegurar que hoy en día es mas fácil y mas directo resolver los problemas de triángulos, entendemos que a veces llega a ser confuso pero te aseguramos que este método es el mas sencillo que existe.
Resuelve esto bien y claro.
¿Cuánto le falta al complemento del suplemento de 165,315° para alcanzar el suplemento del complemento de π/12 rad?
como resolver este ejercicio (tag x )2 -1
_________= -(tag x )2
(cotag x )2 -1