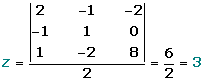La condición necesaria y suficiente para que un sistema de m ecuaciones y n incógnitas tenga solución es que el rango de la matriz de los coeficientes y el de la matriz ampliada sean iguales.

  • r = r'Sistema Compatible.
    • r = r'= nSistema Compatible Determinado.
    • r = r'≠ nSistema Compatible Indeterminado.
  • r ≠ r'Sistema Incompatible.

Ejemplo

Explicaciones y ejemplos de teorema de rouché-fröbenius - 1

1.

Tomamos la matriz de los coeficientes y le hallamos el rango.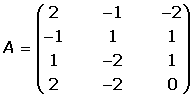

Explicaciones y ejemplos de teorema de rouché-fröbenius - 2

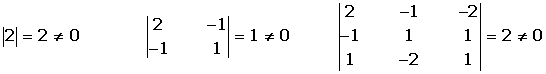
Explicaciones y ejemplos de teorema de rouché-fröbenius - 3

r(A) = 3

2.

Hallamos el rango de la matriz ampliada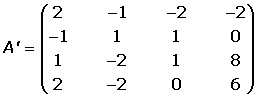

Explicaciones y ejemplos de teorema de rouché-fröbenius - 4

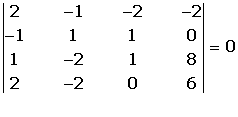
Explicaciones y ejemplos de teorema de rouché-fröbenius - 5

r(A') = 3

3.

Aplicamos el teorema de Rouché.

Explicaciones y ejemplos de teorema de rouché-fröbenius - 6

Explicaciones y ejemplos de teorema de rouché-fröbenius - 7

4.

Se resuelve el sistema, si éste no es incompatible, por la regla de Cramer o por el método de Gauss

Tomamos el sistema que corresponde a la submatriz de orden 3, que tiene rango 3, y lo resolvemos.

Explicaciones y ejemplos de teorema de rouché-fröbenius - 8

Explicaciones y ejemplos de teorema de rouché-fröbenius - 9

Explicaciones y ejemplos de teorema de rouché-fröbenius - 10