29 junio 2021
Pierre Sarrus (1798, 1861) fue un matemático francés que estableció una regla para calcular
determinantes de orden 3.
Que es la Regla de Sarrus
La regla de Sarrus es un proceso o algoritmo para calcular el determinante de una matriz de 
.
Este proceso es sencillo y facil de memorizar y lo describieremos a continuación.
Dada una matriz
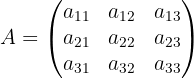
a continuación describimos dicho proceso para calcular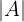 
.
Paso 1: Formar una nueva matriz de 5 filas, repitiendo las dos primeras filas debajo de la
matriz inicial
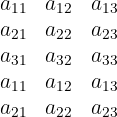
Paso 2: Identificar los sumandos positivos. Estos estan dados por:
El producto de los elementos en la diagonal principal de la matriz
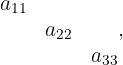
el producto de los elementos en la diagonal que esta debajo de la diagonal principal de la
matriz
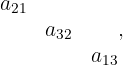
y el producto de los elementos en la diagonal siguiente debajo a las anteriores diagonales.
Paso 3. Identificar los sumandos negativos. Éstos son,El producto de los elementos en la diagonal secundaria de la matriz.
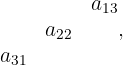
el producto de los elementos en la diagonal que esta debajo de la diagonal secundaria
de la matriz.
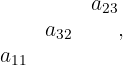
y el producto de los elementos en la diagonal siguiente debajo a las anteriores diagonales.
Paso 4. Realizar la suma de los términos positivos más los términos negativos que hemos identificado en los pasos anteriores. Esto nos da como resultado el determinante que buscamos: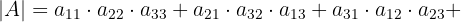
[latex]$$(-a_{13}\cdot a_{22}\cdot a_{31}-a_{23}\cdot a_{32}\cdot a_{11}-a_{33}\cdot a_{12}\cdot a_{21}).$$[/latex]
Aplicaciones
Las matrices de son de las más comunes en algebra lineal y calcular su determinante es algo de vital importancia. Generalmente se tiene sistemas de tres ecuaciones con tres incógnitas, una de las formas de saber si dicho sistema tiene solución única o no, es calculando el determinante de la matriz asociada. Es aquí donde la Regla de Sarrus es útil por su sencillez y efectividad.
Ejemplos
1 Calcular el determinante de la siguiente matriz
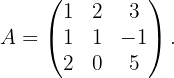
Las diagonales que nos darán términos positivos son las siguientes
Y las diagonales que nos darán términos negativos son las siguientes
Finalmente utilizando la regla de Sarrus obtenemos que
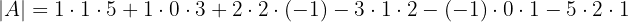
2 Argumentar si la siguiente matriz es invertible o no.
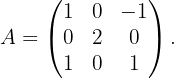
Recordemos que una matriz es invertible sí y sólo sí su determinante es distinto de cero. Así, debemos calcular el determinante de 
Las diagonales que nos darán términos positivos son las siguientes
Y las diagonales que nos darán términos negativos son las siguientes
Finalmente utilizando la regla de Sarrus obtenemos que
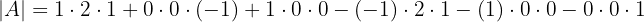
Por lo tanto concluimos que la matriz sí es invertible.
¿Te ha gustado el artículo?
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.