Calcular la inversa de una matriz

Se dice que una matriz cuadrada es invertible si existe una matriz con la propiedad de que

donde es la matriz identidad . La matriz es única, la llamamos la inversa de y la denotamos por Esto es,

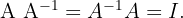
Observación importante: Una matriz es invertible si y sólo si su determinante es distinto de cero. Esto es, una matriz tiene inversa si su determinante es no cero.

La inversa de una matriz satisface las siguientes propiedades:

1 Sean y matrices invertibles del mismo orden, entonces el producto 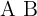es invertible y además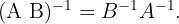

2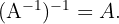

3 Sea un número real no cero, entonces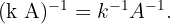

4 Si 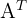denota la transpuesta de una matriz, entonces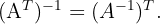

• La matriz inversa es una herramienta importante en la resolución de sistemas de ecuaciones lineales puesto que cualquier sistema puede ser escrito en la forma
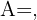  donde es la matriz de coeficientes del sistema, es la matriz columna o vector columna que contiene a las variables "desconocidas" y es la matriz columna cuyas entradas son las constantes al lado derecho de las ecuaciones en el sistema. Por ejemplo, el sistema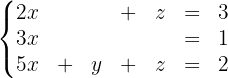

  puede ser expresado como la ecuación matricial 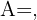donde
  

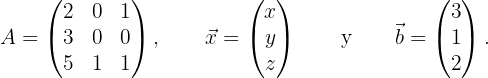
  Dado que la matriz de coeficientes es cuadrada, puede ser invertible. Si es invertible y tenemos una forma de calcular su inversa , entonces podemos determinar por simplemente una multiplicación de matrices
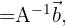  dado que 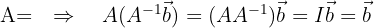resolviendo el sistema de ecuaciones. Así que, una buena aplicación de la inversa de una matriz es la resolución eficiente de sistemas de ecuaciónes lineales.

• Recordemos que, la matriz transpuesta de una matriz de denota por 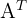y se obtiene cambiando sus filas por columnas (o viceversa). Por ejemplo, continuando con la matriz de arriba tenemos que, si
  
  Se puede calcular la matriz inversa por dos métodos: por el método de Gauss y por el método de adjunción. En este último es donde aparece la matriz transpuesta. Así, la mayor aplicación práctica de la matriz transpuesta es cálculo de la matriz inversa.

Ya hemos estudiado el método de Gauss en otro artículo, ahora centraremos nuestra atención en el método por adjunción.

El cálculo de una matriz inversa por el método de adjunción se basa en el siguiente resultado:

donde

Para entender el procedimiento, veamos un ejemplo:

Ejemplo: Calcular la inversa de la matriz 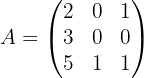que corresponde a los coeficientes del sistema de ecuaciones lineales de arriba.

Solución:

Para calcular la inversa debemos seguir los siguientes pasos:

1 Calculamos el determinante de la matriz:

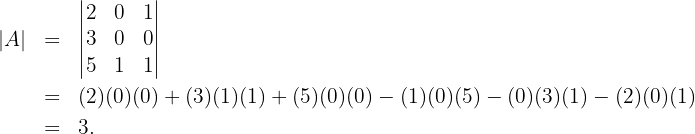
Dado que el determinante no es cero, la matriz tiene inversa.

2 Hallamos la matriz adjunta: Es aquella en la que cada elemento se sustituye por su adjunto.

Esto es,

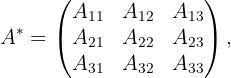
donde

Así

Por lo tanto tenemos que

3 Calculamos la transpuesta de la matriz adjunta: Si

4 La matriz inversa es igual a la transpuesta de la matriz adjunta entre el determinante de la matriz original: Esto es,

Por lo tanto

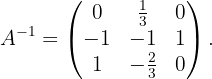
Así, hemos obtenido la inversa de la matriz .

Observación: Como comentario final, podemos resolver el sistema de ecuaciones lineales previamente planteado haciendo
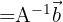obteniendo que

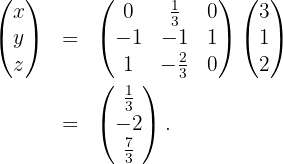
Entonces, la elección de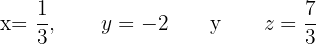
resuelven el sistema anteriormente planteado, como se puede verificar sencillamente.