Capítulos
¡Bienvenidos a la sección de Ejercicios de Ecuaciones Matriciales!
Las ecuaciones matriciales son una herramienta poderosa en álgebra lineal, permitiéndonos expresar y resolver sistemas de ecuaciones de manera eficiente. En esta serie de ejercicios, nos sumergiremos en el mundo de las matrices y exploraremos cómo las ecuaciones matriciales nos ayudan a modelar y resolver problemas en diversas disciplinas.
A lo largo de estos ejercicios, abordaremos la notación matricial, la suma y multiplicación de matrices, y cómo representar sistemas de ecuaciones lineales usando matrices. La capacidad de resolver ecuaciones matriciales es una habilidad esencial con aplicaciones prácticas en diversos campos, desde la ingeniería hasta la física y más allá.

Ecuaciones con Matrices
Dadas las matrices:

Resolver la ecuación:

1 Revisamos si matriz  tiene inversa. Una matriz es invertible si su determinante es distinto de cero, por lo que procedemos a calcular el determinante de la matriz
tiene inversa. Una matriz es invertible si su determinante es distinto de cero, por lo que procedemos a calcular el determinante de la matriz 

Esto nos dice que la matriz  es invertible.
es invertible.
2 Calcular la matriz inversa de  .
.
La formula para calcular la matriz inversa es la siguiente:

donde

La matriz adjunta en este caso es:
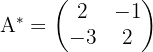
Mientras que la matriz traspuesta de la adjunta es:
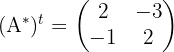
Por lo que la si hacemos el calculo, la matriz inversa de  es:
es:

3 Usar algebra de matrices para reescribir la ecuación.
Dado que  tiene inversa, entonces podemos multiplicar por
tiene inversa, entonces podemos multiplicar por  , a ambos lados de la ecuación por el "lado izquierdo" de la siguiente manera para obtener:
, a ambos lados de la ecuación por el "lado izquierdo" de la siguiente manera para obtener:


Donde  representa la matriz identidad (en este caso de
representa la matriz identidad (en este caso de ).
).
4 Sustituir los valores encontrados y resolver la ecuación.
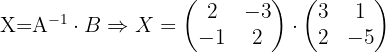

Dadas las matrices:

Resolver la ecuación:

1 Usar algebra de matrices para reescribir la ecuación. Primero hay que despejar  en la ecuación, por lo que hacemos:
en la ecuación, por lo que hacemos: 
2 Calcular la matriz inversa de  .Primero revisaremos que
.Primero revisaremos que  sea invertible, por lo que necesitamos calcular el determinante que es:
sea invertible, por lo que necesitamos calcular el determinante que es:
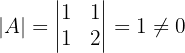
Esto nos dice que la matriz  es invertible.
es invertible.
La matriz inversa de  esta dada por:
esta dada por:

donde

Por lo que haciendo los cálculos obtenemos:
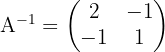
3 Sustituir los valores encontrados y resolver la ecuación:
Tenemos la ecuación:

Sustituyendo los valores de  ,
,  y
y  tenemos:
tenemos:
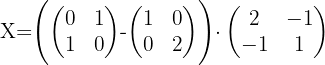
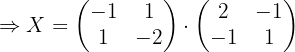

Dadas las matrices:

Resolver la ecuación:

1 Revisamos si matriz  tiene inversa. Una matriz es invertible si su determinante es distinto de cero, por lo que procedemos a calcular el determinante de la matriz
tiene inversa. Una matriz es invertible si su determinante es distinto de cero, por lo que procedemos a calcular el determinante de la matriz 
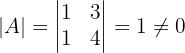
Esto nos dice que la matriz  es invertible.2 Calcular la matriz inversa de
es invertible.2 Calcular la matriz inversa de  .La formula para calcular la matriz inversa es la siguiente
.La formula para calcular la matriz inversa es la siguiente
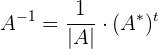
donde

La matriz adjunta en este caso es:
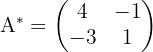
Mientras que la matriz traspuesta de la adjunta es:
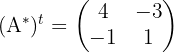
Por lo que la si hacemos el calculo, la matriz inversa de  es:
es:
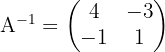
3 Usar algebra de matrices para reescribir la ecuación.
Dado que  tiene inversa, entonces podemos multiplicar por
tiene inversa, entonces podemos multiplicar por  , a ambos lados de la ecuación por el "lado izquierdo" de la siguiente manera para obtener:
, a ambos lados de la ecuación por el "lado izquierdo" de la siguiente manera para obtener:


Donde  representa la matriz identidad (en este caso de
representa la matriz identidad (en este caso de ).
).
4 Sustituir los valores encontrados y resolver la ecuación.
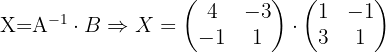
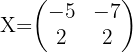
Dadas las matrices:

Resolver la ecuación:

1 Revisamos si matriz  tiene inversa. Una matriz es invertible si su determinante es distinto de cero, por lo que procedemos a calcular el determinante de la matriz
tiene inversa. Una matriz es invertible si su determinante es distinto de cero, por lo que procedemos a calcular el determinante de la matriz 
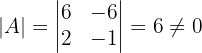
Esto nos dice que la matriz  es invertible.2 Calcular la matriz inversa de
es invertible.2 Calcular la matriz inversa de  .La formula para calcular la matriz inversa es la siguiente:
.La formula para calcular la matriz inversa es la siguiente:

donde

La matriz adjunta en este caso es:
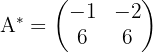
Mientras que la matriz traspuesta de la adjunta es:
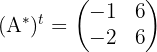
Por lo que la si hacemos el calculo, la matriz inversa de  es:
es:
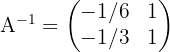
3 Usar algebra de matrices para reescribir la ecuación.
Dado que  tiene inversa, entonces podemos multiplicar por
tiene inversa, entonces podemos multiplicar por  , a ambos lados de la ecuación por el "lado izquierdo" de la siguiente manera para obtener:
, a ambos lados de la ecuación por el "lado izquierdo" de la siguiente manera para obtener:


Donde  representa la matriz identidad (en este caso de
representa la matriz identidad (en este caso de ).
).
4 Sustituir los valores encontrados y resolver la ecuación.
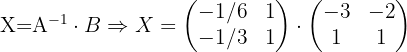
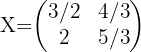
Dadas las matrices:

Resolver la ecuación:

1 Revisamos si matriz  tiene inversa. Una matriz es invertible si su determinante es distinto de cero, por lo que procedemos a calcular el determinante de la matriz
tiene inversa. Una matriz es invertible si su determinante es distinto de cero, por lo que procedemos a calcular el determinante de la matriz 
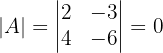
Esto nos dice que la matriz  no es invertible, por lo que no existe una solución.
no es invertible, por lo que no existe una solución.
Resuelve las siguientes ecuaciones, conociendo 3 matrices
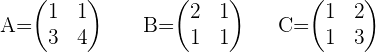
Calcular el valor de  en las siguientes ecuaciones:
en las siguientes ecuaciones:


1 Usar algebra de matrices para reescribir la ecuación.
Primero hay que despejar  de la ecuación, por lo que hacemos:
de la ecuación, por lo que hacemos:
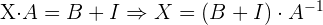
Donde  denota la matriz identidad (de
denota la matriz identidad (de  en este caso).
en este caso).
2 Calcular la matriz inversa de  .
.
Primero revisaremos que  sea invertible, por lo que necesitamos calcular el determinante que es:
sea invertible, por lo que necesitamos calcular el determinante que es:
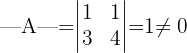
Esto nos dice que la matriz  es invertible.
es invertible.
La matriz inversa de  esta dada por:
esta dada por:
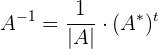
donde

Por lo que haciendo los cálculos obtenemos:
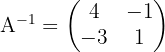
3 Sustituir los valores encontrados y resolver la ecuación:
Tenemos la ecuación:
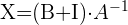
Sustituyendo los valores de  ,
,  y
y  tenemos:
tenemos:
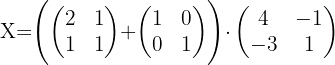
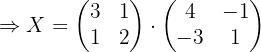
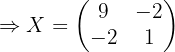


1 Usar algebra de matrices para reescribir la ecuación.
Primero hay que despejar  de la ecuación, por lo que hacemos:
de la ecuación, por lo que hacemos:

2 Calcular la matriz inversa de  .
.
Del ejercicio  tenemos que la matriz inversa de
tenemos que la matriz inversa de  es:
es:
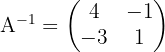
3 Sustituir los valores encontrados y resolver la ecuación:
Tenemos la ecuación:

Sustituyendo los valores de  ,
,  y
y  tenemos:
tenemos:

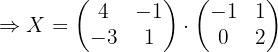
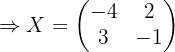


1 Usar algebra de matrices para reescribir la ecuación.
Primero hay que despejar  de la ecuación, por lo que hacemos:
de la ecuación, por lo que hacemos:

2 Calcular la matriz inversa de  .
.
Del ejercicio  tenemos que la matriz inversa de
tenemos que la matriz inversa de  es:
es:
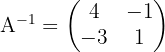
3 Sustituir los valores encontrados y resolver la ecuación:
Tenemos la ecuación:

Sustituyendo los valores de  ,
,  y
y  tenemos:
tenemos:
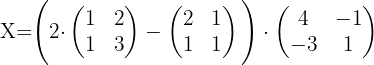
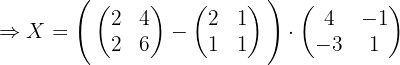
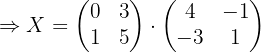
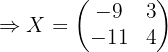

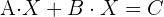
1 Usar algebra de matrices para reescribir la ecuación.
Primero hay que despejar  de la ecuación, por lo que hacemos:
de la ecuación, por lo que hacemos:

2 Calcular la matriz inversa de 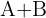 .
.
Primero tenemos que hacer la suma de las matrices  y
y  , la cual es:
, la cual es:
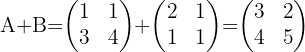
La inversa de una matriz  esta dada por la formula:
esta dada por la formula:

donde

Por lo que si hacemos los cálculos obtenemos que la matriz inversa de 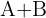 es:
es:
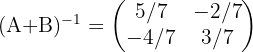
3 Sustituir los valores encontrados y resolver la ecuación:
Tenemos la ecuación:

Sustituyendo los valores de 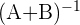 y
y  tenemos:
tenemos:
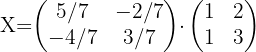
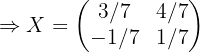


1 Usar algebra de matrices para reescribir la ecuación.
Primero hay que despejar  de la ecuación, por lo que hacemos:
de la ecuación, por lo que hacemos:

2 Encontrar la matriz dada por 
Si sustituimos el los valores de  ,
,  y
y  y realizamos las operaciones correspondientes tenemos:
y realizamos las operaciones correspondientes tenemos:
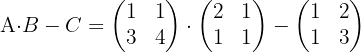
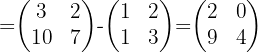
3 Encontrar la matriz inversa de  .
.
Antes de encontrar la matriz inversa, tenemos que verificar que sea invertible. Para esto necesitamos calcular su determinate.

Lo que nos dice que  es invertible. Ahora la inversa de una matriz
es invertible. Ahora la inversa de una matriz  esta dada por la formula:
esta dada por la formula:

donde

Por lo que en este caso si hacemos los cálculos deberíamos de obtener que:

4 Sustituir los valores encontrados y resolver la ecuación:
Tenemos la ecuación:
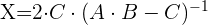
Sustituyendo los valores de 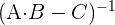 y
y  tenemos:
tenemos:
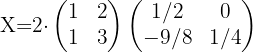
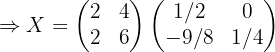
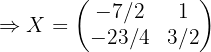
Ecuaciones matriciales
Dadas las matrices:

Resolver las ecuaciones:

1 Usar algebra de matrices para reescribir la ecuación.
Primero hay que despejar  de la ecuación, por lo que hacemos:
de la ecuación, por lo que hacemos:
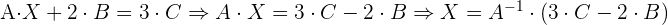
2 Encontrar la matriz inversa de  .
.
Primero revisaremos que  sea invertible, por lo que necesitamos calcular el determinante que es:
sea invertible, por lo que necesitamos calcular el determinante que es:
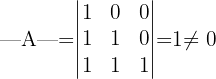
Esto nos dice que la matriz  es invertible.
es invertible.
La matriz inversa de  esta dada por:
esta dada por:
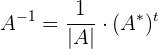
donde

Por lo que haciendo los cálculos obtenemos:

3 Sustituir los valores obtenidos y resolver la ecuación.
Si sustituimos los valores de  ,
,  y
y  en la ecuación y desarrollamos obtenemos:
en la ecuación y desarrollamos obtenemos:
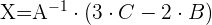

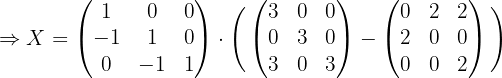


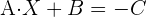
1 Usar algebra de matrices para reescribir la ecuación.
Primero hay que despejar  de la ecuación, por lo que hacemos:
de la ecuación, por lo que hacemos:

2 Sustituir los valores obtenidos y resolver la ecuación.
Si sustituimos los valores de  ,
,  y
y  en la ecuación y desarrollamos obtenemos:
en la ecuación y desarrollamos obtenemos:
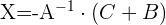
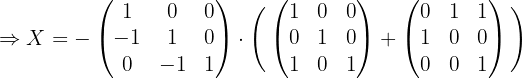
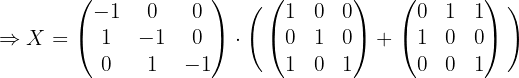
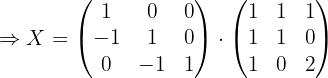
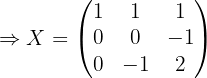
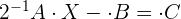
1 Usar algebra de matrices para reescribir la ecuación.
Primero hay que despejar  de la ecuación, por lo que hacemos:
de la ecuación, por lo que hacemos:

2 Sustituir los valores obtenidos y resolver la ecuación.
Si sustituimos los valores de  ,
,  y
y  en la ecuación y desarrollamos obtenemos:
en la ecuación y desarrollamos obtenemos:
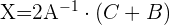


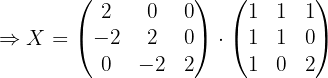
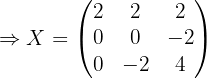
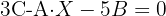
1 Usar algebra de matrices para reescribir la ecuación.
Primero hay que despejar  de la ecuación, por lo que hacemos:
de la ecuación, por lo que hacemos:
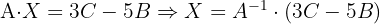
2 Sustituir los valores obtenidos y resolver la ecuación.
Si sustituimos los valores de  ,
,  y
y  en la ecuación y desarrollamos obtenemos:
en la ecuación y desarrollamos obtenemos:
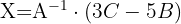
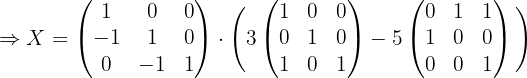

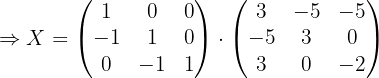
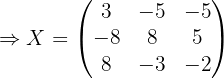

1 Usar algebra de matrices para reescribir la ecuación.
Primero hay que despejar  de la ecuación, por lo que hacemos:
de la ecuación, por lo que hacemos:

2 Recordemos que 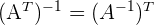 . Sustituir los valores obtenidos y resolver la ecuación.
. Sustituir los valores obtenidos y resolver la ecuación.
Si sustituimos los valores de  ,
,  y
y 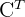 en la ecuación y desarrollamos obtenemos:
en la ecuación y desarrollamos obtenemos:
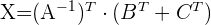


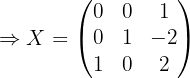
Sistemas de ecuaciones con matrices
Resolver; en forma matricial, el sistema:
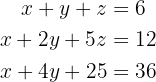
1 Reescribir el sistema de ecuaciones en forma matricial.Con los coeficientes de las ecuaciones podemos formar siguiente matriz:

Ahora tomamos las 3 incógnitas 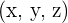 y formamos el vector columna:
y formamos el vector columna:

Por ultimo usamos las soluciones de las ecuaciones y las acomodamos en un vector columna de la siguiente manera:

Por lo que si reescribimos las ecuaciones de forma matricial tenemos:
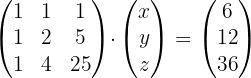


2 Encontrar la inversa de  .
.
Primero revisaremos que  sea invertible, por lo que necesitamos calcular el determinante que es:
sea invertible, por lo que necesitamos calcular el determinante que es:
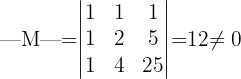
Esto nos dice que la matriz  es invertible.
es invertible.
La matriz inversa de  esta dada por:
esta dada por:

donde

Por lo que haciendo los cálculos obtenemos:
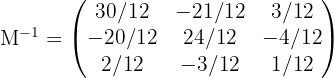
3 Sustituir los valores encontrados y resolver la ecuación.
Tenemos la ecuación:
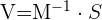
Sí sustituimos los valores de 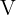 ,
, 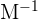 y
y  , y desarrollamos la ecuación tenemos:
, y desarrollamos la ecuación tenemos:

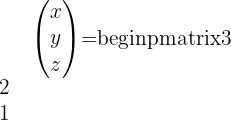
Esto implica que:
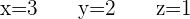
Resolver; en forma matricial, el sistema:
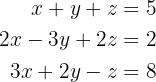
1 Reescribir el sistema de ecuaciones en forma matricial. Con los coeficientes de las ecuaciones podemos formar siguiente matriz:
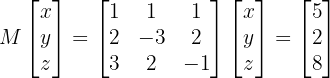
2 Encontrar la inversa de  .Primero revisaremos que
.Primero revisaremos que  sea invertible, por lo que necesitamos calcular el determinante que es:
sea invertible, por lo que necesitamos calcular el determinante que es:
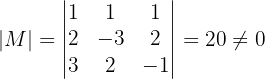
Esto nos dice que la matriz  es invertible.
es invertible.
La matriz inversa de  esta dada por:
esta dada por:
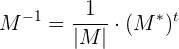
donde

Por lo que haciendo los cálculos obtenemos:
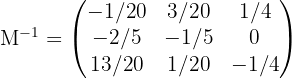
3 Sustituir los valores encontrados y resolver la ecuación.
Tenemos la ecuación:


Esto implica que:

3Resolver; en forma matricial, el sistema:
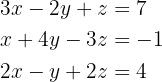
1 Reescribir el sistema de ecuaciones en forma matricial. Con los coeficientes de las ecuaciones podemos formar siguiente matriz:

2 Encontrar la inversa de  .Primero revisaremos que
.Primero revisaremos que  sea invertible, por lo que necesitamos calcular el determinante que es:
sea invertible, por lo que necesitamos calcular el determinante que es:
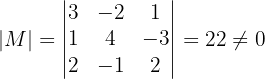
Esto nos dice que la matriz  es invertible.
es invertible.
La matriz inversa de  esta dada por:
esta dada por:
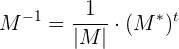
donde

Por lo que haciendo los cálculos obtenemos:
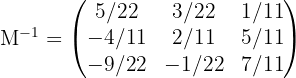
3 Sustituir los valores encontrados y resolver la ecuación.
Tenemos la ecuación:
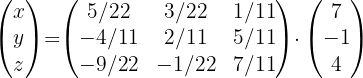
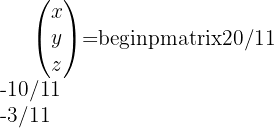
Esto implica que:

Resolver; en forma matricial, el sistema:

1 Reescribir el sistema de ecuaciones en forma matricial. Con los coeficientes de las ecuaciones podemos formar siguiente matriz:

2 Encontrar la inversa de  .Primero revisaremos que
.Primero revisaremos que  sea invertible, por lo que necesitamos calcular el determinante que es:
sea invertible, por lo que necesitamos calcular el determinante que es:
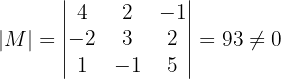
Esto nos dice que la matriz  es invertible.
es invertible.
La matriz inversa de  esta dada por:
esta dada por:
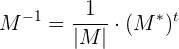
donde

Por lo que haciendo los cálculos obtenemos:

3 Sustituir los valores encontrados y resolver la ecuación.
Tenemos la ecuación:
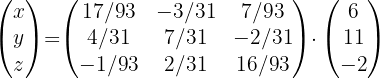
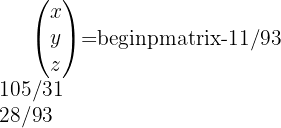
Esto implica que:

Resolver; en forma matricial, el sistema:
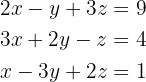
1 Reescribir el sistema de ecuaciones en forma matricial. Con los coeficientes de las ecuaciones podemos formar siguiente matriz:

2 Encontrar la inversa de  .Primero revisaremos que
.Primero revisaremos que  sea invertible, por lo que necesitamos calcular el determinante que es:
sea invertible, por lo que necesitamos calcular el determinante que es:
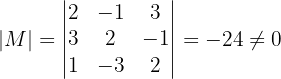
Esto nos dice que la matriz  es invertible.
es invertible.
La matriz inversa de  esta dada por:
esta dada por:
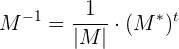
donde

Por lo que haciendo los cálculos obtenemos:

3 Sustituir los valores encontrados y resolver la ecuación.
Tenemos la ecuación:
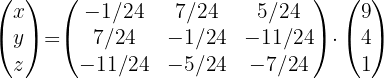

Esto implica que:
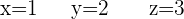
Calculo de Matriz en sistema de ecuaciones
Obtener las matrices A y B que verifiquen el sistema:

Multiplicamos la segunda ecuación por 
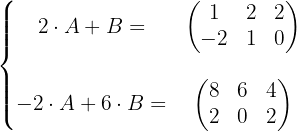
Sumamos le sumamos la segunda ecuación a la primera, por lo que tenemos:
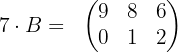
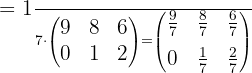
Ahora tomamos la primera ecuación y despejamos para  , sustituyendo el valor encontrado de
, sustituyendo el valor encontrado de 
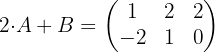
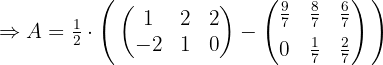

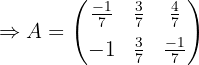
Resolver la ecuación:

Sin desarrollar los determinantes.
Para resolver está ecuación sin hacer el calculo de los determinantes recordemos que el determinante es 0 cuando la matriz no tiene rango completo. Esto es equivalente a que alguna de las filas sea combinación lineal de las otras dos.Denotemos como  a la primera fila,
a la primera fila,  a la segunda fila y
a la segunda fila y  a la tercera fila. Entonces, el determinante será 0 si se cumple:
a la tercera fila. Entonces, el determinante será 0 si se cumple: 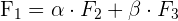
Por lo tanto, con esto podemos formar el siguiente sistema de ecuaciones:
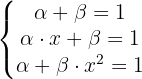
Notemos que, aunque es un sistema no lineal, se tienen 3 variables y tres ecuaciones. Entonces es posible que la podamos resolver. Empezamos igualando las primeras dos ecuaciones:

Aquí hay dos casos, que 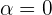 o que
o que  . Si
. Si  , entonces podemos dividir la ecuación por
, entonces podemos dividir la ecuación por  para tener que
para tener que  .
.
Supongamos ahora que 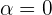 , de la primera ecuación se sigue que:
, de la primera ecuación se sigue que:

por lo tanto, 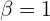 . Luego, en la tercera ecuación tenemos:
. Luego, en la tercera ecuación tenemos:
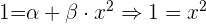
e donde se sigue que  .
.
Por lo tanto, las soluciones son  y
y  .
.
Resolver la ecuación:
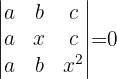
Sin desarrollar los determinantes.
El determinante de este ejercicio es más complicado que el del ejercicio anterior debido a que tenemos entradas arbitrarias  ,
,  y
y  .
.
Sin embargo, si deseamos encontrar todas las soluciones, debemos proceder como en el ejercicio anterior. Primero, denotamos las filas como  ,
,  y
y  . Así, tenemos el siguiente sistema de ecuaciones:
. Así, tenemos el siguiente sistema de ecuaciones:
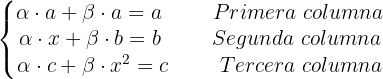
Observemos que las variables de este sistema de ecuaciones son  ,
,  y
y  . Las letras
. Las letras  ,
,  y
y  no son variables, por lo que las soluciones deben estar en términos de
no son variables, por lo que las soluciones deben estar en términos de  ,
,  y
y  .De nuevo tenemos un sistema no lineal. Aquí empezamos despejando
.De nuevo tenemos un sistema no lineal. Aquí empezamos despejando  de la primera ecuación, lo que nos da:
de la primera ecuación, lo que nos da:
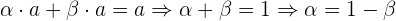
en este caso asumimos que 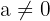 (en el caso de
(en el caso de 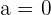 , cualquier valor de
, cualquier valor de  resuelve la ecuación).
resuelve la ecuación).
Si sustituimos el valor de  en la segunda ecuación y despejamos
en la segunda ecuación y despejamos  , obtenemos:
, obtenemos:
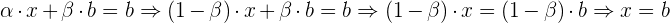
Con esto ultimo ya resolvemos que una solución es  .
.
Ahora, si en lugar de sustituir el valor de 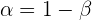 en la segunda ecuación, lo hacemos en la tercera tenemos que:
en la segunda ecuación, lo hacemos en la tercera tenemos que:

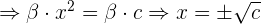
Por lo que tenemos que las soluciones de son:  y
y  .
.
Resolver la ecuación:
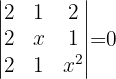
Sin desarrollar los determinantes.
Como ya ha sido mencionado en los ejercicio anteriores, la determinante es cero si una fila o columna es una combinación lineal de las otras filas o columnas, respectivamente. Entonces, tenemos que para algunas constantes 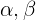 se cumple\begin{bmatrix} 2\\ 2\\ 2 \end{bmatrix} = \alpha\begin{bmatrix} 1\\ x\\ 1 \end{bmatrix} + \beta\begin{bmatrix} 2\\ 1\\ x^2 \end{bmatrix}.
se cumple\begin{bmatrix} 2\\ 2\\ 2 \end{bmatrix} = \alpha\begin{bmatrix} 1\\ x\\ 1 \end{bmatrix} + \beta\begin{bmatrix} 2\\ 1\\ x^2 \end{bmatrix}.
Que es equivalente al sistema de ecuaciones

Entonces, de la primer ecuación tenemos que 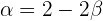 , por lo que obtenemos
, por lo que obtenemos
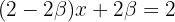
por lo que  . Si usamos
. Si usamos  , obtenemos
, obtenemos
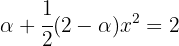
que nos dice que  .
.
Resolver la ecuación:
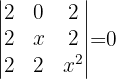
Sin desarrollar los determinantes.
Como ya ha sido mencionado en los ejercicio anteriores, la determinante es cero si una fila o columna es una combinación lineal de las otras filas o columnas, respectivamente. Entonces, tenemos que para algunas constantes 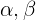 se cumple\begin{bmatrix} 2\\ 2\\ 2 \end{bmatrix} = \alpha\begin{bmatrix} 0\\ x\\ 2 \end{bmatrix} + \beta\begin{bmatrix} 2\\ 2\\ x^2 \end{bmatrix}.
se cumple\begin{bmatrix} 2\\ 2\\ 2 \end{bmatrix} = \alpha\begin{bmatrix} 0\\ x\\ 2 \end{bmatrix} + \beta\begin{bmatrix} 2\\ 2\\ x^2 \end{bmatrix}.
Que es equivalente al sistema de ecuaciones

Entonces, de la primer ecuación tenemos que 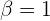 , por lo que obtenemos
, por lo que obtenemos
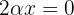
por lo que 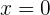 cuando
cuando  . Si
. Si 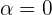 , obtenemos
, obtenemos  .
.
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
En el ejercicio 4 de ecuaciones matriciales se confunden y ponen la matriz C en el lugar de la B y viceversa, pensaba que era error mio de calculo pero creo que esta mal la solucion de ustedes, por el resto me ayudo mucho
Hola revise lo que mencionaste, si había un error pero ya se corrigió, lo que mencionas no lo encontré, podrías revisar y mencionarlo por favor.
Hola, una disculpa por el error, ya se corrigió.
Un número real por una matriz creo que no es el número real por cada elemento de una matriz, sino por los elementos de una sola fila o columna, esto en lo cierto?
Hola el algebra matricial es muy amplia en conceptos, pero lo principal es que una matriz representa arreglos que superan a un solo número real, es como un universo mas amplio que la idea de un solo número real, si no fui claro por favor indícamelo para mejorar.
Muchas gracias , me ayudan mucho con mi examen, solo tenia una duda, en el ejercicio 2 de Sistemas de ecuaciones con matrices, me sale que Y= 8/5, no se en que estoy fallando o creo que se confundieron de símbolo en el elemento de la fila 2 columna 1 de la matriz inversa , debería ser 2/5 y no -2/5.
Hola tienes toda la razón, una disculpa ya se corrigió el error.
Hola, gracias por esto, bien explicado. Por favor, me gustaría también ―pues vengo de las Humanidades― una historia de las matrices. Cómo se inventaron, por quién ; qué necesidad resolvían y no estaba bien cubierta antes. He leído que fueron importantes en aeronáutica. Enhorabuena. ¡Gracias!
Lo tendremos en consideración para nuestro blog 😊 Gracias por tu aporte. Un saludo.
Como resolver 1/2 AB EN MATRICES