Una distribución bidimensional es aquella en las que a cada individuo le corresponden los valores de dos variables, las representamos por el par (xi, yi).
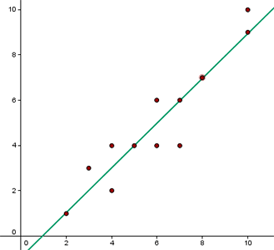
Si representamos cada par de valores como las coordenadas de un punto, el conjunto de todos ellos se llama nube de puntos o diagrama de dispersión.
Sobre la nube de puntos puede trazarse una recta que se ajuste a ellos lo mejor posible, llamada recta de regresión.
Ejemplo
Las notas de 12 alumnos de una clase en Matemáticas y Física son las siguientes:
| Matemáticas | Física |
|---|---|
| 2 | 1 |
| 3 | 3 |
| 4 | 2 |
| 4 | 4 |
| 5 | 4 |
| 6 | 4 |
| 6 | 6 |
| 7 | 4 |
| 7 | 6 |
| 8 | 7 |
| 10 | 9 |
| 10 | 10 |
Covarianza
La covarianza de una variable bidimensional es la media aritmética de los productos de las desviaciones de cada una de las variables respecto a sus medias respectivas.
La covarianza se representa por sxy o σxy.
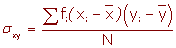

La covarianza indica el sentido de la correlación entre las variables
Si σxy >0 la correlación es directa.
Si σxy <0 la correlación es inversa.
La covarianza presenta como inconveniente, el hecho de que su valor depende de la escala elegida para los ejes.
Es decir, la covarianza variará si expresamos la altura en metros o en centímetros. También variará si el dinero lo expresamos en euros o en dólares.
Correlación
La correlación determina la relación o dependencia que existe entre las dos variables que intervienen en una distribución bidimensional.
Es decir, determinar si los cambios en una de las variables influyen en los cambios de la otra. En caso de que suceda, diremos que las variables están correlacionadas o que hay correlación entre ellas.
Coeficiente de correlación
El coeficiente de correlación lineal se expresa mediante la letra r.

Propiedades
1.
El coeficiente de correlación no varía al hacerlo la escala de medición.Es decir, si expresamos la altura en metros o en centímetros el coeficiente de correlación no varía.
2.
El signo del coeficiente de correlación es el mismo que el de la covarianza.Si la covarianza es positiva, la correlación es directa.
Si la covarianza es negativa, la correlación es inversa.
Si la covarianza es nula, no existe correlación.
3.
El coeficiente de correlación lineal es un número real comprendido entre menos −1 y 1.−1 ≤ r ≤ 1
4.
Si el coeficiente de correlación lineal toma valores cercanos a −1 la correlación es fuerte e inversa, y será tanto más fuerte cuanto más se aproxime r a −1.5.
Si el coeficiente de correlación lineal toma valores cercanos a 1 la correlación es fuerte y directa, y será tanto más fuerte cuanto más se aproxime r a 1.6.
Si el coeficiente de correlación lineal toma valores cercanos a 0, la correlación es débil.7.
Si r = 1 ó −1, los puntos de la nube están sobre la recta creciente o decreciente. Entre ambas variables hay dependencia funcional.Diagramas de dispersión
1º
Correlación directaLa recta correspondiente a la nube de puntos de la distribución es una recta creciente.
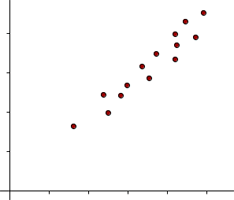
2º
Correlación inversaLa recta correspondiente a la nube de puntos de la distribución es una recta decreciente.
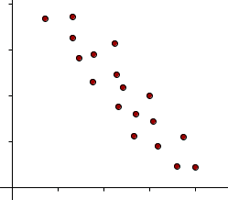
3º
Correlación nulaEn este caso se dice que las variables son incorreladas y la nube de puntos tiene una forma redondeada.

Grado de correlación
El grado de correlación indica la proximidad que hay entre los puntos de la nube de puntos. Se pueden dar tres tipos:
1.
Correlación fuerteLa correlación será fuerte cuanto más cerca estén los puntos de la recta.

2.
Correlación débilLa correlación será débil cuanto más separados estén los puntos de la recta.

3.
Correlación nulaRecta de regresión de Y sobre X
La recta de regresión de Y sobre X se utiliza para estimar los valores de la Y a partir de los de la X.
La pendiente de la recta es el cociente entre la covarianza y la varianza de la variable X.
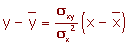
La recta de regresión pasa por el punto 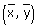
Recta de regresión de X sobre Y
La recta de regresión de X sobre Y se utiliza para estimar los valores de la X a partir de los de la Y.
La pendiente de la recta es el cociente entre la covarianza y la varianza de la variable Y.
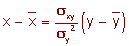
Si la correlación es nula, r = 0, las rectas de regresión son perpendiculares entre sí, y sus eucaciones son:
y = 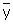
x = 

