En este artículo veremos ejercicios en los cuales elaboraremos la tabla de frecuencias para un conjunto de datos dado.
Durante el mes de julio, en una ciudad se han registrado las siguientes temperaturas máximas:

Crea la tabla de frecuencias, esta debe tener cada dato, sus frecuencias absolutas, frecuencias acumuladas, frecuencias relativas y frecuencias relativas acumuladas.
Notemos que se tienen las siguientes características
1 En la primera columna de la tabla colocamos la variable ordenada de menor a mayor.
2 En la segunda anotamos la frecuencia absoluta (cuándas veces aparece cada dato en específico),  .
.
3 En la tercera anotamos la frecuencia acumulada (La suma de las frecuencias absolutas de la variable actual y las anteriores),  .
.
4 En la primera fila tenemos que la frecuencia absoluta y la acumulada que son iguales: 
5 Para todas las filas que no sean la primera, tenemos que la frecuencia acumulada es igual a la frecuencia absoluta de esta fila más la frecuencia acumulada de la fila anterior, así 
6 La última frecuencia acumulada tiene que ser igual a  (sumatoria de
(sumatoria de  ), esto es,
), esto es,  .
.
7 En la cuarta columna disponemos las frecuencias relativas,  que son el resultado de dividir cada frecuencia absoluta por el total de datos,
que son el resultado de dividir cada frecuencia absoluta por el total de datos,  .
.
8 En la quinta anotamos la frecuencia relativa acumulada  .
.
9 En la primera fila tenemos que la frecuencia relativa acumulada y la frecuencua relativa son iguales: 
10 Para todas las filas que no sean la primera, tenemos que la frecuencia relativa acumulada es igual a la frecuencia relativa de esta fila más la frecuencia relativa acumulada de la fila anterior, así 
Dicho todo lo anterior, la tabla de frecuencias está dada por
 |  |  |  |  |
|---|---|---|---|---|
 |  |  |  |  |
 |  |  | 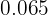 |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |
Durante el invierno, en una ciudad se han registrado las siguientes temperaturas mánimas:

Crea la tabla de frecuencias, esta debe tener cada dato, sus frecuencias absolutas, frecuencias acumuladas, frecuencias relativas y frecuencias relativas acumuladas.
Notemos que se tienen las siguientes características
1 En la primera columna de la tabla colocamos la variable ordenada de menor a mayor.
2 En la segunda anotamos la frecuencia absoluta (cuándas veces aparece cada dato en específico),  .
.
3 En la tercera anotamos la frecuencia acumulada (La suma de las frecuencias absolutas de la variable actual y las anteriores),  .
.
4 En la primera fila tenemos que la frecuencia absoluta y la acumulada que son iguales: 
5 Para todas las filas que no sean la primera, tenemos que la frecuencia acumulada es igual a la frecuencia absoluta de esta fila más la frecuencia acumulada de la fila anterior, así 
6 La última frecuencia acumulada tiene que ser igual a  (sumatoria de
(sumatoria de  ), esto es,
), esto es,  .
.
7 En la cuarta columna disponemos las frecuencias relativas,  que son el resultado de dividir cada frecuencia absoluta por el total de datos,
que son el resultado de dividir cada frecuencia absoluta por el total de datos,  .
.
8 En la quinta anotamos la frecuencia relativa acumulada  .
.
9 En la primera fila tenemos que la frecuencia relativa acumulada y la frecuencua relativa son iguales: 
10 Para todas las filas que no sean la primera, tenemos que la frecuencia relativa acumulada es igual a la frecuencia relativa de esta fila más la frecuencia relativa acumulada de la fila anterior, así 
Dicho todo lo anterior, la tabla de frecuencias está dada por
 |  |  |  |  |
|---|---|---|---|---|
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |
Un trader obtuvo los siguientes precios de cierre por intervalos de un minuto para una criptomoneda:

Crea la tabla de frecuencias, esta debe tener cada dato, sus frecuencias absolutas, frecuencias acumuladas, frecuencias relativas y frecuencias relativas acumuladas.
Notemos que se tienen las siguientes características
1 En la primera columna de la tabla colocamos la variable ordenada de menor a mayor.
2 En la segunda anotamos la frecuencia absoluta (cuándas veces aparece cada dato en específico),  .
.
3 En la tercera anotamos la frecuencia acumulada (La suma de las frecuencias absolutas de la variable actual y las anteriores),  .
.
4 En la primera fila tenemos que la frecuencia absoluta y la acumulada que son iguales: 
5 Para todas las filas que no sean la primera, tenemos que la frecuencia acumulada es igual a la frecuencia absoluta de esta fila más la frecuencia acumulada de la fila anterior, así 
6 La última frecuencia acumulada tiene que ser igual a  (sumatoria de
(sumatoria de  ), esto es,
), esto es,  .
.
7 En la cuarta columna disponemos las frecuencias relativas,  que son el resultado de dividir cada frecuencia absoluta por el total de datos,
que son el resultado de dividir cada frecuencia absoluta por el total de datos,  .
.
8 En la quinta anotamos la frecuencia relativa acumulada  .
.
9 En la primera fila tenemos que la frecuencia relativa acumulada y la frecuencua relativa son iguales: 
10 Para todas las filas que no sean la primera, tenemos que la frecuencia relativa acumulada es igual a la frecuencia relativa de esta fila más la frecuencia relativa acumulada de la fila anterior, así 
Dicho todo lo anterior, la tabla de frecuencias está dada por
 |  |  |  |  |
|---|---|---|---|---|
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |
El número de horas de estudio de un grupo de estudiantes previo a un examen de matemáticas son:

Crea la tabla de frecuencias, esta debe tener cada dato, sus frecuencias absolutas, frecuencias acumuladas, frecuencias relativas y frecuencias relativas acumuladas.
Notemos que se tienen las siguientes características
1 En la primera columna de la tabla colocamos la variable ordenada de menor a mayor.
2 En la segunda anotamos la frecuencia absoluta (cuándas veces aparece cada dato en específico),  .
.
3 En la tercera anotamos la frecuencia acumulada (La suma de las frecuencias absolutas de la variable actual y las anteriores),  .
.
4 En la primera fila tenemos que la frecuencia absoluta y la acumulada que son iguales: 
5 Para todas las filas que no sean la primera, tenemos que la frecuencia acumulada es igual a la frecuencia absoluta de esta fila más la frecuencia acumulada de la fila anterior, así 
6 La última frecuencia acumulada tiene que ser igual a  (sumatoria de
(sumatoria de  ), esto es,
), esto es,  .
.
7 En la cuarta columna disponemos las frecuencias relativas,  que son el resultado de dividir cada frecuencia absoluta por el total de datos,
que son el resultado de dividir cada frecuencia absoluta por el total de datos,  .
.
8 En la quinta anotamos la frecuencia relativa acumulada  .
.
9 En la primera fila tenemos que la frecuencia relativa acumulada y la frecuencua relativa son iguales: 
10 Para todas las filas que no sean la primera, tenemos que la frecuencia relativa acumulada es igual a la frecuencia relativa de esta fila más la frecuencia relativa acumulada de la fila anterior, así 
Dicho todo lo anterior, la tabla de frecuencias está dada por
 |  |  |  |  |
|---|---|---|---|---|
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |
Los pesos en kilogramos de un grupo de personas es:

Crea la tabla de frecuencias, esta debe tener cada dato, sus frecuencias absolutas, frecuencias acumuladas, frecuencias relativas y frecuencias relativas acumuladas.
Notemos que se tienen las siguientes características
1 En la primera columna de la tabla colocamos la variable ordenada de menor a mayor.
2 En la segunda anotamos la frecuencia absoluta (cuándas veces aparece cada dato en específico),  .
.
3 En la tercera anotamos la frecuencia acumulada (La suma de las frecuencias absolutas de la variable actual y las anteriores),  .
.
4 En la primera fila tenemos que la frecuencia absoluta y la acumulada que son iguales: 
5 Para todas las filas que no sean la primera, tenemos que la frecuencia acumulada es igual a la frecuencia absoluta de esta fila más la frecuencia acumulada de la fila anterior, así 
6 La última frecuencia acumulada tiene que ser igual a  (sumatoria de
(sumatoria de  ), esto es,
), esto es,  .
.
7 En la cuarta columna disponemos las frecuencias relativas,  que son el resultado de dividir cada frecuencia absoluta por el total de datos,
que son el resultado de dividir cada frecuencia absoluta por el total de datos,  .
.
8 En la quinta anotamos la frecuencia relativa acumulada  .
.
9 En la primera fila tenemos que la frecuencia relativa acumulada y la frecuencua relativa son iguales: 
10 Para todas las filas que no sean la primera, tenemos que la frecuencia relativa acumulada es igual a la frecuencia relativa de esta fila más la frecuencia relativa acumulada de la fila anterior, así 
Dicho todo lo anterior, la tabla de frecuencias está dada por
 |  |  |  |  |
|---|---|---|---|---|
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |
Los pesos de los  empleados de una fábrica vienen dados por la siguiente tabla
empleados de una fábrica vienen dados por la siguiente tabla
| Peso |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
Crear su respectiva tabla de frecuencias.
Notemos que la tabla de frecuencias debe cumplir lo siguiente
1 En la primera columna de la tabla colocamos los intervalos o grupos. Ya tenemos esta columna.
2 En la segunda anotamos la frecuencia absoluta (cuándas veces aparece cada dato en específico),  . Ya tenemos esta columna.
. Ya tenemos esta columna.
3 En la tercera anotamos la frecuencia acumulada (La suma de las frecuencias absolutas de la variable actual y las anteriores),  .
.
4 En la primera fila tenemos que la frecuencia absoluta y la acumulada que son iguales: 
5 Para todas las filas que no sean la primera, tenemos que la frecuencia acumulada es igual a la frecuencia absoluta de esta fila más la frecuencia acumulada de la fila anterior, así 
6 La última frecuencia acumulada tiene que ser igual a  (sumatoria de
(sumatoria de  ), esto es,
), esto es,  .
.
7 En la cuarta columna disponemos las frecuencias relativas,  que son el resultado de dividir cada frecuencia absoluta por el total de datos,
que son el resultado de dividir cada frecuencia absoluta por el total de datos,  .
.
8 En la quinta anotamos la frecuencia relativa acumulada  .
.
9 En la primera fila tenemos que la frecuencia relativa acumulada y la frecuencua relativa son iguales: 
10 Para todas las filas que no sean la primera, tenemos que la frecuencia relativa acumulada es igual a la frecuencia relativa de esta fila más la frecuencia relativa acumulada de la fila anterior, así 
Dicho todo lo anterior, la tabla está dada por
 |  |  |  |  | |
 |  |  |  |  |  |
 |  |  |  |  | 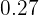 |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |
Las alturas de  alumnos vienen dados por la siguiente tabla
alumnos vienen dados por la siguiente tabla
| Altura |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
Crear su respectiva tabla de frecuencias.
Notemos que la tabla de frecuencias debe cumplir lo siguiente
1 En la primera columna de la tabla colocamos los intervalos o grupos. Ya tenemos esta columna.
2 En la segunda anotamos la frecuencia absoluta (cuándas veces aparece cada dato en específico),  . Ya tenemos esta columna.
. Ya tenemos esta columna.
3 En la tercera anotamos la frecuencia acumulada (La suma de las frecuencias absolutas de la variable actual y las anteriores),  .
.
4 En la primera fila tenemos que la frecuencia absoluta y la acumulada que son iguales: 
5 Para todas las filas que no sean la primera, tenemos que la frecuencia acumulada es igual a la frecuencia absoluta de esta fila más la frecuencia acumulada de la fila anterior, así 
6 La última frecuencia acumulada tiene que ser igual a  (sumatoria de
(sumatoria de  ), esto es,
), esto es,  .
.
7 En la cuarta columna disponemos las frecuencias relativas,  que son el resultado de dividir cada frecuencia absoluta por el total de datos,
que son el resultado de dividir cada frecuencia absoluta por el total de datos,  .
.
8 En la quinta anotamos la frecuencia relativa acumulada  .
.
9 En la primera fila tenemos que la frecuencia relativa acumulada y la frecuencua relativa son iguales: 
10 Para todas las filas que no sean la primera, tenemos que la frecuencia relativa acumulada es igual a la frecuencia relativa de esta fila más la frecuencia relativa acumulada de la fila anterior, así 
Dicho todo lo anterior, la tabla está dada por
 |  |  |  |  |
|---|---|---|---|---|
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |
Un profesor observa las calificaciones de los  niños de cierto colegio. La información obtenida a parecer resumida en la siguiente tabla:
niños de cierto colegio. La información obtenida a parecer resumida en la siguiente tabla:
| Calificación |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
Completar la tabla obteniendo los valores  .
.
Tenemos que siempre la suma de todas las frecuencias relativas es igual a  . Esto quiere decir que
. Esto quiere decir que

Por lo tanto  . Ahora, tenemos que
. Ahora, tenemos que  es la frecuencia relativa del grupo con calificación
es la frecuencia relativa del grupo con calificación  , mientras que la frecuencia absoluta es
, mientras que la frecuencia absoluta es  . Además, notemos que
. Además, notemos que  ya que son datos de
ya que son datos de  niños. Así, tenemos que la frecuencia relativa es la frecuencia absoluta entre
niños. Así, tenemos que la frecuencia relativa es la frecuencia absoluta entre  , usaremos este hecho para encontrar
, usaremos este hecho para encontrar 

Ahora ya tenemos los datos necesarios para completar nuestra tabla
| Calificación |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |
Un dentista observa el número de caries en cada uno de los  niños de cierto colegio. La información obtenida a parecer resumida en la siguiente tabla:
niños de cierto colegio. La información obtenida a parecer resumida en la siguiente tabla:
| Número de caries |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
Completar la tabla obteniendo los valores  .
.
Tenemos que siempre la suma de todas las frecuencias relativas es igual a  . Esto quiere decir que
. Esto quiere decir que

Por lo tanto  . Ahora, tenemos que
. Ahora, tenemos que  es la frecuencia relativa del grupo con
es la frecuencia relativa del grupo con  caries, mientras que la frecuencia absoluta es
caries, mientras que la frecuencia absoluta es  . Además, notemos que
. Además, notemos que  ya que son datos de
ya que son datos de  niños. Así, tenemos que la frecuencia relativa es la frecuencia absoluta entre
niños. Así, tenemos que la frecuencia relativa es la frecuencia absoluta entre  , usaremos este hecho para encontrar
, usaremos este hecho para encontrar 

Solo nos falta encontrar  que es la frecuencia absoluta del grupo con
que es la frecuencia absoluta del grupo con  caries, mientras que su frecuencia relativa es
caries, mientras que su frecuencia relativa es  . Tenemos que la frecuencia relativa es la frecuencia absoluta entre
. Tenemos que la frecuencia relativa es la frecuencia absoluta entre  , usaremos este hecho para encontrar
, usaremos este hecho para encontrar 

Ahora ya tenemos los datos necesarios para completar nuestra tabla
| Número de caries |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |
Completar los datos que faltan en la siguiente tabla estadística:
 |  |  |  |
 |  |  | |
 |  | ||
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  | |
 |  |  |
Resolveremos esto paso por paso, primero encontraremos el valor de  y posteriormente encontraremos todos los datos faltantes de cada fila.
y posteriormente encontraremos todos los datos faltantes de cada fila.
1 Encontramos el valor de  , el cual se obtiene de la última fila de la frecuencia acumulada.
, el cual se obtiene de la última fila de la frecuencia acumulada.
2 Primer fila. Es sencillo, solo nos falta la frecuencia acumulada,  , pero al ser la primer fila (primer clase), esta es igual a la frecuencia absoluta, por lo tanto,
, pero al ser la primer fila (primer clase), esta es igual a la frecuencia absoluta, por lo tanto,

3 Segunda Fila. Primero encontremos la frecuencia acumulada, recordemos que esta es igual a

Ahora encontremos la frecuencia relativa, dado que ya tenemos la frecuencia absoluta tenemos que

4 Séptima fila. Únicamente nos falta la frecuencia absoluta, esta la podemos obtener a través de la frecuencia acumulada o la frecuencia relativa, nosotros procedemos a traves de la frecuencia acumulada

5 Octava fila. Únicamente nos falta la frecuencia absoluta, la calcularemos directamente

Así, la tabla está dada por
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |
Completar los datos que faltan en la siguiente tabla estadística:
 |  |  |  |
 |  |  | |
 |  | ||
 |  |  | |
 |  |  | |
 |  |  | |
 |  | ||
 |  |  | |
 |
Resolveremos esto paso por paso, primero encontraremos el valor de  y posteriormente encontraremos todos los datos faltantes de cada fila.
y posteriormente encontraremos todos los datos faltantes de cada fila.
1 Primero encontremos el valor de  .
.
Para encontrar el valor de  usaremos la primera fila. Recordemos que la frecuencia relativa es la frecuencia absoluta entre
usaremos la primera fila. Recordemos que la frecuencia relativa es la frecuencia absoluta entre  , dado que tenemos la frecuencia absoluta
, dado que tenemos la frecuencia absoluta  y la frecuencia relativa
y la frecuencia relativa  , usaremos esto para despejar
, usaremos esto para despejar 

2 Primer fila. Es sencillo, solo nos falta la frecuencia acumulada,  , pero al ser la primer fila (primer clase), esta es igual a la frecuencia absoluta, por lo tanto,
, pero al ser la primer fila (primer clase), esta es igual a la frecuencia absoluta, por lo tanto,

3 Segunda Fila. Primero encontremos la frecuencia acumulada, recordemos que esta es igual a

Ahora encontremos la frecuencia relativa, dado que ya tenemos la frecuencia absoluta tenemos que

4 Tercer fila. Únicamente nos falta la frecuencia absoluta, esta la podemos obtener a través de la frecuencia acumulada o la frecuencia relativa, nosotros procedemos a traves de la frecuencia acumulada

5 Cuarta fila. Únicamente nos falta la frecuencia acumulada, la calcularemos directamente

6 Quinta fila. Únicamente nos falta la frecuencia relativa, la calcularemos directamente

7 Sexta fila. Nos falta la frecuencia absoluta y la frecuencia relativa. Calculemos la frecuencia absoluta por medio de la frecuencia absoluta.

Ahora calculemos la frecuencia relativa directamente usando la frecuencia absoluta

8 Séptima fila. Únicamente lnos falta la frecuencia relativa, la calcularemos directamente

9 Octava y última fila. Nos faltan todos los datos. Primero obtengamos la frecuencia acumulada. Notemos que debido a que es la última fila, la frecuencia acumulada es igual a  , por lo tanto
, por lo tanto

Ahora obtegamos la frecuencia aabsoluta a través de la frecuencia acumulada

Por último obtengamos la frecuencia relativa de forma directa

Así, la tabla está dada por
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |
Durante un campeonato de fútbol que consiste de 38 fechas, un equipo anotó los siguientes goles:

Crea la tabla de frecuencias, esta debe tener cada dato, sus frecuencias absolutas, frecuencias acumuladas, frecuencias relativas y frecuencias relativas acumuladas.
Notemos que se tienen las siguientes características
1 En la primera columna de la tabla colocamos la variable ordenada de menor a mayor.
2 En la segunda anotamos la frecuencia absoluta (cuándas veces aparece cada dato en específico),  .
.
3 En la tercera anotamos la frecuencia acumulada (La suma de las frecuencias absolutas de la variable actual y las anteriores),  .
.
4 En la primera fila tenemos que la frecuencia absoluta y la acumulada que son iguales: 
5 Para todas las filas que no sean la primera, tenemos que la frecuencia acumulada es igual a la frecuencia absoluta de esta fila más la frecuencia acumulada de la fila anterior, así 
6 La última frecuencia acumulada tiene que ser igual a  (sumatoria de
(sumatoria de  ), esto es,
), esto es,  .
.
7 En la cuarta columna disponemos las frecuencias relativas,  que son el resultado de dividir cada frecuencia absoluta por el total de datos,
que son el resultado de dividir cada frecuencia absoluta por el total de datos, 
8 En la quinta anotamos la frecuencia relativa acumulada  .
.
9 En la primera fila tenemos que la frecuencia relativa acumulada y la frecuencua relativa son iguales: 
10 Para todas las filas que no sean la primera, tenemos que la frecuencia relativa acumulada es igual a la frecuencia relativa de esta fila más la frecuencia relativa acumulada de la fila anterior, así
Dicho todo lo anterior, la tabla de frecuencias está dada por
 |  |  |  |  |
|---|---|---|---|---|
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  | 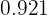 |
 |  |  |  |  |
 |  |  |  |  |
 |  |
La audiencia (en millones de personas) de una serie de televisión durante los  capítulos de su primer temporada vienen dados en la siguiente tabla:
capítulos de su primer temporada vienen dados en la siguiente tabla:
| Peso |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
Crear su respectiva tabla de frecuencias.
Notemos que la tabla de frecuencias debe cumplir lo siguiente
1 En la primera columna de la tabla colocamos los intervalos o grupos. Ya tenemos esta columna.
2 En la segunda anotamos la frecuencia absoluta (cuántas veces aparece cada dato en específico),  . Ya tenemos esta columna.
. Ya tenemos esta columna.
3 En la tercera anotamos la frecuencia acumulada (La suma de las frecuencias absolutas de la variable actual y las anteriores),  .
.
4 En la primera fila tenemos que la frecuencia absoluta y la acumulada que son iguales: 
5 Para todas las filas que no sean la primera, tenemos que la frecuencia acumulada es igual a la frecuencia absoluta de esta fila más la frecuencia acumulada de la fila anterior, así 
6 La última frecuencia acumulada tiene que ser igual a  (sumatoria de
(sumatoria de  ), esto es,
), esto es,  .
.
7 En la cuarta columna disponemos las frecuencias relativas,  , que son el resultado de dividir cada frecuencia absoluta por el total de datos,
, que son el resultado de dividir cada frecuencia absoluta por el total de datos,  .
.
8 En la quinta anotamos la frecuencia relativa acumulada  .
.
9 En la primera fila tenemos que la frecuencia relativa acumulada y la frecuencua relativa son iguales: 
10 Para todas las filas que no sean la primera, tenemos que la frecuencia relativa acumulada es igual a la frecuencia relativa de esta fila más la frecuencia relativa acumulada de la fila anterior, así 
Dicho todo lo anterior, la tabla está dada por
 |  |  |  |  | |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |
Las calificaciones de los  estudiantes que tomaron la clase de matemáticas el año pasado son:
estudiantes que tomaron la clase de matemáticas el año pasado son:

Crea la tabla de frecuencias, esta debe tener cada dato, sus frecuencias absolutas, frecuencias acumuladas, frecuencias relativas y frecuencias relativas acumuladas.
Notemos que se tienen las siguientes características
1 En la primera columna de la tabla colocamos la variable ordenada de menor a mayor.
2 En la segunda anotamos la frecuencia absoluta (cuándas veces aparece cada dato en específico),  .
.
3 En la tercera anotamos la frecuencia acumulada (La suma de las frecuencias absolutas de la variable actual y las anteriores),  .
.
4 En la primera fila tenemos que la frecuencia absoluta y la acumulada que son iguales: 
5 Para todas las filas que no sean la primera, tenemos que la frecuencia acumulada es igual a la frecuencia absoluta de esta fila más la frecuencia acumulada de la fila anterior, así 
6 La última frecuencia acumulada tiene que ser igual a  (sumatoria de
(sumatoria de  ), esto es,
), esto es,  .
.
7 En la cuarta columna disponemos las frecuencias relativas,  que son el resultado de dividir cada frecuencia absoluta por el total de datos,
que son el resultado de dividir cada frecuencia absoluta por el total de datos, 
8 En la quinta anotamos la frecuencia relativa acumulada  .
.
9 En la primera fila tenemos que la frecuencia relativa acumulada y la frecuencua relativa son iguales: 
10 Para todas las filas que no sean la primera, tenemos que la frecuencia relativa acumulada es igual a la frecuencia relativa de esta fila más la frecuencia relativa acumulada de la fila anterior, así
Dicho todo lo anterior, la tabla de frecuencias está dada por
 |  |  |  |  |
|---|---|---|---|---|
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |
En una tienda departamental se registró el número de prendas que cada uno de sus últimos  clientes compró. Esta información se resume en la siguiente tabla:
clientes compró. Esta información se resume en la siguiente tabla:
| Número de prendas |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
Completar la tabla obteniendo los valores  .
.
Tenemos que siempre la suma de todas las frecuencias relativas es igual a  . Esto quiere decir que
. Esto quiere decir que

Por lo tanto  . Ahora, tenemos que
. Ahora, tenemos que  es la frecuencia relativa del grupo que compró
es la frecuencia relativa del grupo que compró  prendas, mientras que la frecuencia absoluta es
prendas, mientras que la frecuencia absoluta es  . Además, notemos que
. Además, notemos que  ya que son datos de
ya que son datos de  clientes. Así, tenemos que la frecuencia relativa es la frecuencia absoluta entre
clientes. Así, tenemos que la frecuencia relativa es la frecuencia absoluta entre  , usaremos este hecho para encontrar
, usaremos este hecho para encontrar 

Solo nos falta encontrar  que es la frecuencia absoluta del grupo que compró
que es la frecuencia absoluta del grupo que compró  prendas, mientras que su frecuencia relativa es
prendas, mientras que su frecuencia relativa es  . Tenemos que la frecuencia relativa es la frecuencia absoluta entre
. Tenemos que la frecuencia relativa es la frecuencia absoluta entre  , usaremos este hecho para encontrar
, usaremos este hecho para encontrar 

Ahora ya tenemos los datos necesarios para completar nuestra tabla
| Número de caries |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
en la realización de esta actividad vimos de manera clara toda la distribución de datos. en actividad de las diagramas de barra identificamos las categorías y los intervalos de mayor a menor frecuencia, ya que en la actividad de los polígonos llevamos acabo las tendencias y variables de todo el conjunto de datos. esto son las herramientas que mas utilizamos para hacer la interpretación de datos con la ayuda de ka estadística y hace la comparación de diversos grupos y variables.
Hola excelente resumen de lo que se analiza en el artículo, te felicitamos.
4. La tabla registra el ahorro mensual de s/. 100 mensuales. Completa la tabla y contesta.
a) ¿Cuál es la suma de la tercera y cuarta frecuencia absoluta acumulada?
b) ¿Cuántos estudiantes tienen ahorros mayores o iguales que S/. 20, pero menores que S/. 40?
c) ¿Qué porcentaje de estudiantes tienen ahorros menores que S/. 30?
d) ¿A qué intervalo pertenecen los ahorros de la mayoría de los estudiantes?
Lo unico que no me parecio del ejercicio es que al momento de redondear por ejemplo cuando el resultados es .155 asi fue como lo escribi pero me lo marcaba incorrecto, ya que pedia redondear a 16%
Entonces eso complico un poco a la hora de los resultados.
Hola entendemos tu frustración, pero como a veces sucede que algunos libros o maestros piden redondear y otros no, entonces se tomo este criterio que es mas generalizado.
Hay varios tipos de gráficos