En esta sección practicaremos un conjunto de ejercicios de varianza. En cada pregunta escoge la respuesta que represente la varianza del conjunto de datos dados.
El número de veces que un grupo de tres amigos, come pasta durante una semana un grupo es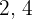 
y 
respectivamente
Selecciona una respuesta.
Primero calculemos el promedio:
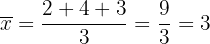
Luego calculemos la varianza:
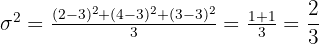
Los litros de agua que beben al día un grupo de cuatro amigos son 
. Entonces la varianza de este conjunto de datos es:
Selecciona una respuesta.
Primero calculemos el promedio:
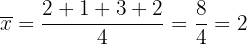
Luego calculemos la varianza:
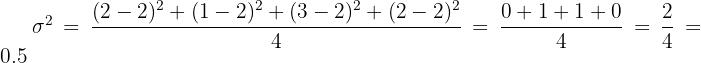
El número de horas que Carmen ha visto la tele durante cada día de la semana pasada es: 
, de este conjunto de datos la varianza es:
Selecciona una respuesta.
Primero calculemos el promedio:
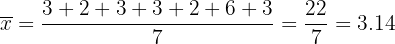
Luego calculemos la varianza:
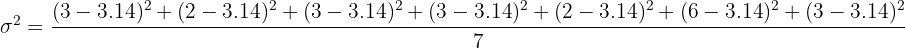
Las veces que se cepilla María los dientes al día durante una semana: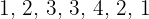 
, entonces la varianza de este conjunto de datos es:
Selecciona una respuesta.
Primero calculemos el promedio:
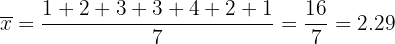
Luego calculemos la varianza:
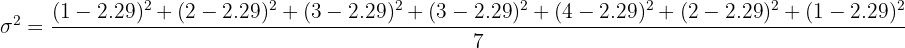
Las notas de los exámenes de matemáticas realizados durante el curso por Pablo son
. De este conjunto de datos la varianza es:
Selecciona una respuesta.
Primero calculemos el promedio:
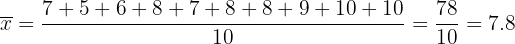
Luego calculemos la varianza:
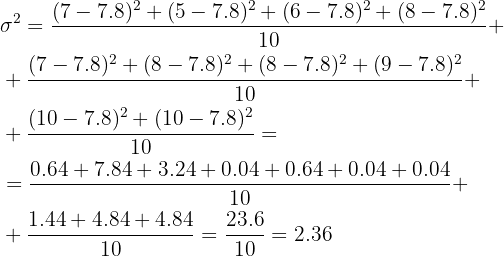
El número de horas que dedican los diez grupos de alumnos formados en una clase al realizar un trabajo de investigación sobre de Geometría es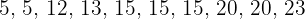 
. La varianza de este conjunto de datos es:
Selecciona una respuesta.
Primero calculemos el promedio:
.
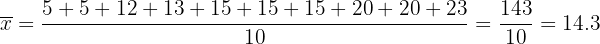Finalmente, calculamos la varianza:
Las estaturas en centímetros de un grupo de cinco amigos es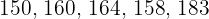 
. La varianza de este conjunto de datos es:
Selecciona una respuesta.
Calculamos el promedio:
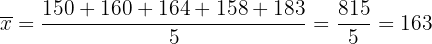
Luego, la varianza:
El número de veces que va al cine en un mes cada componente de un grupo de once amigos es 
. La varianza de este conjunto de datos es:
Selecciona una respuesta.
Al igual que en los ejercicios anteriores primero calculamos el promedio y luego usamos esto para obtener la varianza:
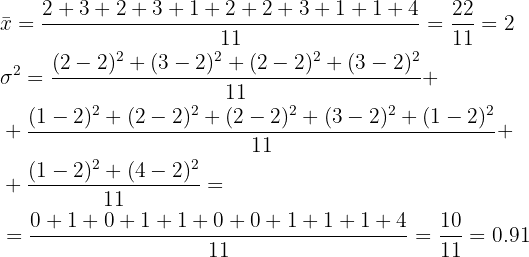
Contesta a las siguientes cuestiones:
Las notas de matemáticas de los 26 alumnos de una clase son 
.
Calcula la varianza de las notas obtenidas, redondeando a dos cifras decimales si fuese necesario:
=
Este campo es obligatorio.
Primero, podemos reescribir los datos considerando los valores (
) y la frecuencia (
) con la que aparecen para después calcular sus productos:
| xi | fi | xi · fi | xi² · fi |
|---|---|---|---|
| 2 | 1 | 2 | 4 |
| 3 | 3 | 9 | 27 |
| 4 | 7 | 28 | 112 |
| 5 | 6 | 30 | 150 |
| 6 | 6 | 36 | 216 |
| 7 | 2 | 14 | 98 |
| 8 | 1 | 8 | 64 |
| Total | 26 | 127 | 671 |
Una vez que conocemos la suma de todos los calculamos el promedio:
.
Finalmente, calculamos la varianza:
.
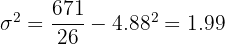Las faltas de asistencia de 25 alumnos de otra clase son: 
. Calcula la varianza:
=
Este campo es obligatorio.
Primero, podemos reescribir los datos en una tabla considerando los valores () y la frecuencia () con la que aparecen para después calcular sus productos:
| xi | fi | xi · fi | xi² · fi |
|---|---|---|---|
| 0 | 6 | 0 | 0 |
| 1 | 8 | 8 | 8 |
| 2 | 6 | 12 | 24 |
| 3 | 1 | 3 | 9 |
| 4 | 1 | 4 | 16 |
| 6 | 1 | 6 | 36 |
| 7 | 2 | 14 | 98 |
| Total | 25 | 47 | 191 |
Una vez que conocemos la suma de todos los y el total de datos calculamos el promedio:
.
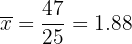Finalmente, calculamos la varianza:
.
Si tienes dudas puedes consultar la teoría
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
en la realización de esta actividad vimos de manera clara toda la distribución de datos. en actividad de las diagramas de barra identificamos las categorías y los intervalos de mayor a menor frecuencia, ya que en la actividad de los polígonos llevamos acabo las tendencias y variables de todo el conjunto de datos. esto son las herramientas que mas utilizamos para hacer la interpretación de datos con la ayuda de ka estadística y hace la comparación de diversos grupos y variables.
Hola excelente resumen de lo que se analiza en el artículo, te felicitamos.
4. La tabla registra el ahorro mensual de s/. 100 mensuales. Completa la tabla y contesta.
a) ¿Cuál es la suma de la tercera y cuarta frecuencia absoluta acumulada?
b) ¿Cuántos estudiantes tienen ahorros mayores o iguales que S/. 20, pero menores que S/. 40?
c) ¿Qué porcentaje de estudiantes tienen ahorros menores que S/. 30?
d) ¿A qué intervalo pertenecen los ahorros de la mayoría de los estudiantes?
Lo unico que no me parecio del ejercicio es que al momento de redondear por ejemplo cuando el resultados es .155 asi fue como lo escribi pero me lo marcaba incorrecto, ya que pedia redondear a 16%
Entonces eso complico un poco a la hora de los resultados.
Hola entendemos tu frustración, pero como a veces sucede que algunos libros o maestros piden redondear y otros no, entonces se tomo este criterio que es mas generalizado.
Hay varios tipos de gráficos