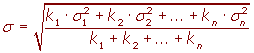Las medidas de dispersión nos informan sobre cuánto se alejan del centro los valores de la distribución.
Las medidas de dispersión son:
Rango o recorrido
El rango es la diferencia entre el mayor y el menor de los datos de una distribución estadística.
Desviación media
La desviación respecto a la media es la diferencia entre cada valor de la variable estadística y la media aritmética.
Di = x - x
La desviación media es la media aritmética de los valores absolutos de las desviaciones respecto a la media.
La desviación media se representa por 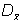

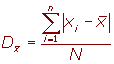
Ejemplo
Calcular la desviación media de la distribución:
9, 3, 8, 8, 9, 8, 9, 18
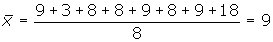
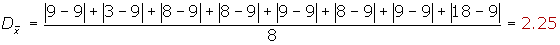
Si los datos vienen agrupados en una tabla de frecuencias, la expresión de la desviación media es:
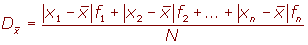
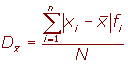
Ejemplo
Calcular la desviación media de la distribución:
| xi | fi | xi · fi | |x - x| | |x - x| · fi | |
| [10, 15) | 12.5 | 3 | 37.5 | 9.286 | 27.858 |
|---|---|---|---|---|---|
| [15, 20) | 17.5 | 5 | 87.5 | 4.286 | 21.43 |
| [20, 25) | 22.5 | 7 | 157.5 | 0.714 | 4.998 |
| [25, 30) | 27.5 | 4 | 110 | 5.714 | 22.856 |
| [30, 35) | 32.5 | 2 | 65 | 10.174 | 21.428 |
| 21 | 457.5 | 98.57 |
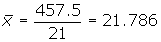
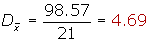
Varianza
La varianza es la media aritmética del cuadrado de las desviaciones respecto a la media de una distribución estadística.
La varianza se representa por 


Varianza para datos agrupados


Para simplificar el cálculo de la varianza vamos o utilizar las siguientes expresiones que son equivalentes a las anteriores.
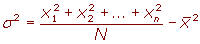
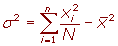
Varianza para datos agrupados

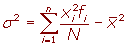
Ejercicios de varianza
Calcular la varianza de la distribución:
9, 3, 8, 8, 9, 8, 9, 18


Calcular la varianza de la distribución de la tabla:
| xi | fi | xi · fi | xi2 · fi | |
|---|---|---|---|---|
| [10, 20) | 15 | 1 | 15 | 225 |
| [20, 30) | 25 | 8 | 200 | 5000 |
| [30,40) | 35 | 10 | 350 | 12 250 |
| [40, 50) | 45 | 9 | 405 | 18 225 |
| [50, 60 | 55 | 8 | 440 | 24 200 |
| [60,70) | 65 | 4 | 260 | 16 900 |
| [70, 80) | 75 | 2 | 150 | 11 250 |
| 42 | 1 820 | 88 050 |
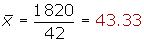

1
La varianza será siempre un valor positivo o cero, en el caso de que las puntuaciones sean iguales.2
Si a todos los valores de la variable se les suma un número la varianza no varía.3
Si todos los valores de la variable se multiplican por un número la varianza queda multiplicada por el cuadrado de dicho número.4
Si tenemos varias distribuciones con la misma media y conocemos sus respectivas varianzas se puede calcular la varianza total.Si todas las muestras tienen el mismo tamaño:

Si las muestras tienen distinto tamaño:
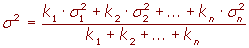
Observaciones sobre la varianza
1
La varianza, al igual que la media, es un índice muy sensible a las puntuaciones extremas.2
En los casos que no se pueda hallar la media tampoco será posible hallar la varianza.3
La varianza no viene expresada en las mismas unidades que los datos, ya que las desviaciones están elevadas al cuadrado.Desviación típica
La desviación típica es la raíz cuadrada de la varianza.
Es decir, la raíz cuadrada de la media de los cuadrados de las puntuaciones de desviación.
La desviación típica se representa por σ.
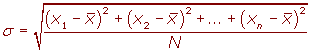
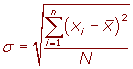
Desviación típica para datos agrupados
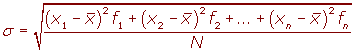
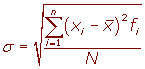
Para simplificar el cálculo vamos o utilizar las siguientes expresiones que son equivalentes a las anteriores.
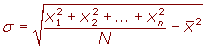
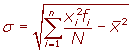
Desviación típica para datos agrupados
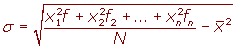
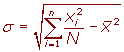
Ejercicios de desviación típica
Calcular la desviación típica de la distribución:
9, 3, 8, 8, 9, 8, 9, 18
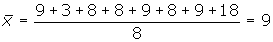
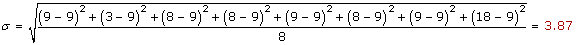
Calcular la desviación típica de la distribución de la tabla:
| xi | fi | xi · fi | xi2 · fi | |
|---|---|---|---|---|
| [10, 20) | 15 | 1 | 15 | 225 |
| [20, 30) | 25 | 8 | 200 | 5000 |
| [30,40) | 35 | 10 | 350 | 12 250 |
| [40, 50) | 45 | 9 | 405 | 18 225 |
| [50, 60) | 55 | 8 | 440 | 24 200 |
| [60,70) | 65 | 4 | 260 | 16 900 |
| [70, 80) | 75 | 2 | 150 | 11 250 |
| 42 | 1 820 | 88 050 |
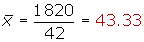
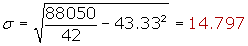
1
La desviación típica será siempre un valor positivo o cero, en el caso de que las puntuaciones sean iguales.2
Si a todos los valores de la variable se les suma un número la desviación típica no varía.3
Si todos los valores de la variable se multiplican por un número la desviación típica queda multiplicada por dicho número.4
Si tenemos varias distribuciones con la misma media y conocemos sus respectivas desviaciones típicas se puede calcular la desviación típica total.Si todas las muestras tienen el mismo tamaño:

Si las muestras tienen distinto tamaño: