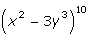La fórmula que nos permite hallar las potencias de un binomio se conoce como binomio de Newton.
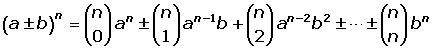
Podemos observar que:
El número de términos es n+1.
Los coeficientes son números combinatorios que corresponden a la fila enésima del triángulo de Tartaglia.
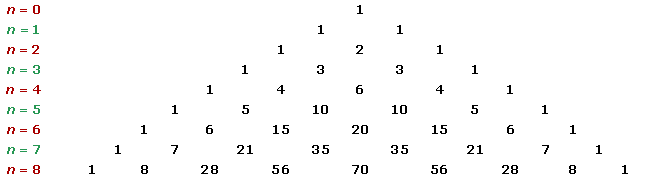
En el desarrollo del binomio los exponentes de a van disminuyendo, de uno en uno, de n a cero; y los exponentes de b van aumentando, de uno en uno, de cero a n, de tal manera que la suma de los exponentes de a y de b en cada término es igual a n.
En el caso que uno de los términos del binomio sea negativo, se alternan los signos positivos y negativos.

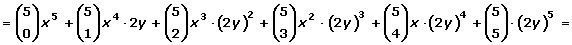
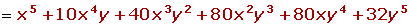
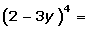
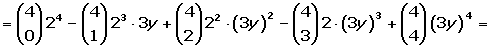
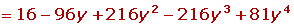
Cálculo del término que ocupa el lugar k

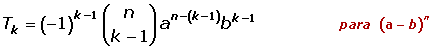
El término quinto del desarrollo de 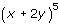
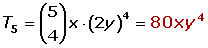
El término cuarto del desarrollo de 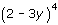
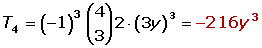
El término octavo del desarrollo de