Pendiente
La pendiente de la recta normal a una curva en un punto es la opuesta de la inversa de la pendiente de la recta tangente, por ser rectas perpendiculares entre sí.

La pendiente de la recta normal es la opuesta de la inversa de la derivada de la función en dicho punto.
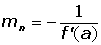
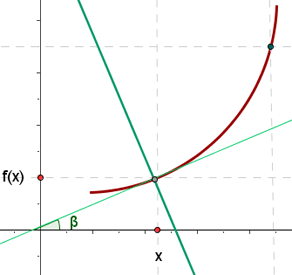
Ecuación de la recta normal
La recta normal a a una curva en un punto a es aquella que pasa por el punto (a, f(a)) y cuya pendiente es igual a la inversa de la opuesta de f '(a).
Ejemplos
Calcular la ecuación de la tangente y de la normal a la curva f(x) = ln tg 2x en el punto de abscisa: x = π/8.

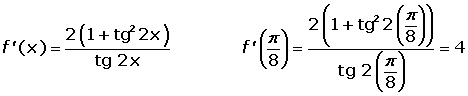


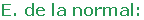

Hallar la ecuación de la recta tangente y normal a la parábola y = x2 + x + 1 paralela a la bisectriz del primer cuadrante.
Sea el punto de tangencia (a, b)
m = 1
f'(a) = 2a + 12a + 1 = 1 a = 0
Punto de tangencia:(0, 1)
Recta tangente:
y − 1 = x y = x +1
Recta normal:
m= 1P(0, 1)
y − 1 = −x y = −x + 1

