Temas
Unos grandes almacenes encargan a un fabricante pantalones y chaquetas deportivas. El fabricante dispone para la confección de 750 m de tejido de algodón y 1000 m de tejido de poliéster. Cada pantalón precisa 1 m de algodón y 2 m de poliéster. Para cada chaqueta se necesitan 1.5 m de algodón y 1 m de poliéster. El precio del pantalón se fija en 50 € y el de la chaqueta en 40 €.
¿Qué número de pantalones y chaquetas debe suministrar el fabricante a los almacenes para que estos consigan una beneficio máxima?
Solución:
1 Elección de las incógnitas
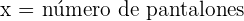
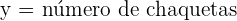
2 Función objetivo
3 Restricciones
Para escribir las restricciones vamos a ayudarnos de una tabla:
| pantalones | chaquetas | disponible | |
|---|---|---|---|
| algodón | 
| 
| 
|
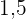
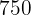
| poliéster | 
|
| 
|
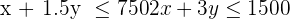
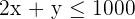
Como el número de pantalones y chaquetas son números naturales, tendremos dos restricciones más:
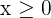
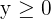
4 Hallar el conjunto de soluciones factibles
Tenemos que representar gráficamente las restricciones.
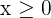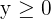Al ser e , trabajaremos en el primer cuadrante.
Representamos las rectas, a partir de sus puntos de corte con los ejes.
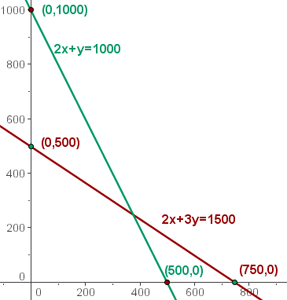
Resolvemos gráficamente la inecuación: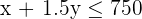 
, para ello tomamos un punto del plano, por ejemplo el 
.
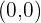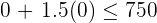
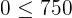entonces el punto 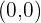se encuentra en el semiplano donde se cumple la desigualdad.
De modo análogo resolvemos .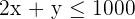
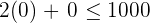
La zona de intersección de las soluciones de las inecuaciones sería la solución al sistema de inecuaciones, que constituye el conjunto de las soluciones factibles.
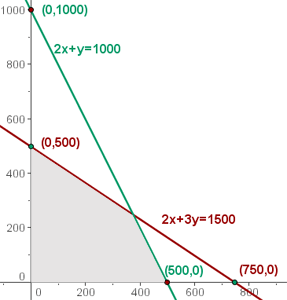
5 Calcular las coordenadas de los vértices del recinto de las soluciones factibles.
La solución óptima, si es única, se encuentra en un vértice del recinto. Estas son las soluciones a los sistemas:
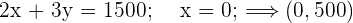
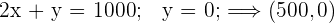
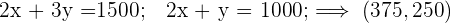
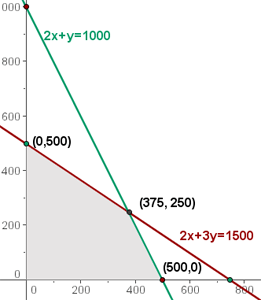
6 Calcular el valor de la función objetivo
En la función objetivo sustituimos cada uno de los vértices.
€
€
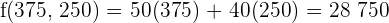€ entonces es un Máximo
La solución óptima es fabricar 375 pantalones y 250 chaquetas para obtener un beneficio de 28750 €.
Solución múltiple
La solución no siempre es única, también podemos encontrarnos con una solución múltiple.
Si la función objetivo del ejercicio anterior hubiese sido:
€ entonces es un Máximo
€
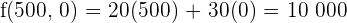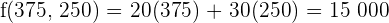€ entonces es un Máximo
En este caso todos los pares, con soluciones enteras, del segmento trazado en negro serían máximos.
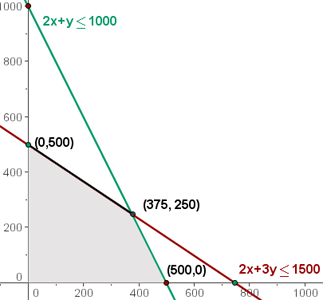
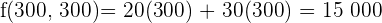€ Máximo
La plataforma que conecta profes particulares y estudiantes
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Buenas tardes me ayudaría con un ejercicio se lo podré aqui
Un granjero cría pavos, gallinas y patos. El costo de la crianza de una
gallina, un pato y un pavo es de 15, 10, y 40 unidades monetarias
respectivamente hasta el momento de su venta.
Las gallinas se venden a 30 unidades monetarias, los patos a 20 y los pavos
a 55 cada uno, sabiendo que la granja puede alojar solo a 500 aves y el
granjero no desea tener más de 300 patos a la vez. Cuantas aves de cada
especia debe criar a fin de maximizar las ganancias.
¡Hola!
Con gusto te ayudo con el problema. Primero acomodaré los datos en una tabla para una mejor visualización:
Nota que la cantidad de pavos la podemos representar en términos de ‘x’ e ‘y’ que son las cantidades de gallinas y pavos, respectivamente, tomando en cuenta que habrá 500 animales en total. Así, podemos dejar todo expresado en términos de 2 variables
Los costos totales de manutención de las aves los podemos expresar como:
Los ingresos como:
Y podemos expresar las ganancias sabiendo que
En este caso, las ganancias dependen únicamente de ‘y’, es decir del número de patos.
Nuestro programa de optimización sería:
Maximizar
s. a.
Pero podemos observar que la función de las ganancias es una recta con pendiente negativa y cuyo cruce con el eje vertical es 7500 u.m. El cruce con el eje vertical es el punto más alto que cumple la condición
, por lo que para maximizar las ganancias se requieren 0 patos.
En cuando a la cantidad de gallinas y pavos, puede ser cualquiera, siempre y cuando sumen 500.
Si observamos los datos iniciales, cada gallina representa un costo de 15 u.m. y un ingreso de 30 u.m., la ganancia por cada gallina es 15 u.m.
Por otro lado, la ganancia por cada pato es sólo de 10 u.m.
Y la ganancia por cada pavo es de 15 u.m.
Es decir, para maximizar las ganancia me conviene únicamente poseer gallinas y pavos, de modo que en total tenga 500 aves.
Espero que te sea de utilidad.
¡Saludos! 🙂
me podria ayudae con un ejercicio se prgramacion lineal de una tienda por favor
Hola me pueden ayudar con un ejercicio?.
Buenas me podrías dar un problema similar con ropa pero con minimización please
Hola Maria, gracias por el comentario. Añadiremos una nueva página de problemas pronto y incluiremos un problema con ropa. ¡Un saludo!
Utilice el método algebraico para calcular los valores de x e y que hacen máxima la función objetivo F (x, y) =40x+70y con las siguientes restricciones: x+y≤60; x+2y≤90; x≥0; y≥0.
Me ayudan por favor
Ayudenme cn el problema señala el o los numeros que comforman la grafica
me puede ayudar en un problema
Hola, escríbenos el enunciado del problema y te contestaremos lo más rápido posible. ¡Un saludo!
ayudeme con un ejemplo de progresion lineal de una tienda de abarrotes por favor
Hola me puedes ayudar con una pregunta
Ayudenme porfa
Esta en ingles n entiendo
Me pueden ayudar con la pregunta que se titula programacion lineal metodo grafico
Señala el o los numeros que conforman la grafica
Un estudiante dedica parte de su tiempo al reparto de
propaganda publicitaria. La empresa A le paga S/.5 por cada
impreso repartido y la empresa B, con folletos más grande, le
paga S/.7 por impreso. El estudiante lleva dos bolsas una para los
impresos A, en la que caben 120 y otra para los impresos B, en la
que caben 100. Ha calculado que cada día es capaz de repartir
150 impresos como máximo. Lo que se pregunta el estudiante es:
¿cuántos impresos habrá que repartir de cada clase para que su
beneficio diario sea máximo?
Hola,
denotamos por x al número de impresos de la empresa A y por y al número de impresos de la empresa B. La función objetivo es:
f(x,y)=(S/0.5)x+(S/0.7)y
Las restricciones vienen dadas por
x≥ 0,
y≥ 0
x≤ 120,
y≤ 100,
x+y≤ 150
La región formada por las restricciones tiene por extremos a los puntos: (0,100), (50, 100), (120, 30), (120, 0), (0, 0)
Sustituimos los extremos en la función objetivo
f(0,100)= (S/0.5)(0)+(S/0.7)(100)=(142.9)S,
f(50,100)= (S/0.5)(50)+(S/0.7)(100)=(242.9)S,
f(120,30)= (S/0.5)(120)+(S/0.7)(30)=(282.9)S,
f(120,0)= (S/0.5)(120)+(S/0.7)(0)=(240)S,
f(0,0)= (S/0.5)(0)+(S/0.7)(0)=0
Si S≥ 1, entonces los impresos que debe repartir a diario son 120 de la empresa A y 30 de la empresa B.
Espero te sea de utilidad.
Un saludo
Hola buenas noches me ayuda con un problema. Un asiduo cliente de una florería necesita para su fiesta de boda no menos de 100 claveles y 140 rosas. La florería dispone de dos tipos de diseños para estos eventos: el arreglo de mesa tipo bandeja con 3 claveles y 2 rosas, y el arreglo de mesa tipo jarrón con 2 claveles y 5 rosas. El arreglo floral tipo bandeja cuesta $12 mientras que el arreglo tipo jarrón cuesta $15. El cliente desea la mayor cantidad de flores en sus arreglos pero al menor precio posible. Calcula cuantos arreglos debe pedir.
es programación lineal , porfi ayúdeme
Alguien te pudo ayudar con este problema?
Ayudame por favor
Hola! Aqui les dejo los enunciados:
1.Una máquina funciona 8 horas al día. Hay 1000 gr de material diarios. La máquina fabrica piezas de tipo A que necesitan 50 gr y de tipo B que utilizan 100 gr. Las piezas de tipo A se cobran a 1,1 EUROS y las de tipo B a 1,4 EUROS. Para realizar las de tipo A se emplea 1 hora y en las de tipo B 0,5 horas. Escribe las restricciones que ha de cumplir el problema. ¿Cuántas unidades de cada tipo deben elaborar al día para maximizar sus ingresos?
2. Una fábrica de electrodomésticos tiene las siguientes funciones de ingresos y gastos, en euros, y dónde X es la cantidad de unidads vendidas
I(x) = 3x^4 + 7 x^2 +800x
G(x) = 3x ^4 +3x^2 +8000x+760000
a) La función que define el beneficio anual en euros. ¿Cuándo el beneficio es nulo?
b) Número de unidades vendidas que hace mínima la función de beneficio.
c) Intervalos de crecimiento y decrecimiento del beneficio.
¡Hola!
Con gusto te apoyo con la solución del problema:
Para el problema 1 comenzaremos con las restricciones
Como solo hay 1000 g de material disponible:
Como sólo funciona por 8 horas al día:
El ingreso diario estaría dado por:
No me es posible hacer el gráfico aquí, pero al graficar las restricciones y la función objetivo obtenemos que el máximo se obtiene en (4,8)
Lo que significa que hay que producir 4 piezas del tipo A y 8 del tipo B
El ingreso máximo sería:
2. Para el problema 2
Apartado a)
La función de beneficios se obtiene restando I(x)-G(x)
Para encontrar el beneficio nulo aplicamos la condición B(x)=0
Puede resolverse mediante la fórmula general y obtenemos:
Como ‘x’ no puede ser negativo nos quedamos solo con la solución
Apartado b)
Derivamos la función de beneficio e igualamos a cero
El mínimo está en x=900
Apartado c)
Como el mínimo está en x=900, la función para los valores antes de ese punto son decrecientes y después son crecientes, pero consideramos que para esta función x no puede ser negativo
Creciente:
Decreciente:
Espero que te sea de utilidad. No dudes en consultarnos para más preguntas que tengas.
¡Un saludo!
Buenas tardes, puede apoyarme con el siguiente problema: Don Chepe León dispone de 10 millones para repartir entre dos tipos de inversión (A y B). En la opción A desea invertir entre como mínimo dos millones, pero a la vez, no desea invertir más de siete millones en la misma opción. Además, quiere destinar a la opción B como mínimo tres millones.
Sabiendo que el rendimiento de la inversión será del 9 % en la opción A y del 12 % en la B, ¿Qué cantidad debe invertir en cada una para optimizar el rendimiento global? ¿A cuánto ascenderá dicho rendimiento?
ayudeme con un ejemplo de progresion lineal para una tienda
Hola serias muy amable de ayudarme, Una de las líneas de negocio de la empresa Laboratorio del Caribe se enfoca en la fabricación y comercialización de vacunas. En el plan de producción se proyecta producir un volumen X de la vacuna Gama con utilidad de $5000/litro y otro volumen Y de vacuna Beta con utilidad de $3000/litro. La empresa dispone de 15 personas en la planta de producción y un presupuesto de de $10.000 para esta actividad. A continuación, se detallan los recursos necesarios para la fabricación de cada una de las vacunas
Hola buenos días, me podrías ayudar a sacar la función objetivo
La empresa VIDEOGAMER Co., cuenta con tres videojuegos, la utilidad del videojuego arcade es de USD170, del videojuego de estrategia es de USD140 y del videojuego de simulación es de USD150. El costo de desarrollo del videojuego arcade es de USD110, del videojuego de estrategia es de USD90 y del videojuego de simulación es de USD100 y la empresa cuenta con un capital inicial máximo para invertir en el desarrollo de estos videojuegos de USD500.000. Los videojuegos se deben jugar en línea, para ello la empresa dispone de un servidor con una Tera (125.000.000 kb) de capacidad máxima para almacenar la información de los videojuegos, en promedio, el videojuego arcade consume 20.000 kb, el videojuego de estrategia consume 50.000 kb y el videojuego de simulación consume 17.000 Kb. Además, la empresa cuenta con personal experto en el desarrollo del software, los cuales deben repartir su tiempo para lograr un buen producto, 10 h/hombre para el videojuego arcade, 5 h/hombre para el videojuego de estrategia y 10 h/hombre para el videojuego de simulación y en total se dispone máximo de 20.000 h/hombre para los desarrollos. 3 ¿Cuántos videojuegos de cada tipo debe vender la empresa VIDEOGAMER Co. en el lanzamiento, para obtener la mayor utilidad posible con los recursos disponibles?
Llevo esto, pero no se si esta bien
170×1+140×2+150×3 =500000
20000×1+50000×2+17000×3 = 125000
10×1+5×2+10×3 = 20000
Hola,
me alegra ver que hayas avanzado en tu planteamiento. A los dos últimos les faltó es símbolo de menor, mientras que en el primero se encuentra la función objetivo (utilidad) por lo que no debes igualarlo a 500,000 (costo). El planteamiento es
Función objetivo
Restricciones
Espero haber sido de ayuda.
Un saludo.
Hola me ayudarían con este ejercicio,
Se está creando una clínica. La ley dice que no puede haber más doctores que enfermeras (a lo sumo la cantidad debe ser igual). Disposiciones sindicales establecen que la cantidad de enfermeras no puede superar al doble de doctores. Tenemos el curriculum de 30 doctores y 20 enfermeras. Estos profesionales generan a la clínica diariamente 250 UF por doctor y 200 UF por enfermera. ¿Cuántos doctores y cuántas enfermeras contratar para maximizar la utilidad de la clínica?
si, son 20 pesos
«Los Robinsons están planeando una boda y una recepción para su hija, Rachel. Algunos de los artículos más caros que se sirven en la recepción y la cena son el vino y la cerveza. Los Robinsons están planeando 200 invitados en la recepción, y estiman que necesitan al menos cuatro porciones (es decir, un vaso de vino o una botella de cerveza) para cada invitado para asegurarse de que no se les acabará. Una botella de vino contiene cinco vasos. También estiman que el 50% más de los huéspedes preferirán el vino a la cerveza. Una botella de vino cuesta 8 dólares y una de cerveza 0,75 dólares. Los Robinsons han presupuestado 1,200 dólares por el vino y la cerveza. Finalmente, los Robinsons quieren minimizar sus residuos (es decir, el vino sin usar y la cerveza). El catering les ha aconsejado que normalmente el 5% del vino y el 10% de la cerveza sobran. ¿Cuántas botellas de vino y cerveza deben pedir los Robinsons?
a. Formular un modelo de programación lineal para este problema.
b. Resolver este modelo gráficamente y concluir»
La ecuacion resultante como se escribe
F500 no existe
Hola! me podria ayudar con este problema?
El Hotel Star quiere aumentar el precio de dos de sus habitaciones para aumentar su margen de utilidad a partir de sus ingresos. Para determinar la elasticidad precio de la demanda ha contratado a un analista, al cual se le entrega la siguiente información con respecto a la función de demanda: J. Suite q= 225-0.30p y Familiar q= 245-0.20p
Encuentra el precio en el que se maximice el ingreso.
Cuanto es el ingreso máximo que puede tener la empresa con cada precio por habitación.
Hola, me podrían ayudar a pasar esta restricción a términos matematicos.
La producción de vino debe ser mínimo 500 botellas.
Rendimiento de gasolina el rendimiento de gasolina g (medido en millar/gal) para auto en particular, manejado a v mi/h, está dada por la formula g = 10 + 0.90 -0.01v, mientras v esté entre 10 mi/h. ¿Para que intervalo de velocidad el rendimiento del vehículo será de 30 mi/gal o mejor?
Lo necesito URGENTE!
2. Diseñe un pseudocódigo e implemente un algoritmo que le permita generar un arreglo unidimensional, de productos petroquímicos de 5 hidrocarburos; los cuales, deben ser ingresados por teclado; ordene el arreglo ascendentemente aplicando cualquier método; a continuación, busque un hidrocarburo en el arreglo, si no se encuentra el hidrocarburo en el arreglo deberá imprimir un aviso “EL HIDROCARBURO NO SE ENCUENTRA EN EL ARREGLO”, y si el hidrocarburo se encuentra en el arreglo deberá imprimir un aviso “EL HIDROCARBURO SE ENCUENTRA EN EL ARREGLO, EN LA POSICIÓN: ”; adicionalmente, diseñe e implemente la opción: ¿DESEA CONTINUAR SI/NO?. Para salir del sistema, imprima un mensaje “El Sistema de los Productos Petroquímicos ha Finalizado su Procesamiento”.
Una cooperativa tiene una finca de 300 hectáreas que puede bombear un millón de metros cúbicos del
acuífero adyacente. La cooperativa quiere usar la totalidad de la finca con fines agropecuarios y proyecta
producir plátano y maíz y también sembrar pasto de pastoreo para la cría de ganado. Una hectárea de
plátano requiere 10 mil metros cúbicos de agua y 40 horas de mano de obra. Una hectárea de maíz
requiere cuatro mil metros cúbicos de agua y 12 horas de mano de obra. Una cabeza de ganado requiere
media hectárea de pasto, 100 metros cúbicos de agua (incluyendo el agua para el pasto) y ocho horas de
mano de obra. La cooperativa dispone de un capital de 100 millones de pesos y un total de ocho mil horas
de mano de obra. Los costos de producción de una hectárea de plátano y de una de maíz son 500.000 UM
y 100. UM respectivamente, mientras que la producción de ganado cuesta 70.000 UM por cabeza. El
ingreso bruto anual de la cooperativa es de 1.100.000 UM por hectárea de plátano y de 300.000 UM por
hectárea de maíz. Una cabeza de ganado después de un año de engorde vale 130.000 UM. Determinar el
número máximo de cabezas de ganado y las hectáreas de plátano y maíz que maximizan la ganancia neta
de la cooperativa.
En una confitería se dispone de 24 kg de almendras y 15 kg de pecanas, que
se envasan en dos tipos de cajas de la siguiente forma:
– Caja 1: 200 g de almendras y 100 g de pecanas. Precio: 400 soles.
– Caja 2: 200 g de almendras y 300 g de pecanas. Precio: 600 soles.
¿Cuántas cajas de cada tipo se tendrán que preparar y vender para obtener el
máximo de ingresos?
Hola buenas tardes, me podrian ayudar con un ejercicio por favor, una compañía dispone de 200kg de cachuates, 40 kg de almendras y 20 kg de nueces. Empaca 4 tipos de latas de 400 gramos con estas semillas procesadas, la lata 1 tiene 200 gramos de cacahuetes, 100 gramos de almendras y 100 gramos de nueces, la lata 2 contiene 300 gramos de cacahuetes y 100 gramos de almendras, la lata 3 contiene 400 gramos de cacahuetes. Las latas 1,2 y 3 se venden en $80, $60 y $40 respectivamente. Cuantas latas de cada tipo debe empacar la compañía para maximizar sus ingresos?
Buenas noches: Podría usted ser tan amable y me ayuda a resolver los problemas que a continuación le escribiré; quedaré altamente agradecido.
PRIMER EJERCICIO
1. Un problema de maximización tiene la siguiente información:
Z = 1200X1 + 1450X2
SA:
60X1+30X2 < 1500
5X1+10X2 < 200
50X1+80X2 0
Elija cual es la solución viable en la mezcla de X1 y X2.
(a). 16.18X1 – 17.63X2
(b). 20X1 – 10×2
(c). 25X1 – 0X2
SEGUNDO EJERCICIO
2. Dados los siguientes datos de un problema de programación lineal, solucione por método gráfico y elija la solución viable al problema de minimización:
VARIABLES DE DECISIÓN: X1, X2
Fo: Min Z= 120X1 + 420X2
SA:
2000X1 + 4000X2 > 6000
50X1 + 200X2 > 200
(a). PRODUCIR 3 DE X1 Y 0 DE X2
(b). PRODUCIR 2 DE X1 Y 0.5 DE X2
(c). PRODUCIR 0 DE X1 Y 1 DE X2
De todo corazón, muchas gracias.
hola buenas noches me podría hacer favor de ayudarme con este problema
Una empresa entregara a un cliente 1000 mantas de ixtle. La empresa se dispone para la confección de 122,000 mts. de tela de ixtle. Cada manta precisa 1.220 kg de ixtle Para cada manta se necesitan 980 mts de hilo ixtle y el hilo vale 90 pesos el kg
¿Qué número de hilo de ixtle debe utilizarla empresa para elaborar 1000 mantas
Buenas tardes! Me ayudarían con un problema? Es un problema de programación lineal por método de Simplex.
x1 + 3×2
x1 – x2 >igual 0
x1 >igual 2
Encontrar el mínimo de los costos que se tiene al fabricar el producto X1 y X2, en los cuales se tiene costo por producir el producto X1 de $4.00 y de $1.00 el producto X2. El proceso de fabricación está sujeto a las siguientes ecuaciones que involucran inventario de materia prima:
Una distribuidora de cartuchos para impresora que da servicio a domicilio tiene
dos ocinas y tres clientes ubicados en diferentes puntos de la ciudad. Los costos
unitarios de transporte se muestran en la siguiente tabla:
Cliente 1 Cliente 2 Cliente 3
Ocina 1 4 3 8
Ocina 2 2 5 5
En cada ocina tienen 10 y 20 cartuchos de impresora respectivamente y cada
cliente requiere al menos 7 cartuchos. Con esta información se desea conocer la
combinación óptima de envíos para tener un costo de distribución mínimo.
Para este planteamiento se observa que las desigualdades asociadas a las
restricciones del modelo pueden plantearse como 21 ≤ “número de cartuchos
enviados” ≤ 30, que en realidad son dos desigualdades.
Un puesto de zumos vende dos tipos de zumo fresco en vasos de 12 onzas, el Refresher y el Super-Duper. El Refresher está hecho con 3 naranjas, 2 manzanas y una rodaja de jengibre. El Super Duper se hace con una rodaja de sandía, 3 manzanas y una naranja. Los propietarios del puesto de zumos tienen 50 naranjas, 40 manzanas, 10 rodajas de sandía y 15 rodajas de jengibre. Sea x el número de Refrescos que hacen y sea y el número de Súper-Dupers que hacen.
Programacion lineal metodo grafico ejemplos
Buen día alguien me podría plantear y resolver un problema sobre programación lineal con el tema de las vacunas de covid-19 ?
Hola me puedes ayudar a entender esta situación.
no me quedan muy claras las restricciones.
El encargado de una tienda de ropa desea saber cuáles son sus utilidades en la producción y venta de los siguientes productos:
● El costo de producir un pantalón de mezclilla con decoraciones es de $80.
● El costo de producir una camisa de algodón con estampado es de $35.
Para la producción de un pantalón se consumen 2 horas a la semana más media hora de empaque. Para elaborar una camisa de algodón se necesita 1 hora, incluyendo el empaque. La cantidad de hilo para la elaboración del pantalón debe ser igual o menor a 3 carretes y para la camisa de algodón debe ser igual o menor a 0.5 carretes. El precio de venta del pantalón es de $200 y el de la camisa de $90
algo no estoy entendiendo, saludos
El problema está mal planteado
ayudenme con este ejercicio.- En una fábrica de cajas de cartón para embalaje y regalo, se fabrican dos tipos de cajas: la caja A
que requiere para su construcción 4 m. papel decorado y 0.25 m. de rollo de cartón, que se
vende a 8 €; la caja B que requiere 2 m. de papel decorado y 0.5 m. de rollo de cartón y que se
vende a 12 €. En el almacén disponen únicamente de 440 m. de papel de regalo y de 65 m. de
rollo de cartón. Si suponemos que se vende toda la producción de cajas, ¿cuantas de cada tipo
deberán de fabricarse para que el importe de las ventas sea máximo? ¿A cuánto ascenderá?
LA MESCLA FRUTOS SECOS POR 3.25KG TIENE UN COSTO DE $19564EL KILO. SI EL KILO DE NUECES TIENE UN PRECIO DE $14300 Y LAS ALMENDRAS $23500 ¿CUANTO ES LA CANTIDAD DE NUECES Y ALMENDRAS EN LA MESCLA FINAL?
cantidad de kg de nueces?
cantidad de kilogramos de almendras?
Disculpe que pasaria si solo tivieramos la funcion de obejtivo y nos pide encontrar todos los vertices pero uno no esta en un punto marcado exactamenente?
Se supone que con las restricciones no habría ese problema, pero si no esta marcado exactamente entonces seria cuestión de hacer una aproximación dando valores cercanos.
Me pueden ayudar en un ejercicio?
HOLA ME PODRIAN AYUDAR CON UN EJRCICIO PORFAVOR,
Un fabricante desea planear la producción de dos artículos A y B para los meses de marzo, abril, mayo y junio.
Las demandas que se deben satisfacer son las siguientes:
ARTICULO MARZO ABRIL MAYO JUNIO
A 400 500 600 400
B 600 600 700 600
Suponer que el inventario de A y B al finalizar el mes de febrero es de 100 y 150, respectivamente. Suponga,
además, que al final del mes junio se debe disponer de, al menos, 150 unidades del artículo B. Los costos de
almacenaje de las unidades no vendidas de los artículos A y B durante cualquier mes son de $1 y $0,80
multiplicados por el inventario del artículo respectivo al final del mes. Por otra parte, debido a limitaciones de
espacio, la suma de los artículos A y B en almacén no puede exceder de 250 durante cualquier mes. Finalmente, el
número máximo de artículos A y B que se pueden producir durante un mes dado es de 500 y 600,
respectivamente.
Formular el problema de producción. El objetivo consiste en minimizar el costo total de inventario (el costo de
producción se supone constante).
PORFAVOR ESPERO SU AYUDA4
anecesito una ayuda con este ejercicio si alguien me puede colaborar estare muy agradecido
fabricante de productos informáticos y elabora 4 tipos de discos
duros cuyas demandas se han estimado dentro de unos márgenes mínimos y máximos. Se
observan las siguientes características del proceso de producción y sus ventas:
• Los tiempos necesarios para producir cada tipo de disco son diferentes.
• Las materias primas necesarias para la fabricación son las mismas para todos los discos,
siendo estas 5. Se conocen los gastos de fabricación por unidad.
• Hay 3 suministradores de las materias primas que las venden a distinto precio al
fabricante. Este desea, por razones políticas, comprar a los 3 dentro de unos límites
mínimos y máximos.
• Hay una capacidad limitada de almacenamiento para las materias primas, pero no para
los discos fabricados.
• Los costos de fabricación están determinados, básicamente, por la adquisición de
materias primas y los de mano de obra, ambos conocidos.
Se desea formular un modelo de programación lineal resumido (notación matemática) que
determine la cantidad de discos duros
Puede ayudarme por favor con esto:
Ejemplo de Programación Lineal con 2 variables.
Gracias
Hola buenas noches me ayudarías con un problema por favor, se lo pondré aquí:
Para la fabricación de dos productos, se utilizan dos tipos de materiales M1 y M2 para la fabricación de dichos productos, P1 y P2. La disponibilidad de los materiales M1 y M2 es de 135 y 120 toneladas, en su orden. El producto P1 contiene el 30% de M1 y 40% de M2; mientras que el producto P2 contiene el 70% de M1 y 60% de M2. Las utilidades unitarias de los productos P1 y P2 son $3 y $5, respectivamente. La demanda del producto P1 está entre 25 y 130 unidades y la de P2 entre 35 y 150 unidades ¿Cuántos productos de cada uno se debe fabricar para maximizar sus utilidades?
1. Se va a establecer una empresa de computación donde van a trabajar informáticos y
ensambladores. Por necesidades del mercado, es necesario que haya mayor o igual
número de ensambladores que de informáticos y que el número de ensambladores no
supere al doble que el de informáticos. En total hay disponible 60 informáticos y 40
ensambladores.
El beneficio de la empresa por jornada es de $300 para informáticos y $240 para
ensambladores. ¿Cuánta mano de obra de cada clase deben elegirse para obtener el
máximo beneficio?
Porfa ayuda con este ejercicio
Me podría ayudar con este ejercicio
Un gerente de finanzas tiene $2,500,000 en un fondo de pensiones, todo o parte del cual debe invertirse. El gerente tiene dos inversiones en mente, unos bonos conservadores que producen 5.5% anual y unos bonos hipotecarios más riesgoso que producen 11% anual. De acuerdo con las regulaciones del gobierno, no más del 30% de la cantidad invertida puede estar en bonos hipotecarios. Mas aún, lo mínimo que puede ponerse en bonos hipotecarios es de $300,000. Determine las cantidades de las dos inversiones que maximizarían la inversión total. ¿Cuál es la inversión total anual?
hola me pueden ayudar con un problema. La mayoría de los departamentos académicos de las universidades contratan estudiantes para que realicen encargos de oficina. La necesidad de ese servicio fluctúa durante las horas hábiles (8:00 A.M. a 5:00 P.M.). En un departamento, la cantidad mínima de estudiantes requeridos es de 2 entre las 8:00 A.M. y las 10:00 A.M.; 3 entre las 10:01 A.M. y las 11:00 A.M.; 4 entre las 11:01 A.M. y la 1:00 P.M., y 3 entre la 1:01 P.M. y las 5:00 P.M. A cada estudiante se le asignan 3 horas consecutivas (excepto a los que inician a las 3:01 P.M. que trabajan 2 horas, y a los que inician a las 4:01 que trabajan 1 hora). Debido al horario flexible de los estudiantes, por lo común pueden iniciar a cualquier hora durante el día de trabajo, excepto a la hora del almuerzo (12:00 del día). Desarrolle el modelo de PL.
Saludos Cordiales.
Me gustaría saber si me pueden ayudar con la solución de la siguiente programación lineal.
En una zapatería se encargan de fabricar zapatos casuales y zapatos deportivos. El fabricante de zapatos dispone de la confección de 150 m de suela negra y 100 m de suela blanca. Cada zapato es de una precisa 1 cm de suela blanca y 2 cm de suela negra. Sin embargo, Para cada zapato se necesitan 1.5 cm de suela blanca y 1 cm de suela negra. El precio de cada zapatos casuales se fija entre 50 $ y el de zapatos deportivos en 30 $.
– ¿Qué número de zapato casuales y zapatos deportivos debe suministrar el fabricante a los almacenes para que éstos consigan una venta máxima?
– Hallar el 3 conjuntos de soluciones factibles.
– Calcular las coordenadas de los vértices del recinto de cada solución factible.
mUY BUENOS EJEMPLOS Y DESARROLLO, APENAS VOY EMPEZANDO EN ESTO Y ES BUENO CONTAR CON PAGINAS COMO ESTAS QUE NOS AYUDAN MUCHO
muchas gracias
Buenos dias me ayudaría con un ejercicio se lo podré aqui Una de las líneas de negocio de la empresa Laboratorio del Caribe se enfoca en la fabricación y comercialización de vacunas. En el plan de producción se proyecta producir un volumen X de la vacuna Gama con utilidad de $5000/litro y otro volumen Y de vacuna Beta con utilidad de $3000/litro. La empresa dispone de 15 personas en la planta de producción y un presupuesto de de $10.000 para esta actividad. A continuación, se detallan los recursos necesarios para la fabricación de cada una de las vacunas
hola soy cristina y necesito que me ayudes con un ejemplo de aplicación de programación lineal en un servicio de enfermería dé un hospital
buenos ejercicios alguien me puede ayudar con un ejercicio