Dos vectores Explicaciones y ejemplos de base vectorial - 1 y Explicaciones y ejemplos de base vectorial - 2 con distinta dirección forman una base, porque cualquier vector del plano se puede poner como combinación lineal de ellos.

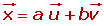
Explicaciones y ejemplos de base vectorial - 3

Explicaciones y ejemplos de base vectorial - 4


Las coordenadas del vector respecto a la base son:

Explicaciones y ejemplos de base vectorial - 5

Ejemplos

Explicaciones y ejemplos de base vectorial - 6

Explicaciones y ejemplos de base vectorial - 7

Los dos vectores que forman una base no pueden ser paralelos.

Ejemplo

Qué pares de los siguientes vectores forman una base:

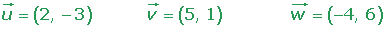
Explicaciones y ejemplos de base vectorial - 8

Explicaciones y ejemplos de base vectorial - 9

Explicaciones y ejemplos de base vectorial - 10

Explicaciones y ejemplos de base vectorial - 11

Base ortogonal

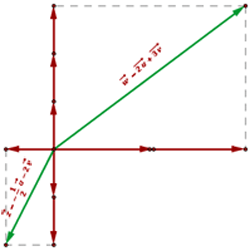
Explicaciones y ejemplos de base vectorial - 12

Los dos vectores de la base son perpendiculares entre sí.

Base ortonormal

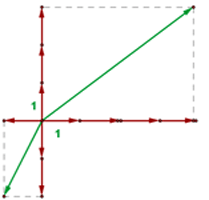
Explicaciones y ejemplos de base vectorial - 13


Los dos vectores de la base son perpendiculares entre sí, y además tienen módulo 1.

Explicaciones y ejemplos de base vectorial - 14

Explicaciones y ejemplos de base vectorial - 15

Explicaciones y ejemplos de base vectorial - 16

Esta base formada por los vectores Explicaciones y ejemplos de base vectorial - 17 y Explicaciones y ejemplos de base vectorial - 18 se denomina base canónica.

Es la base que se utiliza habitualmente, de modo que si no se advierte nada se supone que se está trabajando en esa base.


Bases en el espacio

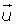
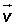
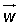
Tres vectores Explicaciones y ejemplos de base vectorial - 19, Explicaciones y ejemplos de base vectorial - 20 y Explicaciones y ejemplos de base vectorial - 21 con distinta dirección forman una base, porque cualquier vector del espacio se puede poner como combinación lineal de ellos.

Explicaciones y ejemplos de base vectorial - 22

Las coordenadas del vector respecto a la base son:

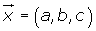
Explicaciones y ejemplos de base vectorial - 23

Base ortogonal

Una base es ortogonal si los vectores de la base son perpendiculares entre sí.

Base ortonormal

Una base es ortonormal si los vectores de la base son perpendiculares entre sí, y además tienen módulo 1.

Explicaciones y ejemplos de base vectorial - 24

Explicaciones y ejemplos de base vectorial - 25

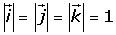
Explicaciones y ejemplos de base vectorial - 26

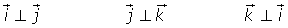
Explicaciones y ejemplos de base vectorial - 27

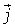
Esta base formada por los vectores Explicaciones y ejemplos de base vectorial - 28, Explicaciones y ejemplos de base vectorial - 29 y Explicaciones y ejemplos de base vectorial - 30 se denomina base canónica.

Ejercicios en el plano

Qué pares de los siguientes vectores forman una base:

Explicaciones y ejemplos de base vectorial - 31

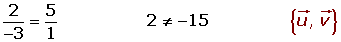
Explicaciones y ejemplos de base vectorial - 32

Explicaciones y ejemplos de base vectorial - 33

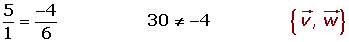
Explicaciones y ejemplos de base vectorial - 34


Sean los vectores libres Explicaciones y ejemplos de base vectorial - 35 = (2, 1), Explicaciones y ejemplos de base vectorial - 36 = (1, 4) y Explicaciones y ejemplos de base vectorial - 37 = (5, 6). Determinar:

1.

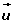
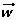
Si forman una base Explicaciones y ejemplos de base vectorial - 38 y Explicaciones y ejemplos de base vectorial - 39.

Explicaciones y ejemplos de base vectorial - 40

2.

Expresar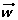 Explicaciones y ejemplos de base vectorial - 41 como combinación lineal de los de la base

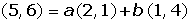
Explicaciones y ejemplos de base vectorial - 42

Explicaciones y ejemplos de base vectorial - 43

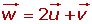
Explicaciones y ejemplos de base vectorial - 44

3.

Calcular las coordenadas de C respecto a la base.

Las coordenadas de 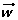Explicaciones y ejemplos de base vectorial - 45 respecto a la base son: (2, 1)


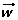
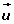
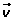
Un vector Explicaciones y ejemplos de base vectorial - 46 tiene de coordenadas (3, 5) en la base canónica. ¿Qué coordenadas tendrá referido a la base Explicaciones y ejemplos de base vectorial - 47 = (1, 2), Explicaciones y ejemplos de base vectorial - 48 = (2, 1)?

(3, 5) = a (1, 2) + b (2, 1)

3 = a + 2b a = 3 - 2b a = 7/3

5 = 2a + b 5 = 2 (3 - 2b) + b b = 1/3

Las coordenadas de 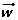Explicaciones y ejemplos de base vectorial - 49 en la base B son (7/3, 1/3).


Ejercicios en el espacio

1.

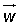
Dados los vectores Explicaciones y ejemplos de base vectorial - 50 = (1, 2, 3), Explicaciones y ejemplos de base vectorial - 51 = (2, 1, 0) y Explicaciones y ejemplos de base vectorial - 52 = (−1, −1, 0), demostrar que dichos vectores forman una base y calcula las coordenadas del vector (1, −1, 0) respecto de dicha base.

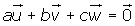
Explicaciones y ejemplos de base vectorial - 53

Explicaciones y ejemplos de base vectorial - 54

Explicaciones y ejemplos de base vectorial - 55

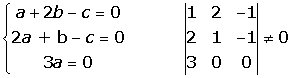
Explicaciones y ejemplos de base vectorial - 56

El sistema homogéneo sólo admite la solución trivial:

Explicaciones y ejemplos de base vectorial - 57

Por tanto, los tres vectores son linealmente independientes y forman una base.

Explicaciones y ejemplos de base vectorial - 58

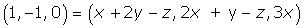
Explicaciones y ejemplos de base vectorial - 59

Explicaciones y ejemplos de base vectorial - 60

Las coordenadas del vector (1, −1, 0) respecto a la base son: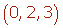Explicaciones y ejemplos de base vectorial - 61.


2.

Dados los vectores: (1, 1, 0), (1, 0, 1) y (0, 1, 1).

1

Demostrar que forman una base.

Los tres vectores forman una base si son linealmente independientes.

Explicaciones y ejemplos de base vectorial - 62

Explicaciones y ejemplos de base vectorial - 63

Explicaciones y ejemplos de base vectorial - 64

En el sistema homogéneo el rango coincide con el número de incógnitas, por tanto tan sólo admite la solución trivial:

Explicaciones y ejemplos de base vectorial - 65

Los vectores son linealmente independientes y, por tanto, forma una base.

2

Hallar las coordenadas de los vectores de la base canónica respecto de esta base.

Las coordenadas de los vectores de la base canónica respecto de la base son:

Explicaciones y ejemplos de base vectorial - 66

Explicaciones y ejemplos de base vectorial - 67

Explicaciones y ejemplos de base vectorial - 68

Explicaciones y ejemplos de base vectorial - 69

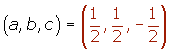
Explicaciones y ejemplos de base vectorial - 70

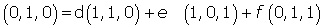
Explicaciones y ejemplos de base vectorial - 71

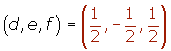
Explicaciones y ejemplos de base vectorial - 72

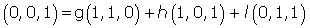
Explicaciones y ejemplos de base vectorial - 73

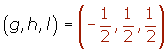
Explicaciones y ejemplos de base vectorial - 74


3.

Calcular el valor de a para que los vectores Explicaciones y ejemplos de base vectorial - 75, Explicaciones y ejemplos de base vectorial - 76y Explicaciones y ejemplos de base vectorial - 77 formen una base.

Explicaciones y ejemplos de base vectorial - 78

Si a ≠ 1, los vectores forman una base.