Capítulos

Relación funcional
Dos variables x e y están relacionadas funcionalmente cuando conocida la primera se puede saber con exactitud el valor de la segunda.
Ejemplos
Si se deja caer una piedra, existe una fórmula que nos permite calcular exactamente, la altura a la que se encuentra en función del tiempo transcurrido.
h = ½ g t².
Relación estadística
Dos variables x e y están relacionadas estadísticamente cuando conocida la primera se puede estimar aproximadamente el valor de la segunda.
Ingresos y gastos de una familia.
Producción y ventas de una fábrica.
Gastos en publicidad y beneficios de una empresa.
Variable estadística bidimensional
Una variable bidimensional es una variable en la que cada individuo está definido por un par de caracteres, (X, Y).
Estos dos caracteres son a su vez variables estadísticas en las que sí existe relación entre ellas, una de las dos variables es la variable independiente y la otra variable dependiente.
Distribuciones bidimensionales
Son aquellas en las que a cada individuo le corresponden los valores de dos variables, las representamos por el par (xi, yi).
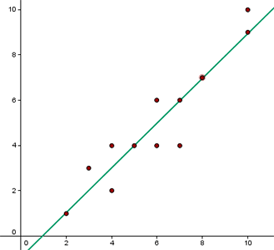
Si representamos cada par de valores como las coordenadas de un punto, el conjunto de todos ellos se llama nube de puntos o diagrama de dispersión.
Sobre la nube de puntos puede trazarse una recta que se ajuste a ellos lo mejor posible, llamada recta de regresión.
Las notas de 12 alumnos de una clase en Matemáticas y Física son las siguientes:
| Matemáticas | Física |
| 2 | 1 |
| 3 | 3 |
| 4 | 2 |
| 4 | 4 |
| 5 | 4 |
| 6 | 4 |
| 6 | 6 |
| 7 | 4 |
| 7 | 6 |
| 8 | 7 |
| 10 | 9 |
| 10 | 10 |
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
En el cuarto ejercicio todas las ecuaciones concuerda, menos la primera ecuación, entonce cómo sabe que la tercera es la que pide
hola se menciona que «Como el coeficiente de correlación lineal es negativo, la pendiente de la recta también será negativa, por tanto se descarta ecuación 2 y 4» pues sus pendientes son 3 y 1, mientras la ecuación 3 si cumple pues su pendiente es -2.
Muchas gracias por la clara explicación de los 12 alumnos. Para mi, tienes 5 estrellas
solo que no he sabido despejar el polinomio
y – 5 = (5.92 / 6) * (x – 6) >>> y = 0.987 * x – 0.922
Para hallar la intercepción (-0.922) se me ha ocurrido que
como la recta siempre tiene que pasar exactamente por el punto de las medias
y como ya sabemos la media de y (5) y el coeficiente de x (0.987)
me basta con aplicarle el coeficiente a la media de x
y sacar la diferencia a la media de y.
intercepción = 5 – (0.987 * 6) = -0.922
Muy bien, otra manera es hacer x=0 y encontrar el valor de y.
En el ejercicio 1 la ecuación de la recta es: x=0,192 y-0,84
Ya revise el ejercicio y la ecuación es y=0.53x+302.91
Quisiera saber de donde sale el 0.53 del primer ejercicio
De dividir 22.8/42.58 o σy/σx.
Hola…muy bueno solo tengo una duda… ¿No debería ser sigma y sobre sigma cuadrado x?
Gracias
Hola gracias por tu aportación, podrías darnos mas detalles para corregir el error, por ejemplo si es en un ejercicio y el número de este.