¡Bienvenidos a nuestra página especializada en ejercicios de regresión y correlación! La regresión y la correlación son herramientas fundamentales en el análisis de datos, utilizadas en una amplia gama de campos, desde la investigación científica hasta la toma de decisiones empresariales.
En este artículo, te sumergirás en una variedad de ejercicios prácticos diseñados para ayudarte a comprender y aplicar conceptos clave relacionados con la regresión y la correlación. Aquí encontrarás ejemplos claros y desafiantes en los cuales tendrás que encontrar la ecuación de la recta de regresión, calcular el coeficiente de correlación lineal , calular la varianza, covarianza, y más.
Acompáñanos en este viaje educativo mientras desmitificamos la estadística y te equipamos con las habilidades necesarias para interpretar datos, identificar relaciones significativas y tomar decisiones informadas. ¡Comencemos a explorar el vínculo entre variables y a dominar los ejercicios de regresión y correlación!
La covarianza se representa por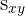 
ó 
y viene dada por las expresiones
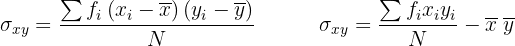
Cinco niños de 2, 3, 5, 7 y 8 años de edad pesan, respectivamente, 14, 20, 32, 42 y 44 kilos.
1Hallar la ecuación de la recta de regresión de la edad sobre el peso.
2¿Cuál sería el peso aproximado de un niño de seis años?
 |  |  |  |  |
|---|---|---|---|---|
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
|  |  |  |  |
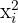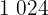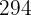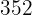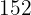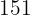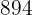Calculamos los promedios
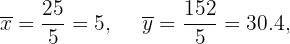
Calculamos la covarianza y la varianza de 
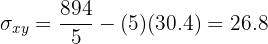
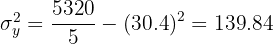
La recta de regresión de la edad sobre el peso es aquella que pasa por el punto 
y tiene pendiente 
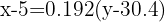
Despejamos y obtenemos la recta de regresión
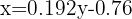
Para encontrar el peso aproximado de un niño de seis años, sustituimos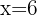 
en la ecuación de regresión y obtenemos
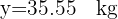
Un centro comercial sabe en función de la distancia, en kilómetros, a la que se sitúe de un núcleo de población, acuden los clientes, en cientos, que figuran en la tabla:
Nº de Clientes 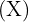 | Distancia  |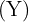
|  |
|  |
 | |
|  |
|  |
 |  |
1Calcular el coeficiente de correlación lineal.
2Si el centro comercial se sitúa a km, ¿cuántos clientes puede esperar?
3Si desea recibir a clientes, ¿a qué distancia del núcleo de población debe situarse?
| | | | |
|---|---|---|---|---|
| |  | |  |
| |  | |  |
| |  |  |  |
| |  |  |  |
| |  | |  |
| | | |  |
|  |  |  |  |
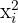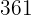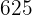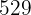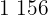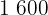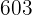Calculamos los promedios
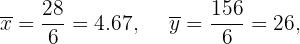
Calculamos la covarianza, las varianza y las desviaciones estándares
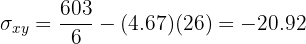
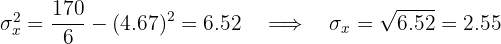
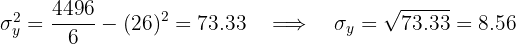
El coeficiente de correlación está dado por
Se tiene una correlación negativa muy fuerte.
La recta de regresión de los clientes sobre la distancia, es aquella que pasa por el punto y tiene pendiente
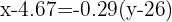
Despejamos y obtenemos la recta de regresión
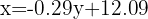
Para encontrar el número de clientes cuando el centro comercial se sitúa a 2 kilómetros, sustituimos 
en la ecuación de regresión y obtenemos
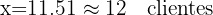
Si se desea recibir cinco clientes, sustituimos 
en la ecuación de regresión y obtenemos
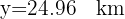
Las notas obtenidas por cinco alumnos en Matemáticas y Química son:
| Matemáticas | Química |
|  |
|  |
| |
| |
 | |
Determinar las rectas de regresión y calcular la nota esperada en Química para un alumno que tiene 
en Matemáticas.
| | | | |
|---|---|---|---|---|
| | |  |  |
| | |  |  |
| | | |  |
| | | | |
| |  | | |
 |  |  |  | |
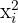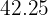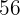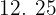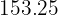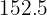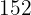Calculamos los promedios
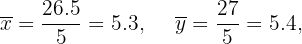
Calculamos la covarianza y la varianza de
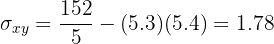
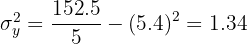
La recta de regresión de la calificación de matemáticas sobre la calificación de química, es aquella que pasa por el punto y tiene pendiente
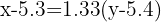
Despejamos y obtenemos la recta de regresión
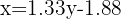
De esta misma despejamos y obtenemos la recta de regresión en términos de la calificación en matemáticas
Para encontrar la nota esperada en química para un alumno que tiene siete punto cinco en matemáticas, sustituimos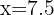 
en la ecuación de regresión y obtenemos
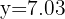
Un conjunto de datos bidimensionales 
tiene coeficiente de correlación 
, siendo las medias de las distribuciones marginales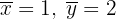 
. Se sabe que una de las cuatro ecuaciones siguientes corresponde a la recta de regresión de 
sobre 
:
1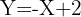
2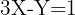
3
4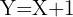
Seleccionar razonadamente esta recta.
Como el coeficiente de correlación lineal es negativo, la pendiente de la recta también será negativa, por tanto descartamos 
y
Un punto de la recta ha de ser , es decir, 
. Sustituimos en 1 y 3 para ver cual satisface la igualdad
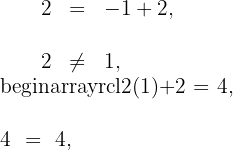
La recta pedida es 3.
Las estaturas y pesos de 
jugadores de baloncesto de un equipo son:
Estatura  | Pesos  | |
 |  | |
 | | |
 |  | |
 |  | |
 |  | |
|  |  |
 |  | |
 |  | |
 |  |
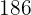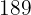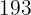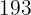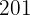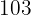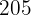Calcular:
1La recta de regresión de sobre 
.
2El coeficiente de correlación.
3El peso estimado de un jugador que mide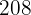 
cm.
|  | | | |
|---|---|---|---|---|
| |  |  |  |
| |  | |  |
| |  |  |  |
| |  |  |  |
| |  |  |  |
| | |  |  |
 | |  |  |  |
| |  |  |  |
| |  |  |  |
| |  |  |  |
 |  |  |  |  |
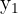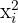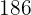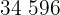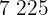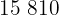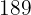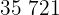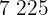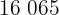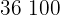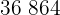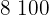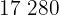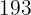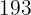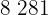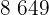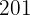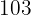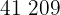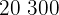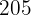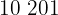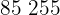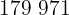Calculamos los promedios
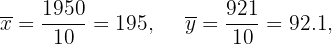
Calculamos la covarianza, las varianza y las desviaciones estándares
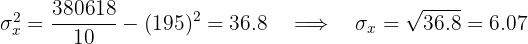
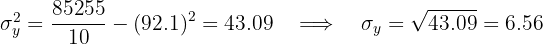
El coeficiente de correlación está dado por
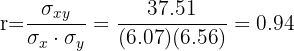
Se tiene una correlación positiva muy fuerte.
La recta de regresión de los pesos sobre las estaturas, es aquella que pasa por el punto y tiene pendiente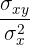 
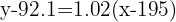
Despejamos y obtenemos la recta de regresión
Para encontrar el eso de un jugador que mide 208 cm, sustituimos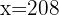 
en la ecuación de regresión y obtenemos
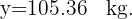
A partir de los siguientes datos referentes a horas trabajadas en un taller y las unidades producidas , determinar la recta de regresión de sobre , el coeficiente de correlación lineal e interpretarlo.
| Horas | Producción |
 |  |
 |  |
 |  |
 |  |
 | |
|  |
 | |
|  |
| |
| |
|  |
 |  |
| | | | |
|---|---|---|---|---|
| |  |  |  |
| |  |  |  |
| |  |  |  |
| |  |  |  |
| |  | |  |
| |  |  |  |
| |  | |  |
| | |  |  |
| | | |  |
| | | | |
| | |  |  |
| |  |  |  |
 |  |  |  |  |
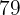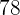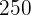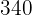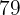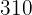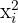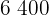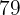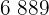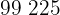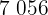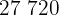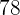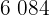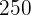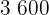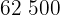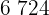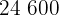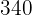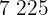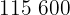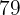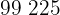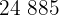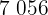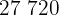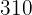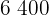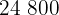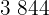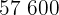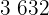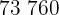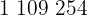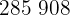Calculamos los promedios
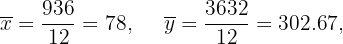
Calculamos la covarianza, las varianza y las desviaciones estándares
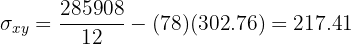
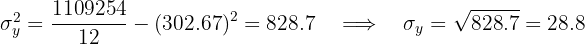
El coeficiente de correlación está dado por
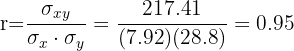
Se tiene una correlación positiva muy fuerte.
La recta de regresión de de sobre , es aquella que pasa por el punto y tiene pendiente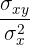
Despejamos y obtenemos la recta de regresión
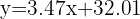
Se ha solicitado a un grupo de 
individuos información sobre el número de horas que dedican diariamente a dormir y ver la televisión. La clasificación de las respuestas ha permitido elaborar la siente tabla:
| Nº de horas dormidas | | | | | |
| Nº de horas de televisión | | | | | |
Frecuencias absolutas  | | | | | |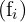
Se pide:
1Calcular el coeficiente de correlación.
2Determinar la ecuación de la recta de regresión de sobre .
3Si una persona duerme ocho horas y media, ¿cuánto cabe esperar que vea la televisión?
| |  |  |  |  |  |  |
|---|---|---|---|---|---|---|---|
| | | |  |  |  |  |
| | |  |  | |  |  |
| | | |  | |  |  |
| | | |  | | | |
| | | | | | | |
|  |  |  |  |  |
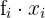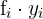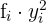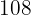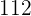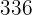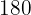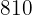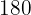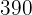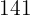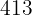Calculamos los promedios
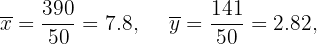
Calculamos la covarianza, las varianza y las desviaciones estándares
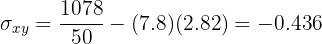
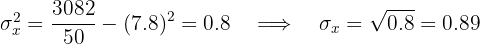
El coeficiente de correlación está dado por
Se tiene una correlación negativa y fuerte.
La recta de regresión de sobre , es aquella que pasa por el punto y tiene pendiente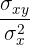
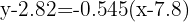
Despejamos y obtenemos la recta de regresión
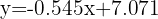
Para encontrar el número de horas que ve la televisión una persona que duerme ocho horas y media, sustituimos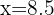 
en la ecuación de regresión y obtenemos
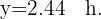
La tabla siguiente nos da las notas del test de aptitud dadas a seis dependientes a prueba y ventas del primer mes de prueba en cientos de euros.
| | |  |  |  | |
| | | | |  | |
1Hallar el coeficiente de correlación e interpretar el resultado obtenido.
2Calcular la recta de regresión de sobre .
3Predecir las ventas de un vendedor que obtenga 
en el test.
| | | | |
|---|---|---|---|---|
| | | |  |
| | |  |  |
| |  |  |  |
| |  | |  |
| |  |  |  |
| |  |  |  |
 |  |  |  |  |
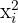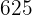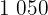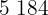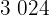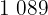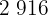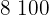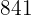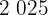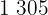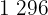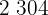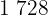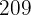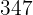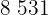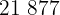Calculamos los promedios
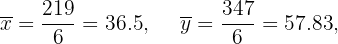
Calculamos la covarianza, las varianza y las desviaciones estándares
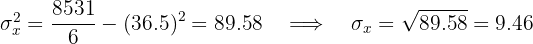
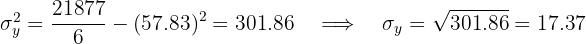
El coeficiente de correlación está dado por
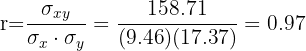
Se tiene una correlación positiva muy fuerte.
La recta de regresión de sobre , es aquella que pasa por el punto y tiene pendiente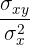
Despejamos y obtenemos la recta de regresión
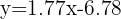
Para predecir las ventas de un vendedor que obtenga 47 en el test, sustituimos 
en la ecuación de regresión y obtenemos
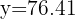
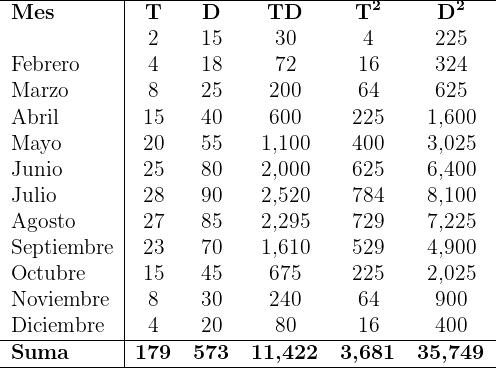
La siguiente tabla muestra la relación que hay entre la temperatura promedio mensual (T) en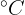 
de una ciudad en particular, y la venta de helado mensual en miles de dólares (D).
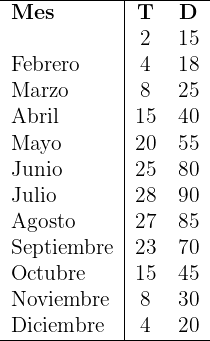
1Encontrar la recta de regresión de las ventas mensuales respecto a la temperatura promedio de cada mes.
2Calcular el coeficiente de correlación lineal e interpreta el resultado.
3A partir de la recta de regresión, ¿cuántos miles de dólares se venderían en un mes con una temperatura promedio de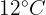 
?
4 Según esta misma línea, ¿tendría sentido para un puesto local de helados invertir 5 mil dólares en un mes cuya temperatura media es de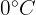 
?
1)
Queremos encontrar números reales 
y 
tal que podamos escribir 
se aproxime lo mejor posible a la recta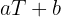 
. Primero, calculamos la suma de los datos 
y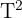 
.
Ahora calculamos los promedios, la covarianza, y las desviaciones estándar:
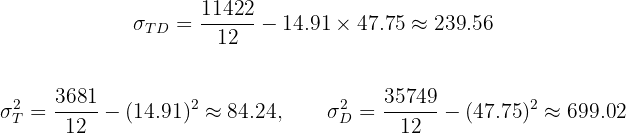
Es decir,
Por lo tanto, concluimos que
2) El coeficiente de correlación lineal estáa dado por
Es decir, la venta mensual de helados tiene una correlación fuerte positiva con la temperatura media de cada mes.
3)Queremos despejar para en la ecuación
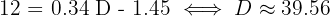
Entonces,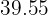 
es el valor que nuestra l\'inea de regresión espera en un mes cuya temperatura promedio es .
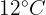4)Según nuestra recta de regresión, la venta de helados en un mes con esta temperatura sería de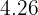 
mil dólares. Es decir, una inversión de mayor cantidad a ésta resulta en una pérdida de ganancia. Por lo tanto, al puesto no le conviene invertir esos 5 mil dólares.
La siguiente tabla muestra la relación entre el nivel máximo de estudios de un individuo y la probabilidad que tiene de estar en un rango de ingresos anuales (en miles de dólares)
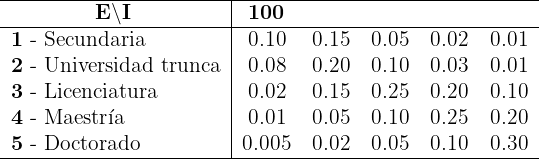
1Calcula la covarianza, la desviación estándar, y los promedios.
2Calcula el coeficiente de correlación.
1)
Convertimos la tabla dada a una simple. Representaremos al rang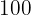o 
como y los demáss rangos serán representados con el promedio de los puntos límite.
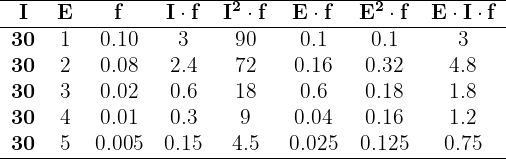
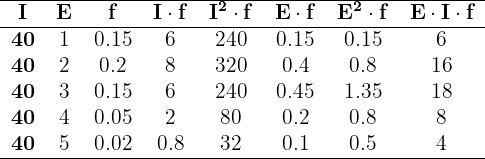
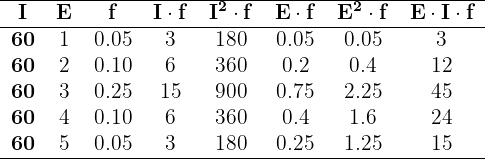
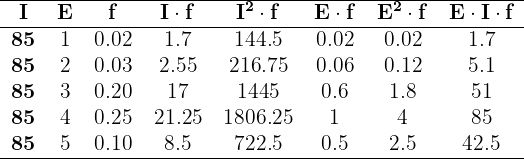
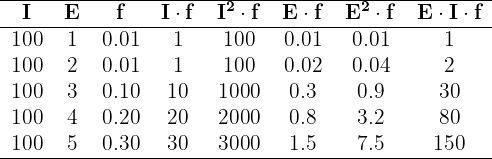
Sumando todas los valores de las columnas necesarias, tenemos
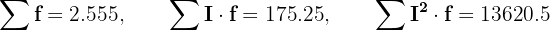
Además, tenemos
y la covarianza es
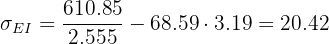
2)
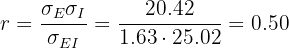
Es decir, hay una correlación moderada.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
En el cuarto ejercicio todas las ecuaciones concuerda, menos la primera ecuación, entonce cómo sabe que la tercera es la que pide
hola se menciona que «Como el coeficiente de correlación lineal es negativo, la pendiente de la recta también será negativa, por tanto se descarta ecuación 2 y 4» pues sus pendientes son 3 y 1, mientras la ecuación 3 si cumple pues su pendiente es -2.
Muchas gracias por la clara explicación de los 12 alumnos. Para mi, tienes 5 estrellas
solo que no he sabido despejar el polinomio
y – 5 = (5.92 / 6) * (x – 6) >>> y = 0.987 * x – 0.922
Para hallar la intercepción (-0.922) se me ha ocurrido que
como la recta siempre tiene que pasar exactamente por el punto de las medias
y como ya sabemos la media de y (5) y el coeficiente de x (0.987)
me basta con aplicarle el coeficiente a la media de x
y sacar la diferencia a la media de y.
intercepción = 5 – (0.987 * 6) = -0.922
Muy bien, otra manera es hacer x=0 y encontrar el valor de y.
En el ejercicio 1 la ecuación de la recta es: x=0,192 y-0,84
Ya revise el ejercicio y la ecuación es y=0.53x+302.91
Quisiera saber de donde sale el 0.53 del primer ejercicio
De dividir 22.8/42.58 o σy/σx.
Cuando se trata de establecer la correlación del peso de los hijos mayores con el peso del padre, cual coeficiente de correlación es más adecuado utilizarse