Name: Ejercicios de correlacion y regresion
Brand: Superprof
SKU: SP-RB-00013827
Rating: 4.22 (23 reviews)

1 Una compañía desea hacer predicciones del valor anual de sus ventas totales en cierto país a partir de la relación de éstas y la renta nacional. Para investigar la relación cuenta con los siguientes datos:

$\begin{matrix} \hline \textup{X} & \textup{Y}\\ \hline 189 & 402 \\ 190 & 404 \\ 208 & 412 \\ 227 & 425 \\ 239 & 429 \\ 252 & 436 \\ 257 & 440 \\ 274 & 447 \\ 293 & 458 \\ 308 & 469 \\ 316 & 469 \\ \hline \end{matrix}$

X representa la renta nacional en millones de euros e Y representa las ventas de la compañía en miles de euros en el periodo que va desde $1990$ hasta $2000$ (ambos inclusive). Calcular:

1 La recta de regresión de Y sobre X.

2 El coeficiente de correlación lineal e interpretarlo.

3 Si en $2001$ la renta nacional del país fue de $325$ millones de euros. ¿Cuál será la predicción para las ventas de la compañía en este año?

Una compañía desea hacer predicciones del valor anual de sus ventas totales en cierto país a partir de la relación de éstas y la renta nacional. Para investigar la relación cuenta con los siguientes datos:

X representa la renta nacional en millones de euros e Y representa las ventas de la compañía en miles de euros en el periodo que va desde $1990$ hasta $2000$ (ambos inclusive). Calcular:

1 La recta de regresión de Y sobre X.

$\begin{matrix} \hline & \textup{X}_{i} & \textup{Y}_{i} & \textup{X}_{i}^{2} & \textup{Y}_{i}^{2} & \textup{X}_{i}\cdot \textup{Y}_{i}\\ \hline & 189 & 402 & 35721 & 161604 & 75978\\ & 190 & 404 & 36100 & 163216 & 76760\\ & 208 & 412 & 43264 & 169744 & 85696\\ & 227 & 425 & 51529 & 180625 & 96475\\ & 239 & 429 & 57121 & 184041 & 102531\\ & 252 & 436 & 63504 & 190096 & 109872\\ & 257 & 440 & 66049 & 193600 & 113080\\ & 274 & 447 & 75076 & 199809 & 122478\\ & 293 & 458 & 85849 & 209764 & 134194\\ & 308 & 469 & 94864 & 219961 & 144452\\ & 316 & 469 & 99856 & 219961 & 148204\\ \sum & 2753 & 4791 & 708933 & 2092421 & 1209720 \\ \hline \end{matrix}$

$\bar{x}=\cfrac{2753}{11}=250.27$

$\bar{y}=\cfrac{4791}{11}=435.55$

$\sigma _{x}^{2}=\cfrac{708933}{11}-250.27^{2}=1813.38$

$\sigma _{y}^{2}=\cfrac{2092421}{11}-435.55^{2}=520.24$

$\sigma _{x}=\sqrt{1813.38}=42.58$

$\sigma _{y}=\sqrt{520.24}=22.8$

$\sigma _{xy}=\cfrac{1209720}{11}-250.27\cdot 435.55=969.44$

$y-435.55=0.53(x-250.27)\; \; \; \; \; \Rightarrow \; \; \; \; \; y=0.53+302.91$

2 El coeficiente de correlación lineal e interpretarlo.

$r=\cfrac{969.44}{42.58\cdot 22.8}=0.998$

Es un coeficiente de correlación positivo y cercano a uno, por lo que la correlación es directa y fuerte.

3 Si en 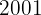$2001$ la renta nacional del país fue de $325$ millones de euros. ¿Cuál será la predicción para las ventas de la compañía en este año?

$y=0.53\cdot 325+302.91=475.16$

2 La información estadística obtenida de una muestra de tamaño 12 sobre la relación existente entre la inversión realizada y el rendimiento obtenido en cientos de miles de euros para explotaciones agrícolas, se muestra en el siguiente cuadro: Inversión (X), Rendimiento (Y)

$\begin{matrix} \hline \textup{X} & \textup{Y}\\ \hline 11 & 2\\ 14 & 3\\ 16 & 5\\ 15 & 6\\ 16 & 5\\ 18 & 3\\ 20 & 7\\ 21 & 10\\ 14 & 6\\ 20 & 10\\ 19 & 5\\ 11 & 6\\ \hline \end{matrix}$

Calcular:

1 La recta de regresión del rendimiento respecto de la inversión.

2 La previsión de inversión que se obtendrá con un rendimiento de 1 250 000 €.

La información estadística obtenida de una muestra de tamaño 12 sobre la relación existente entre la inversión realizada y el rendimiento obtenido en cientos de miles de euros para explotaciones agrícolas, se muestra en el siguiente cuadro:

$\begin{matrix} \hline \textup{X} & \textup{Y}\\ \hline 11 & 2\\ 14 & 3\\ 16 & 5\\ 15 & 6\\ 16 & 5\\ 18 & 3\\ 20 & 7\\ 21 & 10\\ 14 & 6\\ 20 & 10\\ 19 & 5\\ 11 & 6\\ \hline \end{matrix}$

Calcular:

1 La recta de regresión del rendimiento respecto de la inversión.

$\begin{matrix} \hline &\textup{X}_{i} & \textup{Y}_{i} & \textup{X}^{2}_{i} & \textup{Y}^{2}_{i} & \textup{X}_{i}^{2}\cdot \textup{Y}_{i}^{2}\\ \hline &11 & 2 & 121 & 4 & 22\\ &14 & 3 & 196 & 9 & 42\\ &16 & 5 & 256 & 25 & 80\\ &15 & 6 & 225 & 36 & 90\\ &16 & 5 & 256 & 25 & 80\\ &18 & 3 & 324 & 9 & 54\\ &20 & 7 & 400 & 49 & 140\\ &21 & 10 & 441 & 100 & 210\\ &14 & 6 & 196 & 36 & 84\\ &20 & 10 & 400 & 100 & 200\\ &19 & 5 & 361 & 25 & 95\\ &11 & 6 & 121 & 36 & 66\\ \sum & 195 & 68 & 3297 & 454 & 1163\\\hline \end{matrix}$

$\sigma _{x}^{2}=\cfrac{3297}{12}-16.25^{2}=10.96$

$\sigma _{y}^{2}=\cfrac{454}{12}-5.67^{2}=5.68$

$\sigma _{xy}=\cfrac{1163}{12}-16.25\cdot 5.67=4.78$

$y-7.75=\cfrac{4.78}{10.96}\, (x-16.25)\; \; \; \; \; \Rightarrow \; \; \; \; \; y=0.45x-1.64$

2 La previsión de inversión que se obtendrá con un rendimiento de 1 250 000 €.

$x-16.25=\cfrac{4.78}{5.68}\, (y-5.67)\; \; \; \; \; \Rightarrow \; \; \; \; \; x=0.84y+11.47$

$x=0.84\cdot 12.5+11.47=21.97$

$21.97\cdot 100000=2197000$

3 El número de horas dedicadas al estudio de una asignatura y la calificación obtenida en el examen correspondiente, de ocho personas es: Horas (X)Calificación (Y)

$\begin{matrix} \hline \textup{X} & \textup{Y}\\ \hline 20 & 6.5 \\ 16 & 6 \\ 34 & 8.5 \\ 23 & 7 \\ 27 & 9 \\ 32 & 9.5 \\ 18 & 7.5 \\ 22 & 8 \\ \hline \end{matrix}$

Se pide:

1 Recta de regresión de Y sobre X.

2 Calificación estimada para una persona que hubiese estudiado $28$ horas.

El número de horas dedicadas al estudio de una asignatura y la calificación obtenida en el examen correspondiente, de ocho personas es:

$\begin{matrix} \hline \textup{X} & \textup{Y}\\ \hline 20 & 6.5 \\ 16 & 6 \\ 34 & 8.5 \\ 23 & 7 \\ 27 & 9 \\ 32 & 9.5 \\ 18 & 7.5 \\ 22 & 8 \\ \hline \end{matrix}$

Se pide:

1 Recta de regresión de Y sobre X.

$\begin{matrix} \hline & \textup{X}_{i} & \textup{Y}_{i} & \textup{X}_{i}^{2} & \textup{Y}_{i}^{2} & \textup{X}_{i}\cdot \textup{Y}_{i} \\ \hline &20 & 6.5 & 256 & 36 & 96 \\ & 16 & 6 & 324 & 56.25 & 135 \\ &34 & 8.5 & 400 & 42.25 & 130 \\ &23 & 7 & 484 & 64 & 176 \\ &27 & 9 & 529 & 49 & 161 \\ &32 & 9.5 & 729 & 81 & 243 \\ &18 & 7.5 & 1024 & 90.25 & 304 \\ &22 & 8 & 1156 & 72.25 & 289 \\ \sum & 192 & 62 & 4902 & 491 & 1534 \\ \hline \end{matrix}$ ]

$\bar{x}=\cfrac{192}{8}=24$ $\bar{y}=\cfrac{62}{8}=7.75$

$\sigma ^{2}=\cfrac{4902}{8}-24^{2}=36.75$

$\sigma_{xy}=\cfrac{1534}{8}-24\cdot 7.75=5.75$

$y-7.75=\cfrac{5.75}{3.75}\, (x-24)$

$y=0.156x+4.006$

2 Calificación estimada para una persona que hubiese estudiado $28$ horas.

$y=0.156\cdot 28+4.006=8.4$

4 En la tabla siguiente se indica la edad (en años) y la conducta agresiva (medida en una escala de cero a 10) de 10 niños. EdadConducta Agresiva

$\begin{matrix} \hline \textup{Edad} & \textup{Conducta agresiva} \\ \hline 6 & 9\\ 6 & 6\\ 6.7 & 7\\ 7 & 8\\ 7.4 & 7\\ 7.9 & 4\\ 8 & 2\\ 8.2 & 3\\ 8.5 & 2\\ 8.9 & 1\\ \hline \end{matrix}$

1 Obtener la recta de regresión de la conducta agresiva en función de la edad.

2 A partir de dicha recta, obtener el valor de la conducta agresiva que correspondería a un niño de $7.2$ años.

En la tabla siguiente se indica la edad (en años) y la conducta agresiva (medida en una escala de cero a 10) de 10 niños.

$\begin{matrix} \hline \textup{Edad} & \textup{Conducta agresiva} \\ \hline 6 & 9\\ 6 & 6\\ 6.7 & 7\\ 7 & 8\\ 7.4 & 7\\ 7.9 & 4\\ 8 & 2\\ 8.2 & 3\\ 8.5 & 2\\ 8.9 & 1\\ \hline \end{matrix}$

1 Obtener la recta de regresión de la conducta agresiva en función de la edad.

$\begin{matrix} \hline & \textup{X}_{i} & \textup{Y}_{i} & \textup{X}_{i}^{2}& \textup{Y}_{i}^{2} & \textup{X}_{i}\cdot \textup{Y}_{i}\\ \hline &6 & 9 & 36 & 81 & 54\\ &6 & 6 & 40.96 & 36 & 38.4\\ &6.7 & 7 & 44.89 & 49 & 46.9\\ &7 & 8 & 49 & 64 & 56\\ &7.4 & 7 & 54.76 & 49 & 51.8\\ &7.9 & 4 & 62.41 & 16 & 31.6\\ &8 & 2 & 64 & 4 & 16\\ &8.2 & 3 & 67.24 & 9 & 24.6\\ &8.5 & 2 & 72.25 & 4 & 17\\ &8.9 & 1 & 79.21 & 1 & 8.9\\ \sum & 75 & 49 & 570.72 & 313 & 345.2\\ \hline \end{matrix}$

$\bar{x}=\cfrac{75}{10}=7.5$ $\bar{y}=\cfrac{49}{10}=4.9$

$\sigma _{x}^{2}=\cfrac{570.72}{10}-7.5^{2}=0.82$ $\sigma _{y}^{2}=\cfrac{313}{10}-4.9^{2}=7.29$

$\sigma _{xy}=\cfrac{345.2}{10}-7.5=-2.23$

$y-4.9=-2.72(x-7.5)\; \; \; \; \; \Rightarrow \; \; \; \; \; y=-2.72x+25.3$

2 A partir de dicha recta, obtener el valor de la conducta agresiva que correspondería a un niño de 7.2 años.

$y=-2.72\cdot 7.2+25.3=5.72$

5 Los valores de dos variables X e Y se distribuyen según la tabla siguiente:

$\begin{matrix} Y/X & 100 & 50 & 25\\ 14 & 1 & 1 & 0\\ 18 & 2 & 3 & 0\\ 22 & 0 & 1 & 2 \end{matrix}$

Se pide:

1 Calcular la covarianza.

2Obtener e interpretar el coeficiente de correlación lineal.

3Ecuación de la recta de regresión de Y sobre X.

Los valores de dos variables X e Y se distribuyen según la tabla siguiente:

$\begin{matrix} Y/X & 100 & 50 & 25\\ 14 & 1 & 1 & 0\\ 18 & 2 & 3 & 0\\ 22 & 0 & 1 & 2 \end{matrix}$

Se pide:

1 Calcular la covarianza.

Convertimos la tabla de doble entrada en una tabla simple.

$\begin{matrix} \hline & \textup{x}_{i} & \textup{y}_{i} & \textup{f}_{i} & \textup{x}_{i}\cdot \textup{f}_{i} & \textup{x}_{i}^{2}\cdot \textup{f}_{i} & \textup{y}_{i}\cdot \textup{f}_{i} & \textup{y}_{i}^{2}\cdot \textup{f}_{i} & \textup{x}_{i}\cdot \textup{y}_{i}\cdot \textup{f}_{i}\\ \hline & 100 & 14 & 1 & 100 & 10000 & 14 & 196 & 1400 \\ & 100 & 18 & 2 & 200 & 20000 & 36 & 648 & 3600 \\ & 50 & 14 & 1 & 50 & 2500 & 14 & 196 & 700 \\ & 50 & 18 & 3 & 150 & 7500 & 54 & 972 & 2700 \\ & 50 & 22 & 1 & 50 & 2500 & 22 & 484 & 1100 \\ & 25 & 22 & 2 & 50 & 1250 & 44 & 968 & 1100 \\ \hline \sum & & & 10 & 600 & 43750 & 184 & 3464 & 10600\\ \hline \end{matrix}$

$\bar{x}=\cfrac{600}{10}=60$ $\bar{y}=\cfrac{184}{10}=18.4$

$\sigma _{x}^{2}=\cfrac{43750}{10}-60^{2}=775$ $\sigma _{y}^{2}=\cfrac{3464}{10}-18.4^{2}=7.84$

$\sigma _{x}=\sqrt{775}=27.84$ $\sigma _{y}=\sqrt{7.84}=2.8$

$\sigma _{xy}=\cfrac{10600}{10}-60\cdot 18.4=-44$

2 Obtener e interpretar el coeficiente de correlación lineal.

$r=\cfrac{-44}{27.84\cdot 2.8}=-0.56$

Es una correlación negativa débil.

3 Ecuación de la recta de regresión de Y sobre X.

$y-18.4=-0.06(x-60)\; \; \; \; \; \Rightarrow \; \; \; \; \; y=-0.06x+22$

6 Las puntuaciones obtenidas por un grupo de alumnos en una batería de test que mide la habilidad verbal (X) y el razonamiento abstracto (Y) son las siguientes:

$\begin{matrix} 22> Y/X & 22> 20 & 22> 30 & 22> 40 & 22> 50\\ 22> (25-35) & 6 & 4 & 0 & 0\\ 22> (35-45) & 3 & 6 & 1 & 0\\ 22> (45-55) & 0 & 2 & 5 & 3\\ 22> (55-65) & 0 & 1 & 2 & 7 \end{matrix}$

Se pide:

1¿Existe correlación entre ambas variables?

2Según los datos de la tabla, si uno de estos alumnos obtiene una puntuación de $70$ puntos en razonamiento abstracto, ¿en cuánto se estimará su habilidad verbal?

Las puntuaciones obtenidas por un grupo de alumnos en una batería de test que mide la habilidad verbal (X) y el razonamiento abstracto (Y) son las siguientes:

$\begin{matrix} 22> Y/X & 22> 20 & 22> 30 & 22> 40 & 22> 50\\ 22> (25-35) & 6 & 4 & 0 & 0\\ 22> (35-45) & 3 & 6 & 1 & 0\\ 22> (45-55) & 0 & 2 & 5 & 3\\ 22> (55-65) & 0 & 1 & 2 & 7 \end{matrix}$

Se pide:

1 ¿Existe correlación entre ambas variables?

Convertimos la tabla de doble entrada en tabla simple.

$\begin{matrix} \hline & \textup{x}_{i} & \textup{y}_{i} & \textup{f}_{i} & \textup{x}_{i}\cdot \textup{f}_{i} & \textup{x}_{i}^{2}\cdot \textup{f}_{i} & \textup{y}_{i}\cdot \textup{f}_{i} & \textup{y}_{i}^{2}\cdot \textup{f}_{i} & \textup{x}_{i}\cdot \textup{y}_{i}\cdot \textup{f}_{i}\\ \hline & 20 & 30 & 6 & 120 & 2400 & 180 & 5400 & 3600\\ & 20 & 40 & 3 & 60 & 1200 & 120 & 4800 & 2400\\ & 30 & 30 & 4 & 120 & 3600 & 120 & 3600 & 3600\\ & 30 & 40 & 6 & 180 & 5400 & 240 & 9600 & 7200\\ & 30 & 50 & 2 & 60 & 1800 & 100 & 5000 & 3000\\ & 30 & 60 & 1 & 30 & 900 & 60 & 3600 & 1800\\ & 40 & 40 & 1 & 40 & 1600 & 40 & 1600 & 1600\\ & 40 & 50 & 5 & 200 & 8000 & 250 & 12500 & 10000\\ & 40 & 60 & 2 & 80 & 3200 & 120 & 7200 & 4800\\ & 50 & 50 & 3 & 150 & 7500 & 150 & 7500 & 7500\\ & 50 & 60 & 7 & 350 & 17500 & 420 & 25200 & 21000\\ \hline \sum & & & 40 & 1390 & 53100 & 1080 & 86000 & 66500\\ \hline \end{matrix}$

$\bar{x}=\cfrac{1390}{40}=34.75$ $\bar{y}=\cfrac{1800}{40}=45$

$\sigma _{x}^{2}=\cfrac{53100}{40}-34.75^{2}=119.94$ $\sigma _{y}^{2}=\cfrac{86000}{40}-45^{2}=125$

$\sigma _{x}=\sqrt{119.94}=10.95$ $\sigma _{y}=\sqrt{125}=11.18$

$\sigma _{xy}=\cfrac{66500}{40}-34.75\cdot 45=98.75$

$r=\cfrac{98.75}{10.95\cdot 11.18}=0.81$

Existe una correlación positiva fuerte

2 Según los datos de la tabla, si uno de estos alumnos obtiene una puntuación de $70$ puntos en razonamiento abstracto, ¿en cuánto se estimará su habilidad verbal?

$x-34.75=\cfrac{98.75}{125}\, (y-45)\; \; \; \; \; \Rightarrow \: \: \: \: \: x=0.79y-0.8$

$x=0.79\cdot 70-0.8=54.5$

7 Se sabe que entre el consumo de papel y el número de litros de agua por metro cuadrado que se recogen en una ciudad no existe relación.

1¿Cuál es el valor de la covarianza de estas variables?

2¿Cuánto vale el coeficiente de correlación lineal?

3¿Qué ecuaciones tienen las dos rectas de regresión y cuál es su posición en el plano?

Se sabe que entre el consumo de papel y el número de litros de agua por metro cuadrado que se recogen en una ciudad no existe relación.

1 ¿Cuál es el valor de la covarianza de estas variables?

$\sigma _{xy}=0$

2 ¿Cuánto vale el coeficiente de correlación lineal?

$r=0$

3 ¿Qué ecuaciones tienen las dos rectas de regresión y cuál es su posición en el plano?

$\bar{x}=k_{1},\bar{y}=k_{2}\; \; \; \; \; \; \; \; \; \; k_{1},k_{2}\; \epsilon\; \mathbb{R}^{+}$

Las rectas son paralelas a los ejes y perpendiculares entre sí.

8 En una empresa de transportes trabajan cuatro conductores. Los años de antigüedad de permisos de conducir y el número de infracciones cometidas en el último año por cada uno de ellos son los siguientes:

$\begin{matrix} \hline \textup{A\~{n}os (X)} & 3 & 4 & 5 & 6 \\ \hline \textup{Infracciones (Y)} & 4 & 3 & 2 & 1\\ \hline \end{matrix}$

Calcular el coeficiente de correlación lineal e interpretarlo.

En una empresa de transportes trabajan cuatro conductores. Los años de antigüedad de permisos de conducir y el número de infracciones cometidas en el último año por cada uno de ellos son los siguientes:

$\begin{matrix} \hline \textup{A\~{n}os (X)} & 3 & 4 & 5 & 6 \\ \hline \textup{Infracciones (Y)} & 4 & 3 & 2 & 1\\ \hline \end{matrix}$

Calcular el coeficiente de correlación lineal e interpretarlo.

$\begin{matrix} \hline & \textup{x}_{i} & \textup{y}_{i} & \textup{x}_{i}\cdot \textup{y}_{i} & \textup{x}_{i}^{2} & \textup{y}_{i}^{2} \\ \hline & 3 & 4 & 12 & 9 & 16\\ & 4 & 3 & 12 & 16 & 9\\ & 5 & 2 & 10 & 25 & 4\\ & 6 & 1 & 6 & 36 & 1\\ \hline \sum & 18 & 10 & 40 & 86 & 30\\ \hline \end{matrix}$

$\bar{x}=\cfrac{18}{4}=4.5$ $\bar{y}=\cfrac{10}{4}=2.5$

$\sigma _{x}^{2}=\cfrac{86}{4}-4.5^{2}=1.25$ $\sigma _{y}^{2}=\cfrac{30}{4}-2.5^{2}=1.25$

$\sigma _{xy}=\cfrac{40}{4}-4.5\cdot 2.5=-1.25$

$r=\cfrac{-1.25}{\sqrt{1.25}\cdot \sqrt{1.25}}=\cfrac{-1.25}{1.25}=-1$

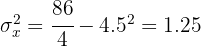
La correlación es perfecta e inversa.

9 Una persona rellena semanalmente una quiniela y un boleto de lotería primitiva anotando el número de aciertos que tiene. Durante las cuatro semanas del mes de febrero, los aciertos fueron:

$\begin{matrix} \textup{Quiniela (X)} & 6 & 8 & 6 & 8\\ \textup{Primitiva (Y)} & 1 & 2 & 2 & 1 \end{matrix}$

Obtener el coeficiente de correlación lineal e interpretarlo. ¿Ofrecerían confianza las previsiones hechas con las rectas de regresión?

Una persona rellena semanalmente una quiniela y un boleto de lotería primitiva anotando el número de aciertos que tiene. Durante las cuatro semanas del mes de febrero, los aciertos fueron:

$\begin{matrix} \textup{Quiniela (X)} & 6 & 8 & 6 & 8\\ \textup{Primitiva (Y)} & 1 & 2 & 2 & 1 \end{matrix}$

Obtener el coeficiente de correlación lineal e interpretarlo. ¿Ofrecerían confianza las previsiones hechas con las rectas de regresión?

$\begin{matrix} \hline & \textup{x}_{i} & \textup{y}_{i} & \textup{x}_{i}\cdot \textup{y}_{i} & \textup{x}_{i}^{2} & \textup{y}_{i}^{2}\\ \hline & 6 & 1 & 6 & 36 & 1\\ & 8 & 2 & 16 & 64 & 4\\ & 6 & 2 & 12 & 36 & 4\\ & 8 & 1 & 8 & 64 & 1\\ \hline \sum & 28 & 6 & 42 & 200 & 10 \\ \hline \end{matrix}$

$\bar{x}=\cfrac{28}{4}=7$ $\bar{y}=\cfrac{6}{4}=1.5$

$\sigma _{x}^{2}=\cfrac{200}{4}-7^{2}=1$ $\sigma _{y}^{2}=\cfrac{10}{4}-1.5^{2}=0.25$

$\sigma _{x}=\sqrt{1}=1$ $\sigma _{y}=\sqrt{0.25}=0.5$

$\sigma _{xy}=\cfrac{42}{4}-7\cdot 1.5=0$

$r=\cfrac{0}{1\cdot 0.5}=0$

No existe correlación entre ambas variables, por tanto las estimaciones hechas con las rectas de regresión no ofrece ninguna confianza.

Si necesitas ayuda adicional, recurda que en Superprof podrás encontrar el curso matematicas perfecto para ti.

La plataforma que conecta profes particulares y estudiantes

¿Te ha gustado este artículo? ¡Califícalo!

4,22 (23 nota(s))

Cargando...

Marta

➗ Licenciada en Químicas da clase de Matemáticas, Física y Química -> Comparto aquí mi pasión por las matemáticas ➗

Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.

Déjanos un comentario

Cancelar la respuesta

James

Agosto 2022

En una muestra de 80 universitarios, Thalberg (1987) íntercorrelacionó la inteligencia
(X), la velocidad de lectura (Y) y la comprensión de lectura (Z), encontrando los
siguientes coeficientes de correlación: rxy=−0.340, rxz=0.422 y ryz=−0.385. Con un nivel
de significación de 0.05, contrasta la hipótesis de que la inteligencia se correlaciona por
igual con la velocidad de lectura que con la comprensión.

leandro

Junio 2022

4.Desempeño de un automóvil. Se acopla un dinamómetro a un
motor de automóvil V8 y se mide su potencia en caballos y a
diferentes velocidades x (en miles de revoluciones por minuto).
En la siguiente tabla se muestran los resultados.
a) Utilizar las funciones de cálculo de regresión de una herramienta
de graficación para encontrar el modelo cúbico
para los datos.
b) Utilizar la herramienta de graficación para representar los
datos y el modelo.
c) Utilizar el modelo para estimar la potencia cuando el motor
gira a 4 500 revoluciones por minuto.

charly

Abril 2022

Hola que tal me podrían ayudar con un trabajo de Favor?

Determinar si existe relación lineal entre el peso (x) y el volumen (y) de un envase cilíndrico mediante el coeficiente de Pearson:
r = (n ∑xy – ∑x ∑y) / [n ∑x2-∑x)2 [n∑y2-∑y2]

Peso Volumen
(grs.) (cm)
x y xy x2 y2
198 990
199 993
200 996
201 999
202 1,002
203 1,005
204 1,005
205 1,011
206 1,019
208 1,021
∑ 2026 10,041

John

Diciembre 2021

La tabla ilustra los puntos que obtuvieron en un examen y el tiempo en horas que dedicaron para prepararlo
Tiempo x Puntos y x∙y x^2
11 9 99
8 7 56
9 8 72
5 6 30
7 7 49
2 1 2

ROLANDO CASTILLO DURAND

Noviembre 2021

Excelentes ejercicios, muchas gracias, será de mucha ayuda para mis alumnos

Superprof

Diciembre 2021

🤗

Luis Antonio Sánchez Martínez

Noviembre 2021

Ayuda porfavor, Interprete cada uno de los siguientes coeficientes de correlación y use gráficos de
dispersión para representar como se vería cada una de las relaciones entre dos variables
(x, y) cualesquiera:

a) 𝑟 = −1.0 b) 𝑟 = 0.05 c) 𝑟 = 0.85

Emily

Noviembre 2021

En un estudio clínico se predice el peso de los niños en base a la edad que tienen. Se toma una muestra de cinco niños que tienen 2, 3, 4, 6 y 10 años, sus pesos son 14, 20, 30, 38 y 52 kilos respectivamente. ¿Cuáles son las variables dependiente e independiente? a) La variable dependiente es la edad y la independiente es la edad. b) La variable dependiente es el peso y la independiente es la edad. c) La variable dependiente es el peso y la independiente es el peso. d) La variable dependiente es la edad y la independiente es el peso de los niños?
Ayuda plis

Ejercicios de correlación y regresión

Distribuciones bidimensionales

Coeficiente de correlacion

Covarianza

¿Que es la recta de regresion?

Correlacion estadistica

Ejercicios de regresion y correlacion II

Cancelar la respuesta

Ejercicios de correlación y regresión

Teoría

Distribuciones bidimensionales

Coeficiente de correlacion

Covarianza

¿Que es la recta de regresion?

Correlacion estadistica

Otros ejercicios

Ejercicios de regresion y correlacion II

Cancelar la respuesta