Una variable aleatoria continua, X, sigue una distribución normal de media μ y desviación típica σ, y se designa por N(μ, σ), si se cumplen las siguientes condiciones:
1 La variable puede tomar cualquier valor: (-∞, +∞)
2 La función de densidad, que es la expresión matemática de la curva de Gauss o Campana de Gauss está dada por:
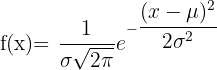
Propiedades
1 El campo de existencia o dominio es cualquier valor real, es decir, (-∞, +∞).
2 Es simétrica respecto a la media µ.
3 Tiene un máximo en la media µ.
4 Crece hasta la media µ y decrece a partir de ella.
5 En los puntos µ − σ y µ + σ presenta puntos de inflexión.
6 El eje de abscisas es una asíntota de la curva.
7 El área encerrada por la función y el eje de abscisas es igual a la unidad.
8Al ser simétrica respecto al eje que pasa por x = µ, deja un área igual a 0.5 a la izquierda y otra igual a 0.5 a la derecha.
9 La probabilidad equivale al área encerrada bajo la curva.
p(μ - σ < X ≤ μ + σ) = 0.6826 = 68.26 %
p(μ - 2σ < X ≤ μ + 2σ) = 0.954 = 95.4 %
p(μ - 3σ < X ≤ μ + 3σ) = 0.997 = 99.7 %
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
ERROR
En el apartado 1 del ejercicio 7 hay un error; si buscamos el 0.66 en la tabla, encontraremos que su resultado es 0,7454, no 0,7486, ya que ese es el número que nos da al buscar 0.67 en lugar del 0.66, que es el que tenemos que buscar.
Sucede lo mismo en el tercer apartado del mismo ejercicio; si buscamos 1.66 en la tabla, nos va a dar 0,9515 en lugar de 0,9525, ya que eso es lo que da si buscamos el número 1.67, no el 1.66.
Buenas tardes.
Hola, muchas gracias por tu observación y una disculpa por el error ya se corrigió.
Distribución normal para la Muestra.
Elige el tamaño de la muestra de 120 personas de una población distribuida normalmente, con una media poblacional de 80 y una desviación estándar de la población de 5.4772.
Selecciona la respuesta correcta de la probabilidad, para que la media de la muestra de lo siguiente:
P( X̅= 81).
Hola
Me pueden ayudar:
Dada una distribución normal con �=1000 y �=200, calcule las siguientes 10 probabilidades:
1.1 p(x ≤ 800)
1.2 p(x ≥ 1200)
1.3 p(800 ≤ x ≤ 1200)
2.1p(x ≤ 600)
2.2 p(x ≥ 1400)
2.3 p(600 ≤ x ≤ 1400)
3.1 p(x ≤ 400)
3.2 p(x ≥ 1600)
3.3 p(400 ≤ x ≤ 1600)
4. Si la p(x ≤ NÚMERO) = 4% , calcule ese número.
Hola! No comprendo de dónde salió el -0.67 de 0.25 en la tabla. Si pueden aclarar mis dudas agradezco de antemano.
Feliz día!
En la primera tabla ubica el valor 0.2514 en la octava columna y a la izquierda tienes -0.6 y hacia arriba es 0.07 lo que implica -0.67
Hola,La probabilidad de que la rentabilidad sea mayor a 0,33 con un promedio de 0,23 aplicando la distribución normal, con los siguientes datos es:
escenario probabilidad rentabilidad
optimista 0,25 0,26
normal 0,65 0,30
pesimista 0,10 – 0,35
a.30,10 %
b.29,81 %
c.28,85 %
d.29,15 %