Tabla de distribución normal
La tabla de distribución normal se utiliza para localizar valores definidos para la variable z.
Te podemos ayudar a encontrar las mejores clases de matematicas primaria para que entiendas todo desde el principio.
Ejercicios de distribución normal
Si 
es una variable aleatoria de una distribución 
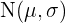, hallar: 
Si es una variable aleatoria de una distribución 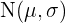, hallar: .
En este caso, se esta trabajando con una distribución normal estandar, para resolverlo utilizaremos la formula siguiente:
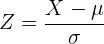
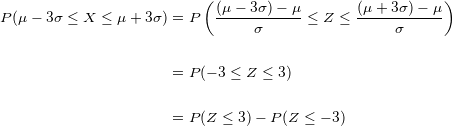
Ahora, tenemos que localizar en nuestra tabla de distribución normal, localizamos el valor cuando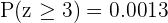 
, pero necesitamos el valor para cuando 
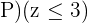, entonces se utiliza 
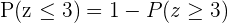entonces obtenemos que 
. Además, como la distribución normal es simétrica, tenemos que 
.
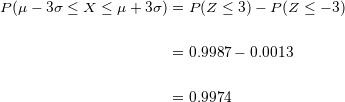
Es decir, que aproximadamente el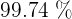 
de los valores de están a menos de tres desviaciones típicas de la media.
En una distribución normal de media 
y desviación típica 
, calcular el valor de a para que: 
En una distribución normal de media y desviación típica , calcular el valor de a para que:
Utilizando la formula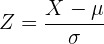 
, vamos a sustituir el valor de la media ( 
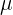), y la desviación típica ( 
).
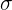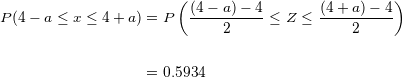
Al simplificar, obtenemos:
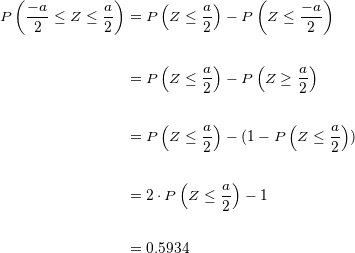
De donde se sigue que
Ahora localizamos en la tabla de distribución normal el valor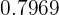 
y observamos que corresponde a 
, entonces:
En una ciudad se estima que la temperatura máxima en el mes de junio sigue una distribución normal, con media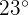 
y desviación típica 
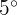. Calcular el número de días del mes en los que se espera alcanzar máximas entre 
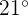y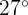 
.
En una ciudad se estima que la temperatura máxima en el mes de junio sigue una distribución normal, con media 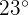y desviación típica .
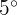Calcular el número de días del mes en los que se espera alcanzar máximas entre 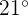y .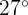
Utilizando la formula 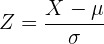, vamos a sustituir el valor de la media (
), y la desviación típica ( 
).
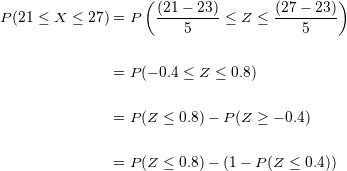
Buscamos los valores correspondientes en la tabla de distribución normal:
Por lo tanto
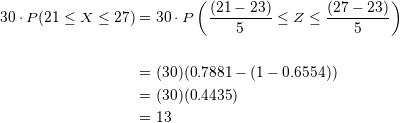
Esto quiere decir, que en todo el mes, solo 
días alcanzarán temperaturas entre 
y 
grados.
La media de los pesos de 
estudiantes de un colegio es 
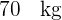y la desviación típica 
.
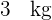Suponiendo que los pesos se distribuyen normalmente, hallar cuántos estudiantes pesan:
1 Entre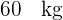 
y 
.
2 Más de 
.
3 Menos de 
.
4 .
5 o menos.
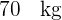La media de los pesos de estudiantes de un colegio es y la desviación típica .
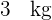Suponiendo que los pesos se distribuyen normalmente, hallar cuántos estudiantes pesan:
1 Entre 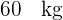y .
Sustituyendo:
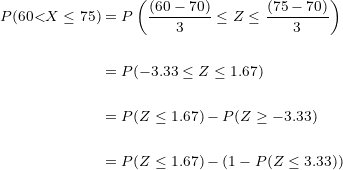
Localizando los valores en la tabla de distribución normal y operando:
Por lo tanto, si multiplicamos la probabilidad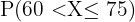 
por los estudiantes tenemos
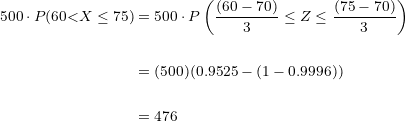
De los estudiantes 
se encuentran entre los 
y 
kilogramos de peso.
2 Más de .
Sustituyendo y simplificando tenemos:
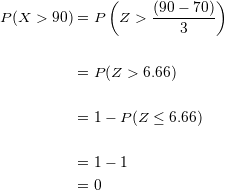
Multiplicando la probabilidad por obtenemos
.
Es imposible hallar a un solo estudiante por encima de los 
kilogramos.
3 Menos de .
Sustituyendo y simplificando tenemos:
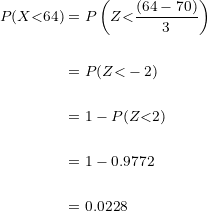
Multiplicando la probabilidad por obtenemos
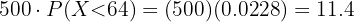
Hay 
estudiantes que pesan menos de 
kilogramos
4 .
Cuando la distribución es continua, la probabilidad de que la variable tenga un valor exacto siempre es nula (
). Por lo tanto
.
5 o menos.
Dados los resultados anteriores:
Existen cero estudiantes que pesan kilogramos exactos y hay estudiantes que pesan menos de kilogramos, entonces, existen estudiantes que pesan kilogramos o menos.
.
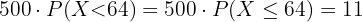Se supone que los resultados de un examen siguen una distribución normal con media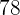 
y desviación típica 
. Se pide:
1 ¿Cuál es la probabilidad de que una persona que se presenta el examen obtenga una calificación superior a 
?
2 Calcular la proporción de estudiantes que tienen puntuaciones que exceden por lo menos en cinco puntos de la puntuación que marca la frontera entre el Apto y el No-Apto (son declarados No-Aptos el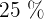 
de los estudiantes que obtuvieron las puntuaciones más bajas)
3 Si se sabe que la calificación de un estudiante es mayor que , ¿cuál es la probabilidad de que su calificación sea, de hecho, superior a 
?
Se supone que los resultados de un examen siguen una distribución normal con media 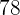y desviación típica .
Se pide:
1 ¿Cuál es la probabilidad de que una persona que se presenta el examen obtenga una calificación superior a ?
Sustituimos los valores en la formula:
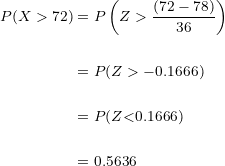
La probabilidad de que una persona obtenga una puntuación mayor a al presentar el examen es de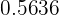 
.
2 Calcular la proporción de estudiantes que tienen puntuaciones que exceden por lo menos en cinco puntos de la puntuación que marca la frontera entre el Apto y el No-Apto (son declarados No-Aptos el 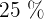de los estudiantes que obtuvieron las puntuaciones más bajas).
Sustitución de valores en la formula:
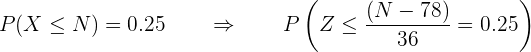
Localizamos la probabilidad 
en la tabla de distribución de normal, es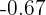 
, esto significa que
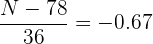
Despejamos 
:
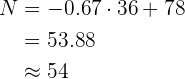
Calculamos para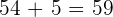 
:
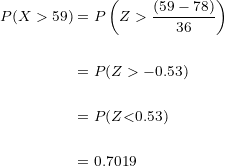
El porcentaje de alumnos que son Aptos y ademas su puntaje esta unidades por encima de la frontera de No-Aptos es de 
.
3 Si se sabe que la calificación de un estudiante es mayor que ¿Cuál es la probabilidad de que su calificación sea, de hecho, superior a ?
Sustituimos:
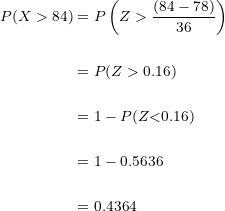
Por el primer inciso de este ejercicio sabemos que la probabilidad de que un alumno obtenga una puntuación mayor a los puntos al hacer el examen es de .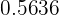
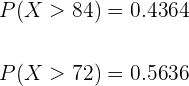
Ahora utilizaremos la formula de probabilidad condicional:
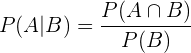
Sustituimos:
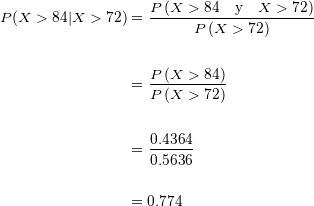
La probabilidad de que un alumno que obtuvo una puntuación mayor a haya obtenido de hecho una puntuación mayor a es de 
.
Tras un test de cultura general se observa que las puntuaciones obtenidas siguen una distribución una distribución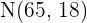 
. Se desea clasificar a los examinados en tres grupos (de baja cultura general, de cultura general aceptable, de excelente cultura general) de modo que hay en el primero un 
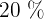la población, un 
el segundo y un 
en el tercero.
¿Cuáles han de ser las puntuaciones que marcan el paso de un grupo al otro?
Tras un test de cultura general se observa que las puntuaciones obtenidas siguen una distribución una distribución .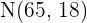
Se desea clasificar a los examinados en tres grupos (de baja cultura general, de cultura general aceptable, de excelente cultura general) de modo que hay en el primero un 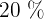la población, un el segundo y un en el tercero.
¿Cuáles han de ser las puntuaciones que marcan el paso de un grupo al otro?
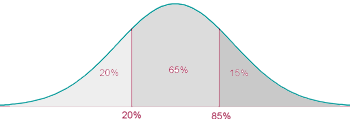
Localizamos en nuestra tabla el parámetro correspondiente a la probabilidad 
, el cual es 
:
Por lo que, si 
, entonces
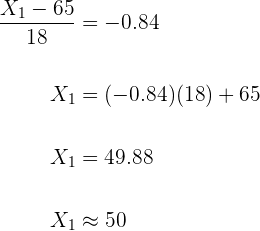
Ahora localizamos en la tabla el parámetro para la probabilidad de 
, el cual es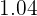 
, lo que significa que
Por lo que, si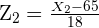 
, entonces
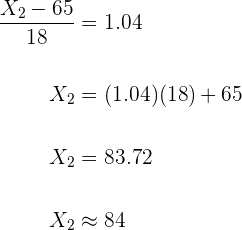
Baja cultura hasta 
puntos.
Cultura aceptable entre y .
Excelente cultura a partir de puntos.
Varios test de inteligencia dieron una puntuación que sigue una ley normal con media 
y desviación típica 
.
1 Determinar el porcentaje de población que obtendría un coeficiente entre 
y 
.
2 ¿Qué intervalo centrado en contiene al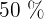 
de la población?
3 En una población de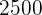 
individuos, ¿cuántos individuos se esperan que tengan un coeficiente superior a 
?
Varios test de inteligencia dieron una puntuación que sigue una ley normal con media y desviación típica .
1 Determinar el porcentaje de población que obtendría un coeficiente entre y .
Sustitución de valores en la formula:
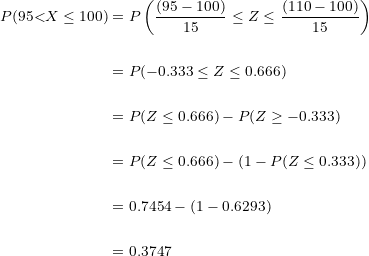
El porcentaje de la población que obtendrá un puntaje entre y es de 
.
2 ¿Qué intervalo centrado en contiene al 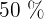de la población?
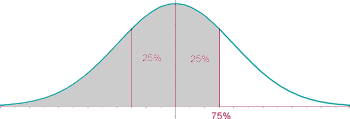
Como queremos tomar el 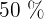del centro de la población, entonces tomamos el intervalo que esta entre 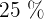el y el 
Localizamos en la tabla el parámetro para la probabilidad de 
y de
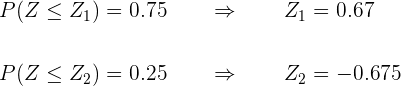
Sustituimos y despejamos
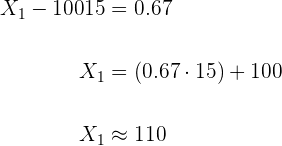
y
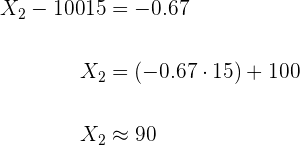
Entonces, el intervalo es: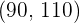 
.
El intervalo centrado que contiene al 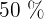de la población obtendrá un puntaje entre y .
3 En una población de 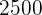individuos, ¿cuántos individuos se esperan que tengan un coeficiente superior a ?
Sustituimos valores en la formula, calculamos el parámetro y localizamos la probabilidad en la tabla
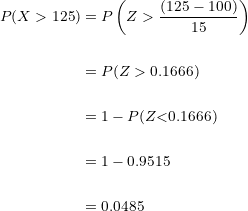
Multiplicando esta probabilidad por los 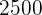individuos obtenemos
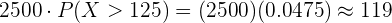
En una población de 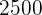individuos, se espera que 
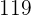de ellos tengan un coeficiente superior a .
En una ciudad una de cada tres familias posee teléfono. Si se eligen al azar familias, calcular la probabilidad de que entre ellas haya por lo menos 
con teléfono.
En una ciudad una de cada tres familias posee teléfono.
Si se eligen al azar familias, calcular la probabilidad de que entre ellas haya por lo menos con teléfono
-
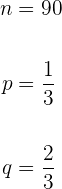
- n: Cantidad de familias a elegir.
- p: Probabilidad de seleccionar una familia que tenga teléfono.
- q: Complemento de la probabilidad.
Para resolver este tipo de ejercicios usaremos el Teorema de Moivre-Laplace para Probabilidad:.
Si tenemos que es una variable aleatoria binomial de parámetros 
y
, 
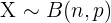, entonces se puede aproximar a una distribución normal de media 
y desviación típica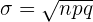 
(donde 
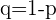) si se cumplen las dos condiciones siguientes:
-
-
-
- Condición 1.
. - Condición 2.
.
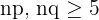- Condición 1.
-
-
Entonces, la variable binomial 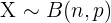quedaría aproximada por la variable normal 
.
Como 
, se cumple la condición 1.
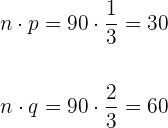
Entonces, se cumple la condición 2.
Entonces utilizamos la formula .
Sustituimos los datos:
Ahora utilizamos la formula de distribución normal
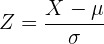
Sustituimos , operamos y localizamos el valor de la probabilidad en nuestra tabla de distribución normal:
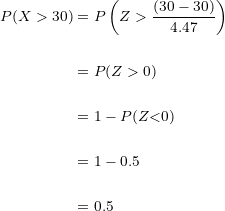
Al seleccionar familias al azar, existe una probabilidad de 
de haber seleccionado por lo menos familias con teléfono.
En un examen tipo test de 
preguntas de elección múltiple, cada pregunta tiene una respuesta correcta y una incorrecta. Se aprueba si se contesta a más de respuestas correctas. Suponiendo que se contesta al azar, calcular la probabilidad de aprobar el examen.
En un examen tipo test de preguntas de elección múltiple, cada pregunta tiene una respuesta correcta y una incorrecta.
Se aprueba si se contesta a más de respuestas correctas.
Suponiendo que se contesta al azar, calcular la probabilidad de aprobar el examen
Utilizamos el Teorema de Moivre-Laplace para Probabilidad:
Comprobamos las condiciones:
Primera condición:
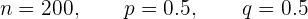
Como ambas condiciones se cumplen, usaremos la formula
.
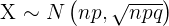Sustituimos:
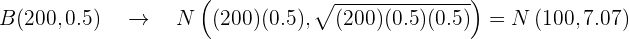
Ahora utilizaremos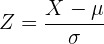
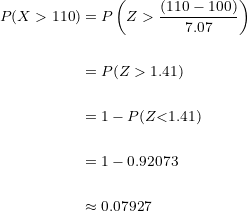
Al contestar al azar un examen tipo test de opción múltiple existe la probabilidad de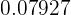 
de aprobar.
Un estudio ha mostrado que, en un cierto barrio, el 
de los hogares tienen al menos dos televisores, se elige al azar una muestra de hogares en el citado barrio. Se pide:
1 ¿Cuál es la probabilidad de que al menos 
de los citados hogares tengan cuando menos dos televisores?
2 ¿Cuál es la probabilidad de que entre 
y 
hogares tengan cuando menos dos televisores?
Un estudio ha mostrado que, en un cierto barrio, el de los hogares tienen al menos dos televisores Se elige al azar una muestra de hogares en el citado barrio.
Se pide:
1 ¿Cuál es la probabilidad de que al menos de los citados hogares tengan cuando menos dos televisores?
Utilizamos el Teorema de Moivre-Laplace para Probabilidad, comprobamos si se cumplen las condiciones:
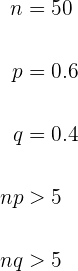
Como ambas condiciones se cumplen, usaremos la formula .
Sustituimos:
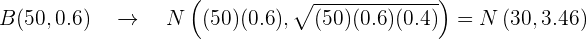
Ahora utilizaremos .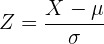
Sustituimos:
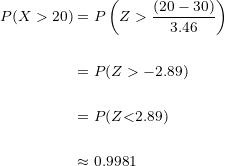
2 ¿Cuál es la probabilidad de que entre y hogares tengan cuando menos dos televisores?
Utilizando la formula 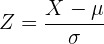, vamos a sustituir el valor de la media 
y la desviación típica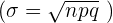 
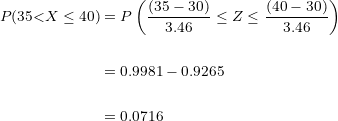
La probabilidad de que entre y hogares tengan al menos televisores es de 
.
¿Te pierdes y necesitas refuerzo? No te preocupes, en Superprof te ayudamos con las clases de matematicas secundaria.
Encuentra el mejor curso matematicas de todos los que te proponemos en Superprof. Podrás aprender tanto con un profesor de matematicas online como con uno presencial. ¡Tu decides!
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
ERROR
En el apartado 1 del ejercicio 7 hay un error; si buscamos el 0.66 en la tabla, encontraremos que su resultado es 0,7454, no 0,7486, ya que ese es el número que nos da al buscar 0.67 en lugar del 0.66, que es el que tenemos que buscar.
Sucede lo mismo en el tercer apartado del mismo ejercicio; si buscamos 1.66 en la tabla, nos va a dar 0,9515 en lugar de 0,9525, ya que eso es lo que da si buscamos el número 1.67, no el 1.66.
Buenas tardes.
Hola, muchas gracias por tu observación y una disculpa por el error ya se corrigió.
Distribución normal para la Muestra.
Elige el tamaño de la muestra de 120 personas de una población distribuida normalmente, con una media poblacional de 80 y una desviación estándar de la población de 5.4772.
Selecciona la respuesta correcta de la probabilidad, para que la media de la muestra de lo siguiente:
P( X̅= 81).
Hola
Me pueden ayudar:
Dada una distribución normal con �=1000 y �=200, calcule las siguientes 10 probabilidades:
1.1 p(x ≤ 800)
1.2 p(x ≥ 1200)
1.3 p(800 ≤ x ≤ 1200)
2.1p(x ≤ 600)
2.2 p(x ≥ 1400)
2.3 p(600 ≤ x ≤ 1400)
3.1 p(x ≤ 400)
3.2 p(x ≥ 1600)
3.3 p(400 ≤ x ≤ 1600)
4. Si la p(x ≤ NÚMERO) = 4% , calcule ese número.
Hola! No comprendo de dónde salió el -0.67 de 0.25 en la tabla. Si pueden aclarar mis dudas agradezco de antemano.
Feliz día!
En la primera tabla ubica el valor 0.2514 en la octava columna y a la izquierda tienes -0.6 y hacia arriba es 0.07 lo que implica -0.67
Hola,La probabilidad de que la rentabilidad sea mayor a 0,33 con un promedio de 0,23 aplicando la distribución normal, con los siguientes datos es:
escenario probabilidad rentabilidad
optimista 0,25 0,26
normal 0,65 0,30
pesimista 0,10 – 0,35
a.30,10 %
b.29,81 %
c.28,85 %
d.29,15 %