Capítulos
Resolver la ecuación de Schrödinger para el átomo de hidrógeno, se convierte en un problema tridimensional lo que hace que aparezca una nueva característica que no existía en las soluciones de la ecuación de Schrödinger en una dimensión. Esta característica es el momento angular del electrón y se debe al movimiento del electrón alrededor del núcleo, el cual se denomina momento angular orbital.
Cuando se resuelve la ecuación de Schrödinger en tres dimensiones, empleando coordenadas esféricas, para el átomo de hidrógeno, tres números cuánticos aparecen en la solución matemática.
Números cuánticos
Dependiendo de los valores de los números cuánticos, se obtienen diferentes soluciones para la ecuación de onda, las cuales permiten conocer las regiones de máxima probabilidad para ubicar un electrón en el interior de un átomo. A continuación tenemos los tres números cuánticos obtenidos de la función de onda:
Número cuántico principal
Representado por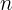 
y toma los valores enteros positivos 1, 2, 3, ...; su valor indica la órbita o nivel energético en el que se encuentra el electrón, mientras mayor sea el valor de 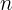, más alejado está el electrón del núcleo, y mayor es su contenido energético.
Número cuántico secundario
También conocido como el número cuántico del momento angular representado por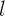 
. La solución matemática muestra que 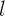toma los siguientes valores enteros
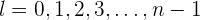
Cuando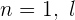 
toma el valor 
.
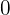Cuando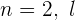 
toma los valores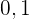 
Cuando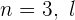 
toma los valores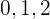 
El valor 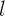indica la subórbita o subnivel de energía en el que se encuentra el electrón; esta subórbita o subnivel energético, también llamado orbital, se puede entender como la forma geométrica que describe el electrón al moverse dentro del átomo. Estas formas geométricas son diferentes para cada valor de 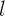, y a cada orbital se le asigna una literal
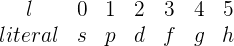
La magnitud del vector del momento angular es
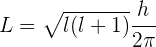
Número cuántico magnético
El tercer número cuántico que surge de la solución de la ecuación de Schrödinger se conoce como número cuántico magnético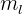 
, el cual puede adquirir valores de 
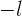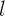a en los valores enteros.
Cuando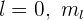 
toma el valor .
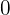Cuando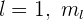 
toma los valores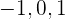 
Cuando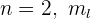 
toma los valores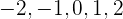 
El valor de 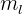indica las orientaciones que tienen los orbitales en el espacio y matemáticamente especifica la componente 
del vector de momento angular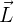 
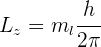
Si conocemos la magnitud de 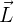, podemos determinar el ángulo 
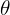entre 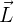y el eje
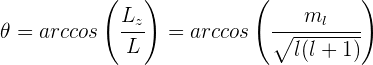
La fórmula anterior muestra que no se permite que existan todos los ángulos 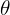, sino sólo los correspondientes a los valores de 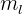. A esta restricción de las direcciones del vector del momento angular 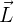se le conoce como cuantización espacial.
Número cuántico spin
El cuarto número cuántico se denota por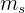 
y se le denomina número cuántico de espin o de giro del electrón. Este número tiene dos valores por cada valor del número cuántico 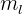; los valores son 
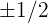y denotan los dos posibles giros del electrón alrededor de su propio eje.
Este número cuántico no proviene de la solución de la ecuación de Schrödinger, se obtiene con un cálculo más avanzado que combina la mecánica cuántica con la relatividad. La componente del momento angular del spin viene dado por
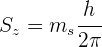
La magnitud del vector del momento angular del spin es
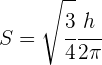
Niveles de energía
Consideramos un pozo infinito de ancho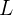 
y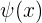 
la función de onda obtenida de la ecuación de Schödinger, que describe la onda de materia asociada a un electrón en un pozo infinito. Suponemos la energía potencial del electrón igual a cero, luego la totalidad de la energía del electrón atrapado es cinética. Así, la magnitud de los momentos lineales permitidos del electrón está dada por
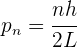
Si se conocen los momentos lineales cuánticos permitidos, los niveles de energía correspondientes están dados por
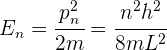
donde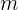 
es la masa del electrón, 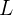el ancho del pozo, 
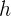la constante de Planck y 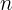el número cuántico principal.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Profesor Gaspar. Como puedo tener Coordenadas a traves del Espacio Exterior, para conocer por ejemplo la posible ubicacion de una tripulacion. Gracias Profesor.
Hola tu pregunta es muy interesante, para tener coordenadas en el espacio tendrías que tomar un cuerpo celeste, un sistema solar u otra cosa como referencia, podría ser también el sol o el planeta tierra y a partir de allí te podrías guiar, usando la forma rectangular, cilíndrica o esférica.
Un cordial saludo. Con respecto a la Constante de Planck, y asumiendo que puede ser un tema “interesante” a colegiar, quiero compartir la siguiente “observación”:
Si tenemos en cuenta que:
1ro- En los eventos de comportamiento Oscilatorio está conceptualizado claramente que la “frecuencia” es la cantidad de Oscilaciones que ejecuta la onda en un intervalo de tiempo determinado (por ejemplo, “20 Oscilaciones/segundo”) aunque por motivos prácticos en las ecuaciones aparezca anotada generalmente en la unidad “1/segundo”, lo cual tiene su origen en que el “periodo” se expresa también habitualmente en “segundos” (PERO, su unidad de medida conceptualmente rigurosa es “tiempo/Oscilación”)
2do- En base a lo anterior si ahora se procediera a anotar la “frecuencia” en su unidad “académicamente rigurosa” para enunciar la Ecuación Cuántica de la Energía de un fotón ( E = h x f ), entonces para que la unidad de medida de la Energía (E) quede en su unidad (por ejemplo, “Joules”) la unidad de medida de la Constante de Planck tendría que ser “(Joules x segundo)/OSCILACIÓN” (?!)
Un cordial saludo. Con respecto a las discusiones ontológicas sobre la Mecánica Cuántica, se puede «demostrar» que su causa básica radica en el hecho de que «la unidad de medida de la Constante de Planck adolece de un término, y que al ser agregado se nos revela de manera plena el verdadero significado físico de esta Constante, y a la vez se solucionan las aparentes Paradojas asociadas a la Mecánica Cuántica»!
Un cordial saludo. Con respecto a las «aparentes» Paradojas asociadas a la mecánica Cuántica, resulta que se puede «demostrar» que la causa básica de las mismas radica en que «la unidad de medida de la Constante de Planck adolece (le falta) de un término, que al ser adicionado permite comprender a plenitud el significado físico real de esta»!
Hola, agradecemos mucho tus comentarios para entender temas tan complicados de la mecánica cuántica y de las paradojas pues en si estas son difíciles de entender.
Un cordial saludo. Con respecto a la «unidad de medida» de la Constante de Planck, si tenemos en cuenta que para la «frecuencia» de los fenómenos oscilatorios, la cual tradicionalmente se expresa en la unidad «1/segundo» (por una cuestión de índole práctico a partir de que el período también se denota en la unidad «tiempo»), está bien determinado que la unidad de medida académicamente rigurosa para la «frecuencia» es el «Hz (OSCILACIONES/segundo)» y para el «período» es «tiempo/OSCILACIÓN», con estos antecedentes si ahora queremos expresar la ecuación cuántica de la energía de un fotón ( E = h x f ) usando esta unidad de medida de la «frecuencia» (para lo cual se tiene no solo el derecho sino que resulta ser el planteamiento MÁS CORRECTO ya que conceptualmente la frecuencia es «cantidad de OSCILACIONES/tiempo») entonces , expresando la Energía en «Joules» y el Tiempo en «segundos», y tener ahora que cancelar no solo la unidad «segundo» sino TAMBIÉN la unidad «OSCILACIÓN» entonces a la Constante de Planck le corresponde la unidad de medida «(Joules.segundo)/OSCILACIÓN»!
Hola tienes razón en cuanto a lo tradicional y lo riguroso, en este artículo nos basamos mas en lo tradicional pues solo es una iniciación en este tipos de temas de física, pero tu información es muy interesante y ayuda mucho para aquellos que desean profundizar en lo riguroso, te agradecemos mucho.
Buenas tardes.Por favor me puedes ayudar aplicando la integración o diferencial en la inecuacion de Heisenberg?.Soy cubana