Te presentamos una serie de ejercicios interactivos de la ecuación de Schrödinger en diversos contextos.Esperamos que estos ejercicios interactivos te brinden una comprensión más profunda y práctica de este fascinante principio cuántico.
La función de onda normalizada de una partícula que se encuentra encerrada en una caja de longitud 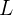 es...
es...
Selecciona una respuesta.
El nivel de energía de un electrón para el estado cuántico n es...
Selecciona una respuesta.
Un electrón se encuentra confinado en una caja de longitud 0.13 nm. La energía del electrón para el tercer estado cuántico es...
Selecciona una respuesta.
1 Identificamos los valores conocidos
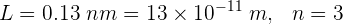
También se sabe que la masa de un electrón es 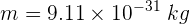 y la constante de Planck es
y la constante de Planck es 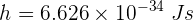
2 Calculamos el tercer nivel de energía
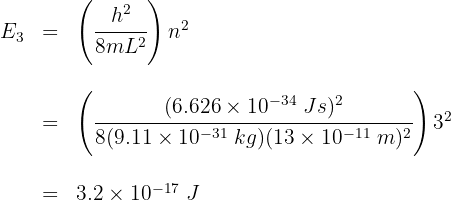
3 Convertimos a electronvoltios
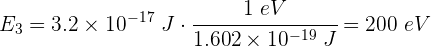
La frecuencia de luz emitida cuando un electrón que se encuentra confinado en una caja de longitud 0.4 nm, pasa del segundo nivel de energía al primero es...
Selecciona una respuesta.
1 Identificamos los valores conocidos
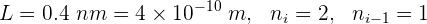
También se sabe que la masa de un electrón es 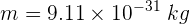 y la constante de Planck es
y la constante de Planck es 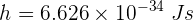
2 La energía de transición es
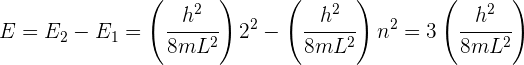
3 La frecuencia se obtiene de
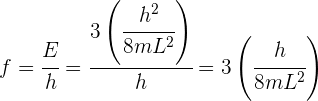
4 Calculamos la frecuencia
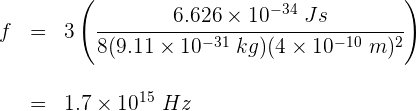
La longitud de onda de luz emitida cuando un electrón que se encuentra confinado en una caja de longitud 0.32 nm, pasa del segundo nivel de energía al primero es...
Selecciona una respuesta.
1 Identificamos los valores conocidos
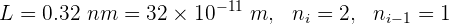
También se sabe que la masa de un electrón es 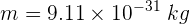 , la constante de Planck es
, la constante de Planck es 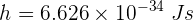 y la velocidad de la luz es
y la velocidad de la luz es 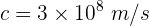
2 La longitud de onda viene dada por
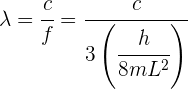
3 la longitud de onda
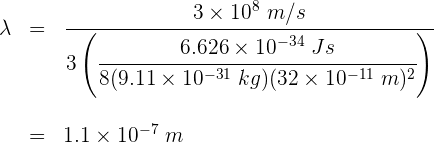
La rapidez mínima de un electrón que se encuentra confinado en una caja de longitud 0.27 nm es...
Selecciona una respuesta.
1 Identificamos los valores conocidos
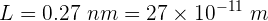
También se sabe que la masa de un electrón es 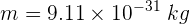 y la constante de Planck es
y la constante de Planck es 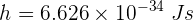
2 La rapidez mínima corresponde al estado 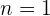 . Calculamos el primer nivel de energía
. Calculamos el primer nivel de energía
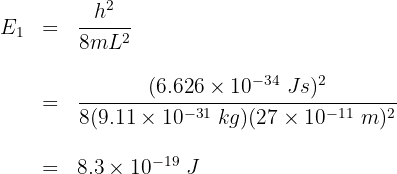
3 Como la energía total es igual a la cinética, ya que el electrón se encuentra en movimiento, tenemos
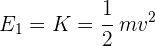
4 Sustituimos los datos conocidos y despejamos la velocidad
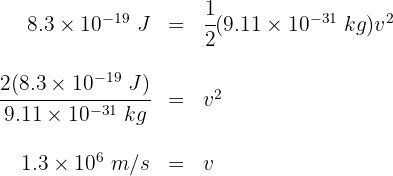
Un objeto de 3 mg se encuentra confinado en una caja de longitud 1.2 cm. La rapidez mínima del objeto es...
Selecciona una respuesta.
1 Identificamos los valores conocidos
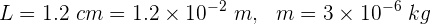
También se sabe que la constante de Planck es 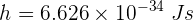
2 La rapidez mínima corresponde al estado 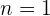 . Calculamos el primer nivel de energía
. Calculamos el primer nivel de energía
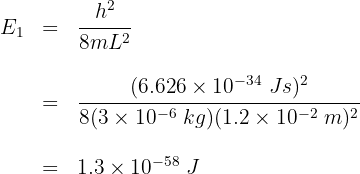
3 Como la energía total es igual a la cinética, ya que el electrón se encuentra en movimiento, tenemos
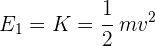
4 Sustituimos los datos conocidos y despejamos la velocidad
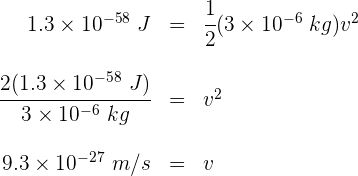
Una partícula se encuentra encerrada en una caja de longitud 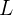 . La probabilidad de que la partícula se encuentre la región
. La probabilidad de que la partícula se encuentre la región 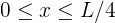 para
para 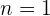 es...
es...
Selecciona una respuesta.
1 La función de onda normalizada es
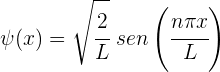
2 La probabilidad solicitada se obtiene de resolver
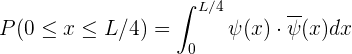
3 Resolviendo la integral para la función normalizada se obtiene
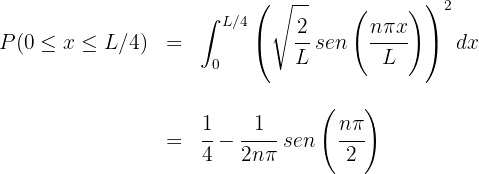
4 Cuando 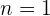 , se tiene que
, se tiene que 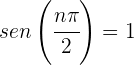 , luego
, luego
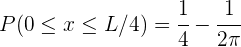
Una partícula se encuentra encerrada en una caja de longitud 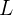 . La probabilidad de que la partícula se encuentre la región
. La probabilidad de que la partícula se encuentre la región 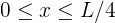 para
para 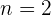 es...
es...
Selecciona una respuesta.
1 La función de onda normalizada es
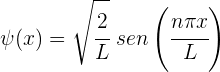
2 La probabilidad solicitada se obtiene de resolver
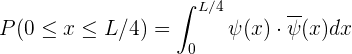
3 Resolviendo la integral para la función normalizada se obtiene
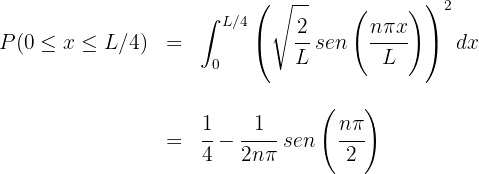
4 Cuando 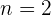 , se tiene que
, se tiene que 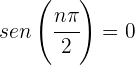 , luego
, luego
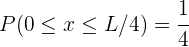
Una partícula se encuentra encerrada en una caja de longitud 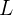 . La probabilidad de que la partícula se encuentre la región
. La probabilidad de que la partícula se encuentre la región 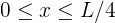 para
para 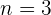 es...
es...
Selecciona una respuesta.
1 La función de onda normalizada es
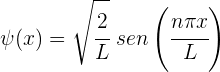
2 La probabilidad solicitada se obtiene de resolver
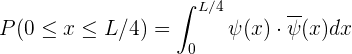
3 Resolviendo la integral para la función normalizada se obtiene
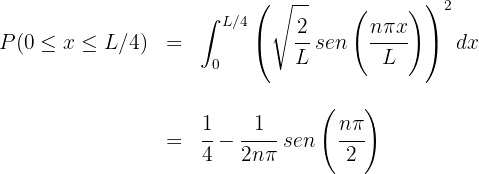
4 Cuando 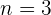 , se tiene que
, se tiene que 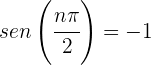 , luego
, luego
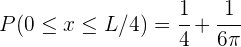
Si tienes dudas puedes consultar la teoría.
Resumir con IA:



Profesor Gaspar. Como puedo tener Coordenadas a traves del Espacio Exterior, para conocer por ejemplo la posible ubicacion de una tripulacion. Gracias Profesor.
Hola tu pregunta es muy interesante, para tener coordenadas en el espacio tendrías que tomar un cuerpo celeste, un sistema solar u otra cosa como referencia, podría ser también el sol o el planeta tierra y a partir de allí te podrías guiar, usando la forma rectangular, cilíndrica o esférica.
Un cordial saludo. Con respecto a la Constante de Planck, y asumiendo que puede ser un tema “interesante” a colegiar, quiero compartir la siguiente “observación”:
Si tenemos en cuenta que:
1ro- En los eventos de comportamiento Oscilatorio está conceptualizado claramente que la “frecuencia” es la cantidad de Oscilaciones que ejecuta la onda en un intervalo de tiempo determinado (por ejemplo, “20 Oscilaciones/segundo”) aunque por motivos prácticos en las ecuaciones aparezca anotada generalmente en la unidad “1/segundo”, lo cual tiene su origen en que el “periodo” se expresa también habitualmente en “segundos” (PERO, su unidad de medida conceptualmente rigurosa es “tiempo/Oscilación”)
2do- En base a lo anterior si ahora se procediera a anotar la “frecuencia” en su unidad “académicamente rigurosa” para enunciar la Ecuación Cuántica de la Energía de un fotón ( E = h x f ), entonces para que la unidad de medida de la Energía (E) quede en su unidad (por ejemplo, “Joules”) la unidad de medida de la Constante de Planck tendría que ser “(Joules x segundo)/OSCILACIÓN” (?!)
Un cordial saludo. Con respecto a las discusiones ontológicas sobre la Mecánica Cuántica, se puede «demostrar» que su causa básica radica en el hecho de que «la unidad de medida de la Constante de Planck adolece de un término, y que al ser agregado se nos revela de manera plena el verdadero significado físico de esta Constante, y a la vez se solucionan las aparentes Paradojas asociadas a la Mecánica Cuántica»!
Un cordial saludo. Con respecto a las «aparentes» Paradojas asociadas a la mecánica Cuántica, resulta que se puede «demostrar» que la causa básica de las mismas radica en que «la unidad de medida de la Constante de Planck adolece (le falta) de un término, que al ser adicionado permite comprender a plenitud el significado físico real de esta»!
Hola, agradecemos mucho tus comentarios para entender temas tan complicados de la mecánica cuántica y de las paradojas pues en si estas son difíciles de entender.
Un cordial saludo. Con respecto a la «unidad de medida» de la Constante de Planck, si tenemos en cuenta que para la «frecuencia» de los fenómenos oscilatorios, la cual tradicionalmente se expresa en la unidad «1/segundo» (por una cuestión de índole práctico a partir de que el período también se denota en la unidad «tiempo»), está bien determinado que la unidad de medida académicamente rigurosa para la «frecuencia» es el «Hz (OSCILACIONES/segundo)» y para el «período» es «tiempo/OSCILACIÓN», con estos antecedentes si ahora queremos expresar la ecuación cuántica de la energía de un fotón ( E = h x f ) usando esta unidad de medida de la «frecuencia» (para lo cual se tiene no solo el derecho sino que resulta ser el planteamiento MÁS CORRECTO ya que conceptualmente la frecuencia es «cantidad de OSCILACIONES/tiempo») entonces , expresando la Energía en «Joules» y el Tiempo en «segundos», y tener ahora que cancelar no solo la unidad «segundo» sino TAMBIÉN la unidad «OSCILACIÓN» entonces a la Constante de Planck le corresponde la unidad de medida «(Joules.segundo)/OSCILACIÓN»!
Hola tienes razón en cuanto a lo tradicional y lo riguroso, en este artículo nos basamos mas en lo tradicional pues solo es una iniciación en este tipos de temas de física, pero tu información es muy interesante y ayuda mucho para aquellos que desean profundizar en lo riguroso, te agradecemos mucho.
Buenas tardes.Por favor me puedes ayudar aplicando la integración o diferencial en la inecuacion de Heisenberg?.Soy cubana