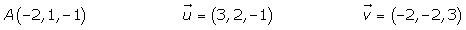Ecuación vectorial del plano
Para determinar un plano del espacio se necesita conocer un punto P y un par de vectores que formen una base, es decir, que sean linealmente independientes.

Para que el punto P pertenezca al plano π el vector 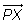
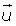
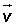
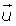
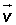
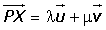
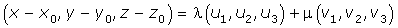
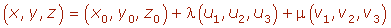
Ecuaciones paramétricas del plano
Si operamos en la ecuación vectorial del plano llegamos a la igualdad:
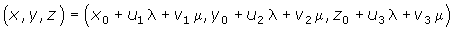
Para que se verifique esta igualdad, se debe cumplir que:
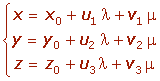
Ecuación general o implícita del plano
Un punto está en el plano π si tiene solución el sistema:

Este sistema tiene que ser compatible determinado en las incógnitas λ y µ· Por tanto el determinante de la matriz ampliada del sistema con la columna de los términos independientes tiene que ser igual a cero.

Desarrollando el determinante obtenemos:

Damos los valores:

Sustituimos:
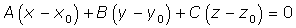
Realizamos las operaciones y le damos a D el valor:
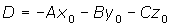
Obtenemos la ecuación general de plano:

Ecuación canónica o segmentaria del plano
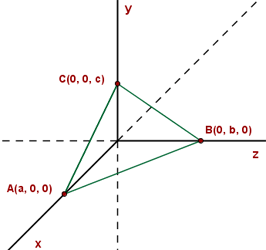
Sean los puntos A(a, 0, 0), B(0, b, 0) y C(0, 0, c), la ecuación canónica viene dada por:
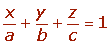

Ejercicios
1.
Hallar las ecuaciones paramétricas e implícitas del plano que pasa por el punto A(1, 1, 1) y tiene como vectores directores a
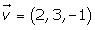



2.
Hallar las ecuaciones paramétricas e implícitas del plano que pasa por los puntos A(−1, 2, 3) y B(3, 1, 4) y contiene al vector
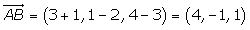
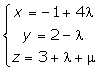
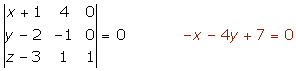
3.
Hallar las ecuaciones paramétricas e implícitas del plano que pasa por los puntos A(−1, 1, −1), B(0, 1, 1) y C(4, −3, 2).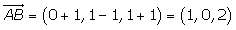


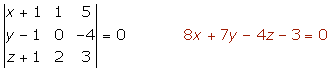
4.
Sea π el plano de ecuaciones paramétricas: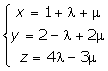
Se pide comprobar si los puntos A (2, 1, 9/2) y B(0, 9, −1) pertenecen al plano.


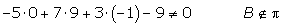
5.
Hallar la ecuación segmentaria del plano que pasa por los puntos A(1, 1, 0), B(1, 0, 1) y C(0, 1, 1).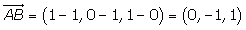
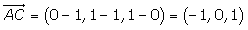

Dividiendo por −2 obtenemos la ecuación segmentaria:
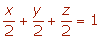
6.
Hallar la ecuación del plano que pasa por el punto A(2, 0, 1 y contiene a la recta de ecuación:
De la ecuación de la recta obtenemos el punto B y el vector 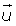

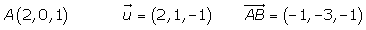

7.
Hallar la ecuación del plano que pasa por los puntos A(1, −2, 4), B(0, 3, 2) y es paralelo a la recta: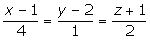
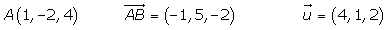
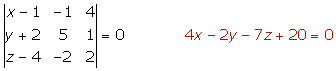
8.
Dadas las rectas
Determinar la ecuación del plano que contiene a r y es paralelo a s.