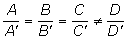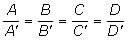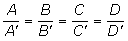Para estudiar la posición relativa de tres planos discutimos el sistema:

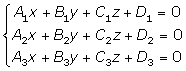
Explicaciones y ejemplos de posiciones relativas de tres planos - 1

Y sean:

r = rango de la matriz de los coeficientes.

r'= rango de la matriz ampliada.

Las posicones relativas de los tres planos vienen dada por la siguiente tabla:

r r' Posición
3 3 1. Planos secantes en un punto
2 3
Explicaciones y ejemplos de posiciones relativas de tres planos - 2
2.1 Planos secantes dos a dos.
2.2 Dos planos paralelos y el tercero secante.
2 2
Explicaciones y ejemplos de posiciones relativas de tres planos - 3
3.1 Planos secantes y distintos.
3.2 Dos planos coincidentes y uno secante.
1 2
Explicaciones y ejemplos de posiciones relativas de tres planos - 4
4.1 Planos paralelos y distintos dos a dos.
4.2 Planos paralelos y dos coincidentes.
1 1 5. Planos coincidentes.

1. Planos secantes en un punto

r=3, r'=3

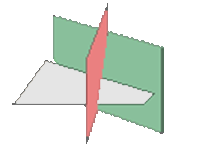
Explicaciones y ejemplos de posiciones relativas de tres planos - 5

2.1 Planos secantes dos a dos.

r = 2, r' = 3

Los tres planos forman una superficie prismática.

Explicaciones y ejemplos de posiciones relativas de tres planos - 6

2.1 Dos planos paralelos y el tercero secante

r = 2, r' = 3

Dos filas de la matriz de los coeficientes son proporcionales.

Explicaciones y ejemplos de posiciones relativas de tres planos - 7

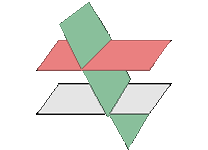
Explicaciones y ejemplos de posiciones relativas de tres planos - 8

3.1 Planos secantes y distintos

r = 2, r' = 2

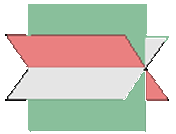
Explicaciones y ejemplos de posiciones relativas de tres planos - 9

3.2 Dos planos coincidentes y uno secante

r = 2, r' = 2

Dos filas de la matriz ampliada son proporcionales.

Explicaciones y ejemplos de posiciones relativas de tres planos - 10

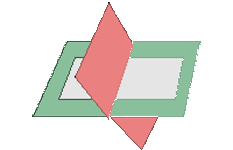
Explicaciones y ejemplos de posiciones relativas de tres planos - 11

4.1 Planos paralelos y distintos dos a dos

r = 1, r' = 2

Explicaciones y ejemplos de posiciones relativas de tres planos - 12

4.2 Planos paralelos y dos coincidentes

r = 1, r' = 2

Dos filas de la matriz ampliada son proporcionales.

Explicaciones y ejemplos de posiciones relativas de tres planos - 13

Explicaciones y ejemplos de posiciones relativas de tres planos - 14

5. Planos coincidentes

r = 1, r' = 1

Explicaciones y ejemplos de posiciones relativas de tres planos - 15

Ejemplos

Hallar la posición relativa de los planos:

1. Explicaciones y ejemplos de posiciones relativas de tres planos - 16

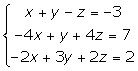
Explicaciones y ejemplos de posiciones relativas de tres planos - 17

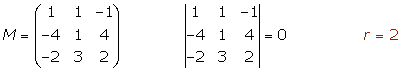
Explicaciones y ejemplos de posiciones relativas de tres planos - 18

Explicaciones y ejemplos de posiciones relativas de tres planos - 19

Los tres planos son secantes dos a dos y forman una superficie prismática.

2. Explicaciones y ejemplos de posiciones relativas de tres planos - 20

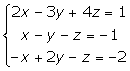
Explicaciones y ejemplos de posiciones relativas de tres planos - 21

Explicaciones y ejemplos de posiciones relativas de tres planos - 22

Explicaciones y ejemplos de posiciones relativas de tres planos - 23

Los tres planos se cortan en un punto.

3. Explicaciones y ejemplos de posiciones relativas de tres planos - 24

Explicaciones y ejemplos de posiciones relativas de tres planos - 25

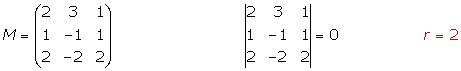
Explicaciones y ejemplos de posiciones relativas de tres planos - 26

Explicaciones y ejemplos de posiciones relativas de tres planos - 27

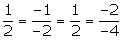
Explicaciones y ejemplos de posiciones relativas de tres planos - 28

El segundo y tercer plano son coincidentes y el primero es secante a ellos, por tanto los tres planos se cortan en una recta.

4. Explicaciones y ejemplos de posiciones relativas de tres planos - 29

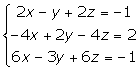
Explicaciones y ejemplos de posiciones relativas de tres planos - 30

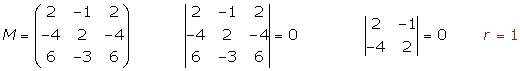
Explicaciones y ejemplos de posiciones relativas de tres planos - 31

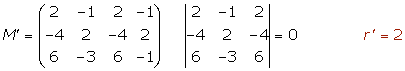
Explicaciones y ejemplos de posiciones relativas de tres planos - 32

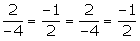
Explicaciones y ejemplos de posiciones relativas de tres planos - 33

El primer y segundo plano son coincidentes y el tercero es paralelo a ellos.