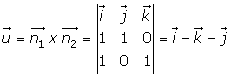Ecuación vectorial de la recta
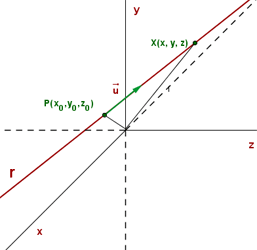
Definimos una recta r como el conjunto de los puntos del plano, alineados con un punto P y con una dirección dada 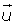
Si P(x1, y1) es un punto de la recta r, el vector 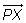

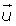

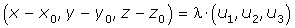

Ecuaciones paramétricas de la recta
Si operamos en la ecuación vectorial de la recta llegamos a la igualdad:
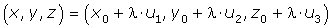
Para que se verifique esta igualdad, se deben cumplir:

Ecuaciones continuas de la recta
Despejando e igualando λ en las ecuaciones paramétricas se tiene:
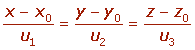
Ecuaciones implícitas de la recta
Una recta puede venir determinada por la intersección de los planos.
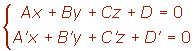
Si en las ecuaciones continuas de la recta quitamos denominadores y pasamos todo al primer miembro, obtenemos también las ecuaciones implícitas.
Ejercicios
1.
Hallar las ecuaciones paramétricas, en forma continua e implícitas de la recta que pasa por el punto A = (1, 2, 1) y cuyo vector director es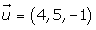
Ecuaciones paramétricas

Ecuaciones en forma continua
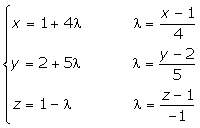
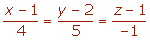
Ecuaciones implícitas

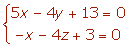
2.
Hallar las ecuaciones paramétricas, en forma continua e implícita de la recta que pasa por los puntos A(1, 0, 1) y B(0, 1, 1).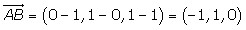

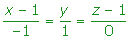
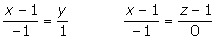

3.
Dada la recta r: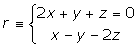
Hallar las ecuaciones en forma continua y paramétrica.
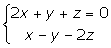
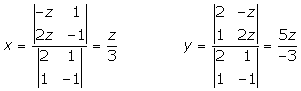


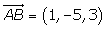
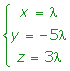
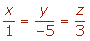
4.
Sea r la recta de ecuación: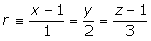
¿Pertenecen a r los puntos A(0, −2, −2) y B(3, 2, 6)?

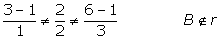
5.
Obtener la ecuación de la recta que, siendo paralela la recta dada por x = 3λ, y = λ, z = 2λ + 2, contiene al punto P(0, 1, −1).
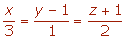
6.
Una recta es paralela a los planos x + y = 0, x + z = 0 y pasa por por el punto (2, 0, 0). Hallar sus ecuaciones.El vector director de la recta es perpendicular a a los vectores normales de cada plano.