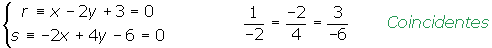Posiciones relativas de dos rectas en el plano
Ecuación explícita r ≡ y = mx +n s ≡ y = m'x +n' | Ecuación general r ≡ Ax +By +C =0 r ≡ Ax +By +C =0 | |
| r y s secantes | m ≠ m' | 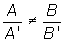 |
| r y s paralelas | m = m'n ≠ n' | 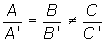 |
| r y s coincidentes | m = m'n = n' | 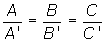 |
Secantes

Dos rectas son secantes si sólo tienen un punto en común.
El sistema de ecuaciones formado por las dos rectas tiene una solución.
Paralelas

Dos rectas son paralelas si no tienen ningún punto en común.
El sistema de ecuaciones formado por las dos rectas no tiene solución.
Coincidentes

Dos rectas son coincidentes si tienen todos los puntos son comunes.
El sistema de ecuaciones formado por las dos rectas tiene infinitas soluciones.
Ejemplo