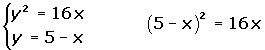Para hallar los puntos comunes a una cónica y una recta resolveremos el sistema formado por las ecuaciones de ambas.

En general se obtiene un ecuación de segundo grado, que tendrá dependiendo del signo del discrimínante, Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 1, las siguientes soluciones:

Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 2


1

Si Δ > 0

Dos soluciones: la recta y la cónica son secantes.

Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 3


2

Si Δ = 0

Una solución: la recta y la cónica son tangentes.

Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 4


3

Si Δ < 0

Ninguna solución: la recta y la cónica son exteriores.

Calcula la posición relativa de la circunferencia Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 5 y la recta Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 6.




Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 7

Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 8

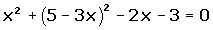
Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 9

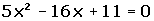
Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 10

Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 11

Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 12

Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 13

Estudiar la posición relativa de la circunferencia x2 + y2 - 4x + 2y - 20 = 0 con las rectas:

1

x + 7y -20 = 0

Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 14

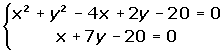
Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 15

Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 16

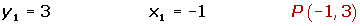
Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 17

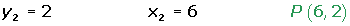
Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 18

Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 19

2

3x + 4y - 27 = 0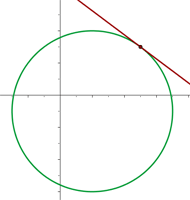

Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 20

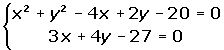
Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 21

Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 22

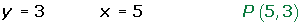
Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 23

Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 24

3

x + y - 10 = 0

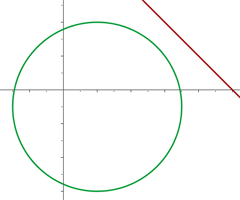
Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 25

Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 26

Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 27

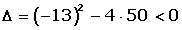
Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 28

Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 29


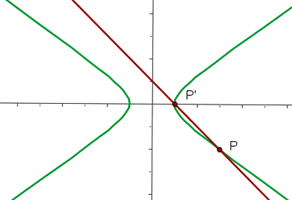
Determina la posición relativa de la recta x + y - 1 =0 con respecto a la hipérbola x2 - 2y2 = 1.

Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 30


Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 31

Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 32

Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 33


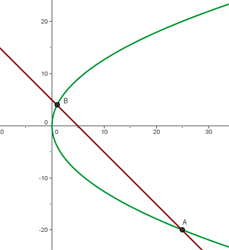
Calcular la posición relativa de la recta r ≡ x + y - 5 = 0 respecto a la parábola y2 = 16 x.

Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 34

Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 35

Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 36

Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 37

Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 38

Explicaciones y ejemplos de posiciones relativas de una cónica y una recta - 39