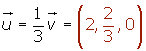Qué significa vectores en el espacio tridimensional en Matemáticas

Un vector en el espacio es cualquier segmento orientado que tiene su origen en un punto y su extremo en el otro.

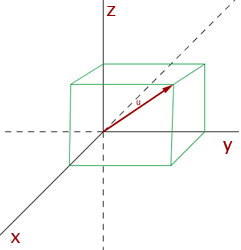
Componentes de un vector en el espacio

Si las coordenadas de A y B son: A(x₁, y₁, z₁) y B(x₂, y₂, z₂) Las coordenadas o componentes del vector son las coordenadas del extremo menos las coordenadas del origen.

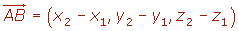
Determinar la componentes de los vectores que se pueden trazar el el triángulo de vértices A(−3, 4, 0), B(3, 6, 3) y C(−1, 2, 1).

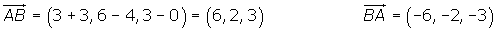
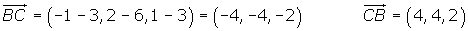
Módulo de un vector

El módulo de un vector es la longitud del segmento orientado que lo define.

El módulo de un vector es un número siempre positivo y solamente el vector nulo tiene módulo cero.

Cálculo del módulo conociendo sus componentes

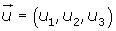
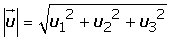
Dados los vectores y , hallar los módulos de y ·

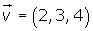
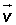
Cálculo del módulo conociendo las coordenadas de los puntos

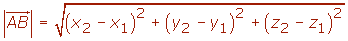
Distancia entre dos puntos

La distancia entre dos puntos es igual al módulo del vector que tiene de extremos dichos puntos.

Hallar la distancia entre los puntos A(1, 2, 3) y B(−1, 2, 0).

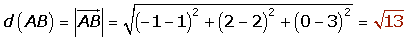
Vector unitario

Un vector unitario tiene de módulo la unidad.

La normalización de un vector consiste en asociarle otro vector unitario, de la misma dirección y sentido que el vector dado, dividiendo cada componente del vector por su módulo.

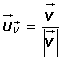
Operaciones de vectores en el espacio

Suma de vectores

Para sumar dos vectores se suman sus respectivas componentes.

Ejemplos

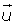
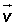
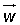
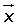
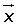
Dados = (2, 1, 3), = (1, −1, 0), = (1, 2, 3), hallar el vector = 2u + 3v − w.

= (4, 2, 6) + (3, −3, 0) − (1, 2, 3) = (6, −3, 3)

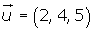
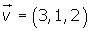
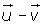
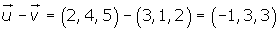
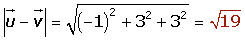
Dados los vectores y , hallar el módulo del vector .

Propiedades de la suma de vectores

Asociativa

+ ( + ) = ( + ) +

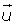
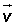
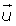
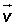
Conmutativa

+ = +

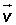
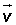
Elemento neutro

+ =

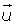
Elemento opuesto

+ (− ) =

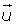
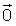
Producto de un número real por un vector

El producto de un número real k por un vector es otro vector:

De igual dirección que el vector .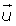

Del mismo sentido que el vector 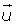si k es positivo.

De sentido contrario del vector si k es negativo.

De módulo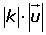

Las componentes del vector resultante se obtienen multiplicando por K las componentes del vector.

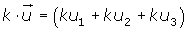
Propiedades del producto de un número por un vector

Asociativa

k · (k' · 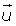) = (k · k') ·

Distributiva respecto a la suma de vectores

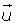
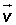
k · ( + ) = k · + k ·

Distributiva respecto a los escalares

(k + k') · = k · + k' ·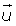

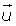
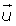
Elemento neutro

1 · =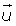

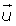
Ejemplo

Dado = (6, 2, 0) determinar de modo que sea 3 = .