Un vector fijo 
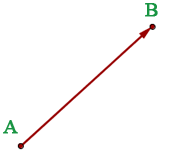
Un vector tiene:
Una dirección
La direcccíon del vector es la dirección de la recta que contiene al vector o de cualquier recta paralela a ella.
Un sentido
El sentido del vector 
Un módulo
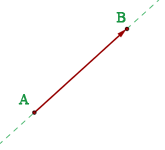
El módulo del vector 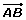

El módulo de un vector es un número siempre positivo o cero.
Módulo de un vector a partir de sus componentes
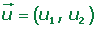

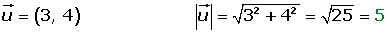
Módulo a partir de las coordenadas de los puntos


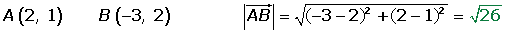
Coordenadas de un vector
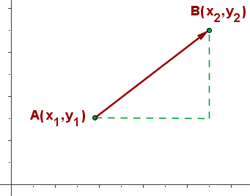
Si las coordenadas de los puntos extremos, A y B, son:
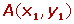
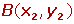
Las coordenadas del vector 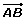
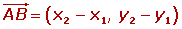
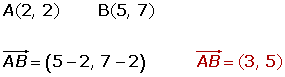
Clasificación de vectores
Vectores equipolentes

Dos vectores son equipolentes cuando tienen igual módulo, dirección y sentido.
Vectores libres

El conjunto de todos los vectores equipolentes entre sí se llama vector libre. Es decir los vectores libres tienen el mismo módulo, dirección y sentido.
Vectores fijos
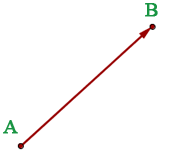
Un vector fijo es un representante del vector libre. Es decir, los vectores fijos tienen el mismo módulo, dirección, sentido y origen.
Vectores ligados

Los vectores ligados son vectores equipolentes que actúan en la misma recta. Es decir, los vectores fijos tienen el mismo módulo, dirección, sentido y se encuentran en la misma recta.
Vectores opestos

Los vectores opuestos tienen el mismo módulo, dirección, y distinto sentido.
Vectores unitarios
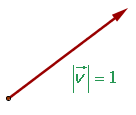
Los vectores untario tienen de módulo, la unidad.
Para obtener un vector unitario, de la misma dirección y sentido que el vector dado se divide éste por su módulo.
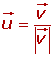
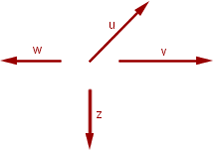
Vectores concurrentes

Los vectores concurrentes tienen el mismo origen.
Vector de posición

El vector 
Vectores linealmente dependientes

Varios vectores libres del plano son linealmente dependientes si existe una combinación lineal de ellos que sea igual al vector cero, sin que sean cero todos los coeficientes de la combinación lineal.

Vectores linealmente independientes
Varios vectores libres son linealmente independientes si ninguno de ellos se puede expresar como combinación lineal de los otros.
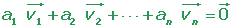
a1 = a2 = ··· = an = 0
Vectores ortogonales
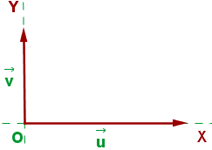
Dos vectores son ortogonales o perpendiculares si su producto escalar es cero.

Vectores ortonormales

Dos vectores son ortonormales si:

