Capítulos
- Sólo el dividendo es decimal
- Sólo el divisor es decimal
- El dividendo y el divisor son decimales
- División por la unidad seguida de ceros
- Raíz cuadrada de números decimales
- Pasar de decimal exacto a fracción
- Pasar de periódico puro a fracción generatriz
- Pasar de periódico mixto a fracción generatriz
- Redondeo
Sólo el dividendo es decimal
Se efectúa la división de números decimales como si de números enteros se tratara. Cuando bajemos la primera cifra decimal, colocamos una coma en el cociente y continuamos dividiendo.
Ejemplo
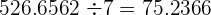
Sólo el divisor es decimal
Quitamos la coma del divisor y añadimos al dividendo tantos ceros como cifras decimales tenga el divisor. A continuación dividimos como si fueran números enteros.
Ejemplo
El dividendo y el divisor son decimales
Se iguala el número de cifras decimales del dividendo y del divisor, añadiendo a aquel que tenga menos decimales, tantos ceros como cifras decimales de diferencia haya. A continuación se prescinde de la coma, y dividimos como si fueran números enteros.
Ejemplo
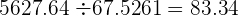
División por la unidad seguida de ceros
Para dividir un número por la unidad seguida de ceros, se desplaza la coma hacia la izquierda tantos lugares como ceros acompañen a la unidad.
Ejemplo
 |
 |
 |
 |
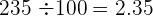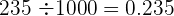Raíz cuadrada de números decimales
Para extraer la raíz cuadrada de un número decimal, debemos seguir los siguientes pasos:
1 Se separan grupos de dos cifras a partir de la coma hacia la izquierda (la parte entera) y hacia la derecha (la parte decimal).
2 Si el radicando tiene en su parte decimal un número impar de cifras, se añade un cero a la derecha.
3 Prescindiendo de la coma, se extrae la raíz cuadrada del número que resulta.
4 En la raíz, a partir de la derecha, colocamos un número de cifras decimales igual al número de pares de cifras decimales que hubiere en el radicando. En el resto y también a partir de la derecha, se separan tantas cifras decimales como haya en el radicando.
Ejemplo
Pasar de decimal exacto a fracción
Si la fracción es decimal exacta, la fracción tiene como numerador el número dado sin la coma, y por denominador, la unidad seguida de tantos ceros como cifras decimales tenga.
Ejemplo
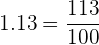
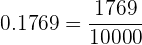
Pasar de periódico puro a fracción generatriz
Si la fracción es periódica pura, la fracción generatriz tiene como numerador el número dado sin la coma, menos la parte entera, y por denominador un número formado por tantos nueves como cifras tiene el período.
Ejemplo
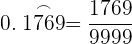
Pasar de periódico mixto a fracción generatriz
Si la fracción es periódica mixta, la fracción generatriz tiene como numerador el número dado sin la coma, menos la parte entera seguida de las cifras decimales no periódicas, y por denominador, un numero formado por tantos nueves como cifras tenga el período, seguidos de tantos ceros como cifras tenga la parte decimal no periódica.
Ejemplo
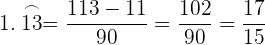
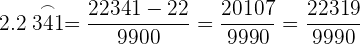
Redondeo
Para redondear números decimales tenemos que fijarnos en la unidad decimal posterior a la que queremos redondear. Si la unidad decimal es mayor o igual que 
, aumentamos en una unidad la unidad decimal anterior; en caso contrario, la dejamos como está.
Ejemplo
1 
como 
es menor que , entonces el número redondeado es 
.
2 
como 
es mayor que como es, entonces el número redondeado es 
.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
La suma de decimales del ejercicio 13 dan 107.82 y el resultado final es de 92.18.
Favor corregir
Hola, disculpa pero revise el ejercicio varias veces y el resultado me da 107.82, no se si podrías mencionar por que te da ese resultado.
La 5, 7 y 14 están incorrectas
Hola te agradecemos tus observaciones, pero podrías ser mas especifico en los errores pues no encontré lo que mencionas y para evitar las equivocaciones nos ayudaría mucho tus comentarios.
la 13 esta mal por los numeros. porfa corregir
Hola, una disculpa y agradecemos tu ayuda ya se corrigió.
pero finalmente el ultimo punto da 75???
Hola, podrias mencionar a qué ejercicio te refieres para contestar tu pregunta.