Capítulos
Decimal exacto
La parte decimal de un número decimal exacto está compuesta por una cantidad finita de términos.
Ejemplos:
- 15.125
- 0.1
- 3.0000001
Periódico puro
La parte decimal, llamada periodo, se repite infinitamente.
Ejemplos:
Periódico mixto
Su parte decimal está compuesta por una parte no periódica y una parte periódica o período.
Ejemplos:
No exactos y no periódicos
Hay números decimales que no pertenecen a ninguno de los tipos anteriores.
Ejemplo:
Clasificación de números decimales a partir de la fracción
Dada una fracción podemos determinar qué tipo de número decimal será.
Para esto tomamos el denominador y lo descomponemos en factores.
1 Si en sus factores sólo aparecen 2, 5 o ambos, la fracción es decimal exacta.
Ejemplos:
2 Si no aparece ningún 2 ó ningún 5, la fracción es periódica pura.
Ejemplos:
3 Si aparecen otros factores además del 2 ó el 5, la fracción es periódica mixta.
Ejemplos:
Resumir con IA:
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
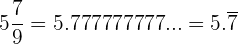
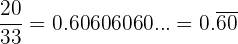
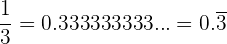
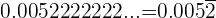
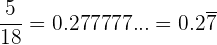
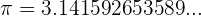
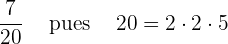
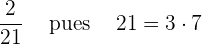
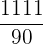
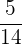
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
La suma de decimales del ejercicio 13 dan 107.82 y el resultado final es de 92.18.
Favor corregir
Hola, disculpa pero revise el ejercicio varias veces y el resultado me da 107.82, no se si podrías mencionar por que te da ese resultado.
La 5, 7 y 14 están incorrectas
Hola te agradecemos tus observaciones, pero podrías ser mas especifico en los errores pues no encontré lo que mencionas y para evitar las equivocaciones nos ayudaría mucho tus comentarios.
la 13 esta mal por los numeros. porfa corregir
Hola, una disculpa y agradecemos tu ayuda ya se corrigió.
pero finalmente el ultimo punto da 75???
Hola, podrias mencionar a qué ejercicio te refieres para contestar tu pregunta.