Calcula las siguientes multiplicaciones:
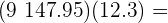
Este campo es obligatorio.
Recuerda que para resolver multiplicaciones con punto decimal realizamos la operación multiplicación y al final colocamos el punto decimal en la suma de posiciones a la derecha del punto de los números a multiplicar, es decir,

Se coloca el punto decimal en la tercera posición, que es la suma de posiciones a la derecha de los números originales.
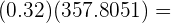
Este campo es obligatorio.
Recuerda que para resolver multiplicaciones con punto decimal realizamos la operación multiplicación y al final colocamos el punto decimal en la suma de posiciones a la derecha del punto de los números a multiplicar, es decir,

Se coloca el punto decimal en la 6ta posición, que es la suma de posiciones a la derecha de los números originales.
Resuelve las siguientes multiplicaciones por la unidad seguida de cero:
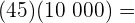
Este campo es obligatorio.
Esta multiplicación es diferente, ya que basta con multiplicar el 45 por 1 y agregar el mismo número de ceros.
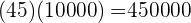
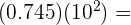
Este campo es obligatorio.
Comenzamos por resolver la potencia y luego multiplicamos el 0.745 por 1 y mover el punto decimal el mismo número de ceros, es decir, 2 posiciones a la derecha.
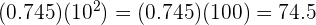
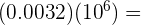
Este campo es obligatorio.
Comenzamos por resolver la potencia y luego multiplicamos el 0.0032 por 1 y mover el punto decimal el mismo número de ceros, es decir, 6 posiciones a la derecha.
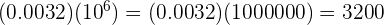

Este campo es obligatorio.
Comenzamos por resolver la potencia y luego multiplicamos el 84.58 por 1 y mover el punto decimal el mismo número de ceros, es decir, 2 posiciones a la derecha.

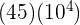 =
=
Este campo es obligatorio.
Comenzamos por resolver la potencia y luego multiplicamos el 45 por 1 y agregamos el mismo número de ceros.


Este campo es obligatorio.
Multiplicamos el 9.15 por 1 y agregamos el mismo número de ceros.

 =
=
Este campo es obligatorio.
Comenzamos por resolver la potencia y luego multiplicamos el 0.27 por 1 y agregamos el mismo número de ceros, es decir, 3 posiciones a la derecha.


Este campo es obligatorio.
Comenzamos por multiplicar 15.169 por 1 y agregamos el mismo número de ceros, es decir, 2 posiciones a la derecha.

Resuelve los siguientes problemas:
En una empresa de zumos se fabrica un producto que es mezcla de los jugos de tres frutas distintas, entre ellas el jugo de piña. Ayer se embotellaron 20 botellas de 1.5 litros cada una. Si cada litro de zumo contiene 0.25 litros de jugo de piña, ¿cuánto jugo de esta fruta se consumió ayer?
 .
.
Este campo es obligatorio.
Ayer se consumieron 7.5 l. de jugo de piña.
Comenzamos por calcular la cantidad de jugo de piña por botella

Se gastan 0.375 litros de jugo de piña en cada botella.
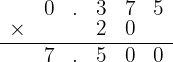
Se gastan 7.5 litros de jugo de piña en total.
En la etiqueta que marca la información nutricional de cierta marca de yogures se indica que cada 100g de producto contiene 2.6 g de grasas. ¿Sabrías decir cuánta grasa tomaríamos si nos comemos 200 g de yogur?
 .
.
Este campo es obligatorio.
Tomaríamos 5.2 g. de grasas.
Si por 100g de producto se tiene 2.6g de grasa entonces para saber cuánta grasa se tiene en 200g de yogur, bastaría con multiplicar por 2 el número de grasa, es decir,
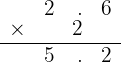
Si tienes dudas puedes consultar la teoría
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
La suma de decimales del ejercicio 13 dan 107.82 y el resultado final es de 92.18.
Favor corregir
Hola, disculpa pero revise el ejercicio varias veces y el resultado me da 107.82, no se si podrías mencionar por que te da ese resultado.
La 5, 7 y 14 están incorrectas
Hola te agradecemos tus observaciones, pero podrías ser mas especifico en los errores pues no encontré lo que mencionas y para evitar las equivocaciones nos ayudaría mucho tus comentarios.
la 13 esta mal por los numeros. porfa corregir
Hola, una disculpa y agradecemos tu ayuda ya se corrigió.
pero finalmente el ultimo punto da 75???
Hola, podrias mencionar a qué ejercicio te refieres para contestar tu pregunta.