Ejercicios propuestos
Ordena de menor a mayor estos números decimales:
a
b
a El orden quedaría de la siguiente manera 
b El orden del segundo conjunto de números quedaría

Ordena de mayor a menor estos números decimales:
a
b
a El orden quedaría de la siguiente manera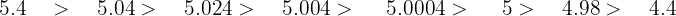
b El orden del segundo conjunto de números quedaría

Clasificar, por el tipo, los números decimales correspondientes a las fracciones:

En esta clasificación empleamos divisiones
a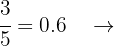 Decimal exacto
Decimal exacto
b Periódico mixto
Periódico mixto
c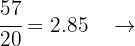 Decimal exacto
Decimal exacto
d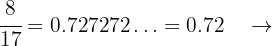 Periódico puro
Periódico puro
e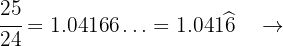 Periódico mixto
Periódico mixto
f Periódico puro
Periódico puro
Clasificar, por el tipo, los números decimales correspondientes a las fracciones:
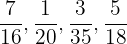
En esta clasificación, descomponemos el denominador en factores:
a Decimal exacto
Decimal exacto
b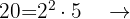 Decimal exacto
Decimal exacto
c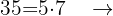 Periódico mixto
Periódico mixto
d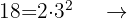 Periódico mixto
Periódico mixto
Realizar las siguientes multiplicaciones con números decimales:
a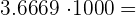
b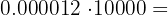
c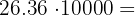
d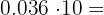
e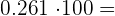
Para multiplicar un número por la unidad seguida de ceros, se desplaza la coma hacia la derecha tantos lugares como ceros acompañen a la unidad
a 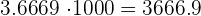
b 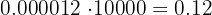
c 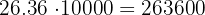
d 
e 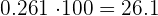
Realizar las siguientes operaciones con números decimales:
a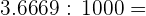
b
c
d
e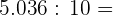
Para dividir un número por la unidad seguida de ceros, se desplaza la coma hacia la izquierda tantos lugares como ceros acompañen a la unidad
a 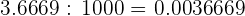
b 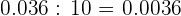
c 
d 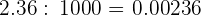
e 
Indica la parte entera y decimal de los siguientes números decimales:
a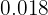
b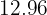
c
a 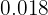 tiene parte entera 0 y su parte decimal es 018
tiene parte entera 0 y su parte decimal es 018
b 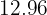 tiene parte entera 12 y su parte decimal es 96
tiene parte entera 12 y su parte decimal es 96
c  tiene parte entera 32 y su parte decimal es 473
tiene parte entera 32 y su parte decimal es 473
Redondea hasta las décimas y centécimas los siguientes números decimales
a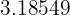
b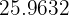
c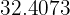
a 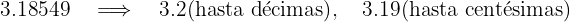
b 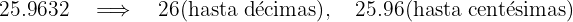
c 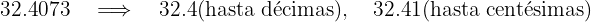
Truncar hasta las décimas y centécimas los siguientes números decimales
a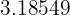
b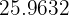
c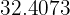
a 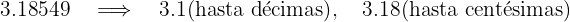
b 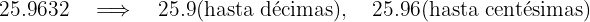
c 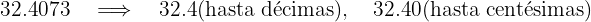
Resuelve las siguientes divisiones de números decimales:
a
b
a  Para resolver la siguiente división, multiplicamos arriba y abajo por
Para resolver la siguiente división, multiplicamos arriba y abajo por  :
:
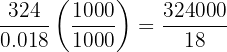
esto no afecta el resultado, pues obtenemos una fracción equivalente. Ahora, procedemos a realizar la división de manera usual con números enteros
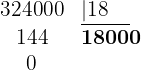
b 
En este caso, realizamos la operación de manera usual, como si estuviéramos trabajando con enteros pero con la única diferencia que cuando bajemos el numero después del punto, colocamos un punto decimal en el cociente

aqui, primero vimos que el  cabía dos veces en el
cabía dos veces en el  , despues colocamos el punto despues del
, despues colocamos el punto despues del  y bajamos el nueve, vemos que el
y bajamos el nueve, vemos que el  cabe una vez en el
cabe una vez en el  , sobran tres y bajamos el seis obteniendo ahora
, sobran tres y bajamos el seis obteniendo ahora  . Finalmente, tenemos que
. Finalmente, tenemos que  cabía seis veces en el
cabía seis veces en el  , por lo tanto
, por lo tanto
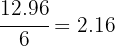
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
La suma de decimales del ejercicio 13 dan 107.82 y el resultado final es de 92.18.
Favor corregir
Hola, disculpa pero revise el ejercicio varias veces y el resultado me da 107.82, no se si podrías mencionar por que te da ese resultado.
La 5, 7 y 14 están incorrectas
Hola te agradecemos tus observaciones, pero podrías ser mas especifico en los errores pues no encontré lo que mencionas y para evitar las equivocaciones nos ayudaría mucho tus comentarios.
la 13 esta mal por los numeros. porfa corregir
Hola, una disculpa y agradecemos tu ayuda ya se corrigió.
pero finalmente el ultimo punto da 75???
Hola, podrias mencionar a qué ejercicio te refieres para contestar tu pregunta.